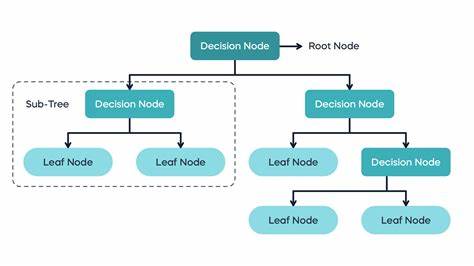
Entscheidungsbäume gehören zu den populärsten Algorithmen im Bereich des maschinellen Lernens. Obwohl sie für sich genommen gewisse Einschränkungen aufweisen, haben sie sich aufgrund ihrer Verständlichkeit und vielseitigen Einsatzmöglichkeiten einen festen Platz im Werkzeugkasten von Datenwissenschaftlern und Machine-Learning-Experten erarbeitet. Der Begriff „Entscheidungsbaum“ lässt sich leicht mit alltäglichen Entscheidungsfindungen verknüpfen: Betrachtet man die Reihe von Fragen, die man stellt, um zu einer Antwort zu gelangen, etwa ob man einen Regenschirm mitnehmen sollte – das Vorhandensein von Wolken, der Feuchtigkeitsgrad und so weiter – ähnelt dies genau der Arbeitsweise eines Entscheidungsbaums im maschinellen Lernen. Ein Entscheidungsbaum trifft eine Folge von Entscheidungen, indem er die Daten durch einzelne Fragen schrittweise in immer kleinere Gruppen einteilt. Jede Verzweigung im Baum basiert dabei auf einer Eigenschaft oder einem Merkmal der Eingangsdaten.
Dabei werden Bereiche des Merkmalsraums erstellt, die sich ungefähr auf rechteckige Abschnitte beschränken, deren Grenzen parallel zu den Achsen der jeweiligen Merkmale verlaufen. Diese Eigenschaft sorgt dafür, dass die Berechnung und Interpretation einfacher bleibt, ist jedoch gleichzeitig auch eine Einschränkung, da komplexere Muster und Zusammenhänge oft eine diagonale oder andere schräge Grenze zwischen den Klassen benötigen würden. Der Aufbau eines Entscheidungsbaums beginnt an der Wurzel, die die gesamte Menge an Trainingsdaten umfasst. Diese Daten werden anhand eines ausgewählten Merkmals und eines Grenzwertes gespalten. Für jede mögliche Aufteilung wird eine Kennzahl - auch als Kriterium oder Objektiv bezeichnet - berechnet, die die Güte der Aufteilung beschreibt.
Für Klassifikationsaufgaben werden häufig der Gini-Impurity-Index oder die Entropie verwendet, während bei Regressionsproblemen der quadratische Verlust (Mean Squared Error) als Maß der Güte dient. Im Bereich der Klassifikation wird bei jeder Frage im Baum überprüft, wie gut die Aufteilung darin besteht, eine Gruppe möglichst homogener Datenpunkte zu erzeugen, sprich Datenpunkte, die derselben Klasse angehören. Das Ziel ist es, die Unreinheit der Daten in den Blättern, also den Endpunkten des Baums, zu minimieren. Idealerweise endet die Baumstruktur bei Blättern, die nur Daten einer einzelnen Klasse umfassen, was als reiner Knoten bezeichnet wird. In der Praxis werden Bäume jedoch oft nicht bis zur maximalen Tiefe wachsen gelassen, um Overfitting zu vermeiden.
Overfitting bezeichnet das Phänomen, dass ein Modell die Trainingsdaten zwar perfekt beschreibt, aber beim Umgang mit neuen, unbekannten Daten versagt, was auf eine Überanpassung an Rauschen oder Zufälligkeiten in den Trainingsdaten zurückzuführen ist. Neben der Klassifikation kann ein Entscheidungsbaum auch als Regressor genutzt werden. In diesem Fall ist das Ziel, kontinuierliche Werte vorherzusagen, wie zum Beispiel den Preis eines Hauses basierend auf Merkmalen wie Wohnfläche, Anzahl der Zimmer oder Standort. Die Blätter eines Regressionsbaums enthalten in der Regel den Durchschnittswert der Zielvariable für die Trainingsbeispiele, die diesen Knoten erreicht haben. Ein entscheidender Vorteil von Entscheidungsbäumen ist ihre einfache Interpretierbarkeit: Jede Entscheidung kann nachvollzogen werden, da sie einer einfachen Regel folgt, was bei vielen anderen Machine-Learning-Methoden, die als Black-Box-Modelle gelten, nicht der Fall ist.
Diese Eigenschaft macht Entscheidungsbäume besonders für Anwendungen in sensiblen Bereichen wie Medizin oder Recht attraktiv, wo erklärbare Entscheidungen von großer Bedeutung sind. Die gängigsten Algorithmen zum Erstellen von Entscheidungsbäumen sind ID3, C4.5 und CART. Während ID3 für Klassifikationen mit kategorialen Merkmalen konzipiert wurde, erweitern C4.5 und CART diese Grundlagen um die Behandlung numerischer Daten und bei CART auch um Regressionsbäume.
CART (Classification and Regression Trees) setzt auf binäre Aufteilungen, das heißt, jeder Knoten teilt seine Daten genau in zwei Gruppen, was zu tendenziell höheren, aber übersichtlicheren Bäumen führt. Die mathematische Darstellung eines Entscheidungsbaums lässt sich als Summe über Regionen im Merkmalsraum auffassen. Jedem dieser Bereiche wird ein konstanter Wert oder ein Wahrscheinlichkeitsvektor zugeordnet, der die Vorhersage des Modells in diesem Bereich definiert. Die Trennungslinien verlaufen dabei immer parallel zu den Achsen der Merkmale, wodurch die Regionen rechteckige Formen annehmen. Diese Vorgehensweise ist rechnerisch effizient und erlaubt die schnelle Suche nach optimalen Trennungen durch Sortieren der Datenpunkte pro Merkmal.
Die Zeitkomplexität für die Suche nach besten Splits auf einer Dimension liegt bei O(n log n), wobei n die Anzahl der Datenpunkte ist. Hingegen ist die Suche nach obliquen, also schrägen Trennlinien immens aufwändiger und daher in der Praxis selten. Eine der Herausforderungen bei Entscheidungsbäumen liegt in der sogenannten Bias-Variance-Problematik, einem zentralen Thema in der Statistik und dem maschinellen Lernen. Entscheidungsbäume neigen dazu, entweder zu einfach zu sein (hoher Bias) und wichtige Muster in den Daten nicht zu erfassen, oder zu komplex zu werden (hohe Varianz) und sich zu stark an das Rauschen der Trainingsdaten anzupassen, was zum Overfitting führt. Typischerweise werden Techniken wie die Begrenzung der maximalen Baumtiefe, die Festlegung einer Mindestanzahl von Datenpunkten pro Blatt oder das Beschneiden (Pruning) genutzt, um den Baum zu regulieren und die Balance zwischen Bias und Varianz zu erreichen.
Trotz aller Stärken haben Entscheidungsbäume auch einige Nachteile. Insbesondere das sogenannte Treppeneffekt-Phänomen beschreibt die Schwierigkeit, glatte oder lineare Entscheidungsgrenzen mit einem Baum zu modellieren. Aufgrund der Achsen-parallelen Trennungen entstehen polygonale Bereiche, die diagonale oder gekrümmte Grenzen approximieren, was zu unstetigen Vorhersagen führt und etwa bei Regressionsaufgaben problematisch sein kann. Zudem sind Entscheidungsbäume dafür bekannt, instabil zu sein. Schon kleine Veränderungen in den Trainingsdaten können zu erheblich unterschiedlichen Baumstrukturen führen, was die Verlässlichkeit des Modells beeinträchtigt.
Dieses Problem wird allerdings durch Ensemble-Methoden wie Bagging und Boosting teilweise gelöst, bei denen viele einfache Bäume kombiniert werden, um robustere und leistungsfähigere Modelle zu schaffen. Schließlich extrapolieren Entscheidungsbäume nicht über den Bereich der Trainingsdaten hinaus. Wenn neue Daten außerhalb des gelernten Merkmalsraums liegen, werden einfach die nächstliegenden Blattvorhersagen verwendet. Dies kann in Szenarien, in denen sich Trends über beobachtete Bereiche hinaus erstrecken, zu suboptimalen Ergebnissen führen. Zusammenfassend sind Entscheidungsbäume ein sowohl leistungsstarkes als auch leicht verständliches Werkzeug des maschinellen Lernens, das besonders durch seine Transparenz und Flexibilität punktet.
Sie eignen sich für viele Problembereiche sowohl in der Klassifikation als auch in der Regression. Ihre Grenzen liegen vor allem in der Modellierung komplexer Zusammenhänge und der Stabilität. Dennoch bleiben Entscheidungsbäume, insbesondere in ihrer Kombination als Ensemble-Modelle, eine Grundlage zahlreicher moderner Anwendungen im Datenanalyse- und Machine-Learning-Bereich.