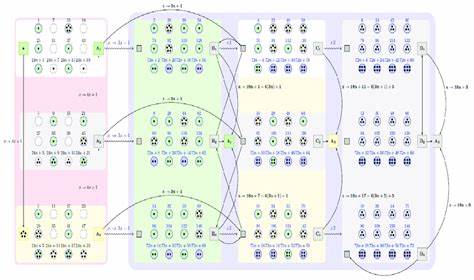
Die Collatz-Vermutung zählt zu den bekanntesten ungelösten Problemen der Mathematik und hat Forscher über Jahrzehnte fasziniert. Trotz ihrer einfachen Formulierung bleiben viele Aspekte dieser faszinierenden Folge rätselhaft. In diesem Kontext eröffnet „Collatz's Ant“ eine innovative Perspektive: eine alternative Repräsentation der Collatz-Dynamik, die auf den Prinzipien von Langton’s Ant basiert. Diese Methode erlaubt nicht nur eine visuelle Darstellung der komplexen Collatz-Landschaften, sondern ermöglicht auch neue Einsichten in ihre Struktur und Entwicklung. Collatz's Ant ist eine kreative Kombination aus der bekannten Collatz-Funktion, die Zahlenfolgen generiert, und Langton’s Ant, einem zellulären Automaten, der auf einem Gitter bestimmte Bewegungsmuster zeigt.
Statt die Collatz-Dynamik direkt in Form der Zahlenfolge zu betrachten, werden die Entwicklungen in Form von „Landschaften“ visualisiert – komplexe Gebilde auf einem Koordinatensystem, die verschiedene Aspekte der Zahlenfolge repräsentieren. Für jede natürliche Zahl n entsteht so eine einzigartige „Landschaft“, die sich aus der Betrachtung des Verhaltens von n unter der Collatz-Transformation ableitet. Ein Schlüsselaspekt bei der Analyse ist die Trajektorie, also der Weg, den die „Collatz's Ant“ durch diese Landschaft nimmt. Dabei werden Position und Winkel relativ zum Ursprung über die Zeit hinweg untersucht. Interessanterweise zeigen viele dieser Trajektorien zufallsähnliche Muster oder erinnern an random walk-Prozesse, oft mit einer eingebauten Drift, die die Bewegung in eine bestimmte Richtung lenkt.
Diese Beobachtung legt nahe, dass hinter der scheinbar chaotischen Bewegung eine verborgene Struktur steckt. Blickt man auf mehrere dieser Landschaften für unterschiedliche Startwerte n, erkennt man, dass viele davon eine gemeinsame Grundform aufweisen, obwohl sie sich durch subtile Details unterscheiden. Diese Ähnlichkeiten werfen Fragen auf: Wie genau beeinflusst die Wahl von n die Gestalt dieser Landschaften? Gibt es universelle Muster, die unabhängig von n auftauchen? Und vor allem – lässt sich die Spezifität jeder Landschaft erklären, ohne direkt auf die Collatz-Funktion Bezug zu nehmen? Die Grundidee der Methode besteht darin, zur Analyse der Collatz-Dynamik das Konzept eines reinen Zustandsraumsrarbeitens anzuwenden, analog zu dem Prinzip zellularer Automaten. Durch das Abstrahieren vom direkten Zahlenmanipulationsprozess hin zur Visualisierung der Trajektorie und Landschaft öffnet sich ein neuer Blickwinkel, der mathematische wie dynamische Eigenschaften gemeinsam betrachtet. Unter Einbeziehung von Langton’s Ant als Modell für einfache Regeln, die zu kompliziertem Verhalten führen können, entstehen seltsame Muster und Entwicklungen auf einem Gitter.
Diese analoge Herangehensweise bei Collatz's Ant macht es möglich, mathematisch und visuell die Veränderung von Position und Winkel im Laufe der Iterationen nachzuvollziehen. Dabei können unterschiedliche Verhaltensweisen beobachtet werden: von stabilen Zyklen bis hin zu scheinbar zufälligen Wanderungen. Speziell die Betrachtung von Abstand (euklidische Distanz) und Winkel (in Radiant) zu einem festen Ursprung ermöglicht eine neue Form der zeitlichen Analyse. Diese zeitlichen Verläufe geben Auskunft darüber, wie sich die Trajektorie im Raum entwickelt, ob sie sich in Regionen konzentriert oder verstreut, und wie die Rotation um den Ursprung verläuft. Solche Erkenntnisse können helfen, verborgene regelhafte Strukturen im Trajektorienverlauf zu identifizieren.
Die Frage, ob es möglich ist, die Formen der Collatz-Landschaften und deren Abhängigkeit von n vollständig ohne Bezugnahme auf die klassische Collatz-Funktion zu erklären, ist von hohem theoretischem Interesse. Es eröffnet nämlich die Möglichkeit, diese mathematischen Objekte als eigenständige dynamische Systeme zu analysieren und zu modellieren, was besonders im Bereich der komplexen Systeme und der theoretischen Informatik von Bedeutung ist. Ein weiterer Vorteil dieser Darstellung liegt in der Veranschaulichung der Vielfalt der dynamischen Verläufe. Selbst kleine Änderungen in n können die Landschaft sichtbar verändern, was die Sensitivität der dynamischen Entwicklung unterstreicht. Das wiederkehrende Auftreten ähnlicher Grundstrukturen trotz dieser Variationen weist auf zugrundeliegende Symmetrien oder invarianten Eigenschaften hin.