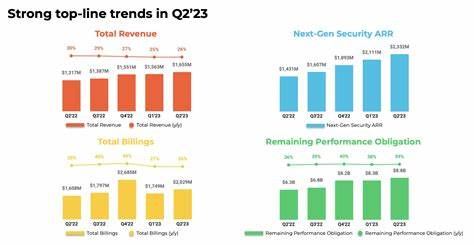
Galois-Felder, auch als endliche Körper bekannt, haben in der modernen Computerwissenschaft eine herausragende Bedeutung. Obwohl abstrakte Algebra auf den ersten Blick komplex und fern der alltäglichen Programmierpraxis erscheinen mag, sind die Konzepte hinter Galois-Feldern essenziell für viele Anwendungen rund um Datensicherheit, Fehlerkorrektur und Datenkodierung. Dieser Text widmet sich dem Ziel, Galois-Felder verständlich und praxisorientiert vorzustellen und damit eine Brücke zwischen abstrakter Mathematik und praktischer Informatik zu schlagen. Das Verständnis von Galois-Feldern beginnt bei der Erkenntnis, dass es neben den gewohnten Zahlen – wie den reellen oder ganzen Zahlen – noch andere mathematische Strukturen gibt. Diese Strukturen folgen ihren eigenen Regeln für Addition und Multiplikation, bei denen es weniger auf die konkreten Werte ankommt als auf die Beziehungen zwischen den Elementen.
Bei einem Galois-Feld handelt es sich um eine endliche Menge von Elementen, auf der Addition, Subtraktion, Multiplikation und Division (außer durch Null) definiert sind und die gewissen Axiomen folgen. Für Computerwissenschaftler ist es besonders spannend, dass Galois-Felder es ermöglichen, Operationen auf Daten so zu gestalten, dass sie innerhalb definierter Grenzen bleiben. Ein bekanntes Beispiel ist die Arbeit mit 8-Bit-Werten. In herkömmlicher Arithmetik führt eine Multiplikation zweier Bytes oft zu einem Wert, der größer als ein Byte ist. Galois-Felder erlauben es, Multiplikationen und Additionen so zu definieren, dass das Ergebnis wieder ein gültiger 8-Bit-Wert ist.
Dadurch können beispielsweise Verschlüsselungsalgorithmen oder Fehlerkorrekturverfahren effektiv umgesetzt werden. Die Herausforderung besteht oft darin, dass viele Ressourcen entweder zu abstrakt und mathematisch schwer zugänglich sind oder aber zu stark vereinfachen und dadurch nicht den praktischen Bezug herstellen, den Informatiker brauchen. Die meisten Computerwissenschaftler lernen in ihrem Studium hauptsächlich Diskrete Mathematik und lineare Algebra, aber selten tiefergehende abstrakte Algebra. Deshalb ist es wertvoll, eine Lernmethode zu haben, die Schritt für Schritt theoretische Grundlagen mit praktischen Codebeispielen verbindet. Ein solcher Ansatz fördert das aktive Lernen, bei dem Konzepte nicht nur gelesen, sondern durch praktische Übungen und implementierte Beispiele direkt erlebt werden können.
Beispielsweise können kleine Programme geschrieben werden, die mathematische Operationen in einem Galois-Feld simulieren. Diese Praxis erleichtert das Verstehen komplexer Sachverhalte und stärkt das Gefühl für die Materie. Galois-Felder sind keine reine Theorie; ihre Anwendung findet sich in vielen allgegenwärtigen Technologien. Fehlererkennung und -korrektur in digitalen Übertragungen beruhen auf diesen mathematischen Strukturen. Cyclic Redundancy Checks (CRC), die verwendet werden, um Fehler in Datenpaketen zu erkennen, basieren auf Polynomialarithmetik in Galois-Feldern.
Auch moderne Verschlüsselungsverfahren wie AES, die in sicherer Kommunikation eingesetzt werden, nutzen die algebraischen Eigenschaften dieser Felder. Ein weiteres prominentes Beispiel ist Reed-Solomon-Codierung, die in CDs, DVDs, Satellitenkommunikation und QR-Codes verwendet wird. Die Fähigkeit, Daten so zu kodieren, dass sie auch bei teilweisem Verlust rekonstruierbar sind, baut auf den Konzepten der Polynomfelder und Galois-Feldern auf. Hier wird sowohl theoretisches Wissen als auch praktische Programmierung benötigt, um die Verfahren zu verstehen und implementieren zu können. Die theoretischen Grundlagen aufzubauen bedeutet, zunächst ein Verständnis von Gruppentheorie und Körpertheorie zu erarbeiten.
Ein Galois-Feld ist ein spezieller Körper mit endlicher Elementanzahl. Dabei gilt immer, dass die Anzahl der Elemente einer Potenz einer Primzahl sein muss. Das kleinste Beispiel ist das Feld mit zwei Elementen, das oft in der Informatik für binäre Operationen eine Rolle spielt. Mit fortschreitendem Wissen werden komplexere Felder betrachtet, zum Beispiel solche mit 2^k Elementen, die speziell in der Kryptographie wichtig sind. Sprachlich ist Rust als Programmiersprache besonders geeignet, um Galois-Felder zu implementieren, weil sie sowohl hohe Leistung als auch Sicherheit bietet.
In Tutorials und Lernprojekten werden daher häufig Rust-Codebeispiele genutzt, um die mathematischen Konzepte in konkrete, lesbare und nachvollziehbare Programme zu überführen. Solche Codebeispiele helfen dabei, die Theorie greifbar zu machen und Lernende zum Mitmachen zu animieren. Der Weg zum vollständigen Verständnis von Galois-Feldern umfasst nicht nur Mathematik, sondern auch Programmierpraxis. Denkbare Themen für eine vertiefende Auseinandersetzung sind die Implementierung von verschiedenen Feldtypen, das Rechnen mit Polynomen in diesen Feldern und die Anwendung auf reale Aufgaben wie CRC oder AES-Verschlüsselung. Dabei ist es wichtig, den Fokus auf Verständlichkeit zu behalten und nicht von Beginn an auf maximale Performance zu optimieren.
So kann jeder Lernende in seinem Tempo Fortschritte machen und die abstrakte Algebra praktisch anwenden. Zusammengefasst eröffnen Galois-Felder eine faszinierende Welt, in der Mathematik und Informatik verschmelzen. Sie bilden die Grundlage für viele Technologien, die unsere digitale Kommunikation sicher und zuverlässig machen. Für Computerwissenschaftler ist es daher empfehlenswert, sich die Zeit zu nehmen, diese Konzepte Schritt für Schritt zu erlernen und mit praktischen Projekten zu vertiefen. Nur so lässt sich die oft als abstrakt empfundene Mathematik lebensnah und nutzbringend verstehen.
Die Kombination aus theoretischem Fundament und praxisorientiertem Lernen ist der Schlüssel zum Erfolg. Wer sich mit Galois-Feldern vertraut macht, erwirbt nicht nur ein solides mathematisches Wissen, sondern öffnet auch die Tür zu hochinteressanten Anwendungen in der modernen Technologie. Ob Kryptographie, Fehlerkorrektur oder Datenkodierung – die abstrahierte Welt der endlichen Körper bietet Lösungen für reale Herausforderungen in der Computerwissenschaft. Damit Computerwissenschaftler nicht von Fachjargon abgeschreckt werden, ist es hilfreich, die Inhalte so aufzubereiten, dass sie schrittweise aufgebaut werden. Vom Verständnis der grundlegenden Begriffe der Algebra bis hin zu konkreten Anwendungen mit Beispielen in Programmiersprachen wie Rust stellt ein solcher Lernpfad eine wertvolle Ressource dar.
Dies ermöglicht nicht nur theoretische Einsichten, sondern auch die Motivation, eigene Projekte zu entwickeln und das Gelernte praktisch umzusetzen. Letztlich ist es das Ziel, die Hürde abstrakter Konzepte zu überwinden und einen praxisnahen Zugang zu schaffen. Galois-Felder sind ein Schlüsselbaustein moderner Computermathematik. Mit Geduld, strukturiertem Lernen und praktischen Experimenten lassen sich diese komplexen Ideen meistern und in der täglichen Arbeit nutzbringend einsetzen.