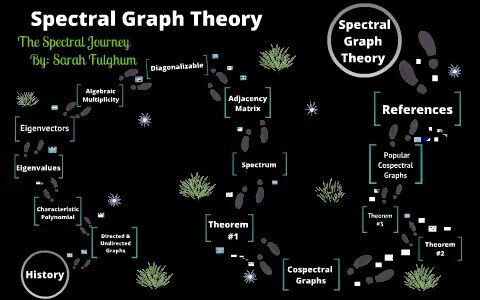
Spektralgraphentheorie ist ein bedeutendes Forschungsfeld an der Schnittstelle von Mathematik, Informatik und Ingenieurwesen, das sich mit der Analyse von Graphen anhand der Eigenwerte und Eigenvektoren ihrer zugehörigen Matrizen beschäftigt. Diese Disziplin bietet eine mächtige Methode zur Untersuchung von Eigenschaften komplexer Netzwerke und findet Anwendung in vielfältigen Bereichen wie Computernetzwerken, Physik, Soziologie, biologischen Netzwerken und Algorithmenentwicklung. Die grundlegende Idee der Spektralgraphentheorie ist, dass viele strukturelle Eigenschaften eines Graphen durch seine spektralen Charakteristika, also die Eigenwerte und Eigenvektoren der Adjazenmatrix oder der Laplace-Matrix, abgebildet werden können. Diese Spektren spiegeln beispielsweise Informationen über die Konnektivität, Cliquen, Färbungen, Schnitte oder Flüsse im Graph wider und liefern dadurch wertvolle Einsichten, die mit herkömmlichen graphentheoretischen Techniken schwer zu erlangen wären. Ein wichtiger Ausgangspunkt der Spektralgraphentheorie ist die Betrachtung der Adjazenzmatrix eines Graphen.
Diese Matrix erfasst, welche Knoten durch Kanten verbunden sind, und deren Eigenwerte geben Aufschluss über das Zusammenspiel der Knoten. Besonders bei regulären Graphen, bei denen jeder Knoten die gleiche Anzahl an Nachbarn besitzt, lassen sich mittels spektraler Techniken präzise Aussagen über deren Struktur treffen. Die Spektralgraphentheorie nutzt darüber hinaus die Laplace-Matrix, eine zentrale Konstruktion, die aus der Differenz zwischen der Grad-Matrix und der Adjazenzmatrix gebildet wird. Diese Matrix ist wesentlich für die Analyse der Algebraischen Konnektivität, welche als zweitkleinster Eigenwert der Laplace-Matrix bezeichnet wird und ein Maß für die Stärke der Verbindung des Graphen ist. Ein weiterer bedeutender Aspekt ist die Anwendung der sogenannten Cheeger-Ungleichung, die eine Brücke zwischen der graphentheoretischen Schnittgröße und dem Spektrum der Laplace-Matrix schlägt.
Diese Ungleichung ermöglicht es, durch die Analyse der Eigenwerte obere und untere Schranken für wichtige graphentheoretische Größen wie den sparsesten Schnitt im Graph aufzustellen. Durch diese Verbindung lassen sich komplexe Optimierungsprobleme im Graphen, die sonst nur schwer zu lösen sind, effektiver angehen. Im Rahmen moderner Forschung hat die Spektralgraphentheorie auch algorithmische Innovationen vorangetrieben. So hat beispielsweise Trevisan mit seinem spektralen Approximationsalgorithmus für das Max-Cut-Problem gezeigt, wie man mithilfe von Eigenwertanalyse effiziente Näherungslösungen für NP-schwere Probleme finden kann. Insgesamt zeigt sich, dass spektrale Methoden sowohl in der theoretischen Graphentheorie als auch in der praktischen Algorithmik unverzichtbar geworden sind.
Darüber hinaus finden in der Spektralgraphentheorie auch neuartige Konzepte wie die Matrix-Sparsifier und Laplacian-Solver breite Anwendung. Spectral Sparsifiers ermöglichen es, große Netze durch kleinere, spektral ähnliche Graphen zu approximieren, sodass Rechenaufwand und Speicherbedarf reduziert werden, ohne die wesentlichen Eigenschaften des ursprünglichen Graphen zu verlieren. Laplacian-Solver sind fortschrittliche Algorithmen, die lineare Gleichungssysteme in Bezug auf Laplace-Matrizen effizient lösen und damit Anwendungen wie elektrische Netzwerkanalysen und Flussprobleme ermöglichen. Die Verbindung zu elektrischen Netzwerken wird insbesondere durch das Konzept des Effektivwiderstands innerhalb eines Graphen deutlich. In diesem Zusammenhang stellt man sich die Kanten als Widerstände vor, und die Spektralgraphentheorie liefert Instrumente, um Ströme und Spannungsverteilungen über den Graphen zu modellieren.
Dadurch lassen sich Anwendungen in der Optimierung von Netzwerkflüssen, der Simulation von Diffusionsprozessen oder der Analyse dynamischer Systeme realisieren. Ein weiterer spannender Bereich innerhalb der Spektralgraphentheorie sind Random Walks auf Graphen. Hierbei analysiert man zufällige Pfade, die durch die Knoten des Graphen ziehen, wobei die spektralen Eigenschaften helfen, Fragen der Stationarität, der Mischzeit und der Konvergenzgeschwindigkeit von solchen Zufallsgängen zu beantworten. Diese Erkenntnisse sind besonders in der Informatik relevant, etwa bei der Entwicklung von Suchmaschinenalgorithmen oder in der Netzwerksicherheit. Neben der Analyse klassischer Grapheigenschaften bietet die Spektralgraphentheorie auch Einblicke in komplexere Strukturen und Invarianten, wie den Colin de Verdière-Invariant, der eine Verbindung zwischen der Graphentheorie und der Geometrie oder Topologie von Netzwerken herstellt.
Diese tiefgehenden mathematicalischen Konzepte eröffnen neue Perspektiven zur Untersuchung von Planarität, Knotentheorie und höherdimensionalen Netzwerken. Fortschritte in der theoretischen Spektralgraphentheorie führen ebenfalls zu praktischen Verbesserungen bei der Realisierung schneller Algorithmen. So haben Forscher wie Kyng und Sachdeva effiziente Algorithmen präsentiert, die es erlauben, Lösungen für Laplacian-Gleichungssysteme mit nahezu linearer Zeitkomplexität zu berechnen. Diese Entwicklungen sind bedeutsam für Anwendungen in Bereichen wie maschinelles Lernen, große Datennetzwerke, Signalverarbeitung und vieles mehr. Die Historie der Spektralgraphentheorie weist auf bedeutende Werke und Beiträge hin, angefangen bei der Matrix-Baum-Theorie, die schon früh Verbindungen zwischen Graphenstrukturen und Determinanten von speziellen Matrizen erkannte, bis hin zu den jüngsten algorithmischen Fortschritten bei der Spektralen Zerlegung von Graphen.
Lehrstühle an renommierten Universitäten bieten Kurse an, die sowohl theoretisches Wissen vermitteln als auch aktuelle Forschungsergebnisse präsentieren, was die Bedeutung des Feldes im akademischen Kontext unterstreicht. Insgesamt ist die Spektralgraphentheorie ein dynamisches und vielschichtiges Forschungsgebiet, das sowohl theoretisch als auch praktisch hohe Relevanz besitzt. Ihre Konzepte haben weitreichende Auswirkungen auf die Analyse und das Verständnis komplexer Netzwerke, helfen bei der effizienten Lösung schwieriger Optimierungsprobleme und tragen zur Entwicklung innovativer Algorithmen bei. Für jeden, der sich mit moderner Graphentheorie und deren Anwendungen auseinandersetzt, bietet das Studium der spektralen Methoden einen tiefen Einblick in die komplexen Zusammenhänge und eröffnet neue Wege im Umgang mit Netzwerken aller Art.