Effiziente Optimierung durch Vereinigung stochastischer Gradienten- und Quasi-Newton-Verfahren

In der Welt der Optimierungstechnologien nehmen stochastische Gradientenverfahren seit Langem eine Schlüsselrolle ein, vor allem wegen ihrer Effizienz bei großen Datenmengen und bei der Arbeit mit nicht-konvexen Funktionen, die in modernen maschinellen Lernanwendungen weit verbreitet sind. Während diese Methoden durch einfache Iterationen und schnelle Berechnung der Gradienten überzeugen, mangelt es ihnen oft an der Nutzung von Zusatzinformationen über die Krümmung der Zielfunktion, was ihren Konvergenzprozess verlangsamen kann. Quasi-Newton-Verfahren hingegen zeichnen sich dadurch aus, dass sie auf Basis von zweiten Ableitungen, also dem Hessian, eine bessere Abschätzung der Zielfunktion vornehmen und somit schneller und präziser zum Optimum gelangen – allerdings zu dem Preis eines hohen Rechen- und Speicheraufwands, vor allem bei großen und hochdimensionalen Datensätzen. Die Veröffentlichung von Jascha Sohl-Dickstein, Ben Poole und Surya Ganguli im Jahr 2013 bringt eine innovative Lösung, die die Vorteile beider Welten mithilfe eines einheitlichen Algorithmus vereint. Diese Methode optimiert Summen von Funktionen effizient und adressiert gleichzeitig die Herausforderungen bezüglich Rechenleistung und Speicherbedarf.

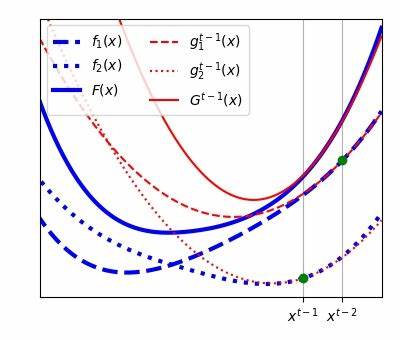
Im Kern basiert der vorgestellte Algorithmus auf der Idee, für jede Einzelkomponente der Summe eine separate Approximation der Hessian-Matrix zu errichten und diese in einem gemeinsam genutzten, sich über die Zeit entwickelnden, niedrigdimensionalen Unterraum zu speichern und zu aktualisieren. Dabei wird die Rechenlast stark reduziert, ohne auf die wertvollen Informationen zur Krümmung der Funktion verzichten zu müssen. Dieser Ansatz ermöglicht eine Skalierung auf große und hochdimensionale Optimierungsprobleme, wie sie beispielsweise in tiefen neuronalen Netzen oder anderen komplexen Modellen üblich sind. Klassische Quasi-Newton-Verfahren versuchen, das gesamte Hessian global zu approximieren, was aufgrund von Rauschen und Variabilität bei stochastischen Daten oft problematisch ist. Die Innovation der Autoren liegt darin, dass sie anstatt den lokalen Hessian-Approximationen lediglich als verrauschte Schätzungen des globalen Hessian zu sehen, diese direkt als eigenständige Ziele zur Schätzung behandeln.

Durch diese Perspektive ist das Verfahren robuster gegenüber Schwankungen in den Daten und erlaubt stabilere und gleichzeitig präzisere Updates. Ein weiterer großer Vorteil der Methode ist, dass jede Optimierungsiteration nur die Auswertung einer einzelnen Komponente der Zielfunktion oder eines kleinen Minibatches benötigt – ähnlich wie bei klassischen stochastischen Gradientenverfahren. Dadurch wird der Rechenaufwand gering gehalten, während dennoch fast sofort von den verbesserten Hessian-Informationen profitiert wird. Diese Vorgehensweise verringert nicht nur die Anzahl der nötigen Iterationen bis zur Konvergenz, sondern auch den Energieverbrauch und die Laufzeit, die gerade bei groß angelegten maschinellen Lernprojekten entscheidende Faktoren sind. Die Autoren haben die Effektivität ihres Algorithmus anhand von sieben verschiedenen Optimierungsproblemen demonstriert, die unterschiedliche Anwendungsbereiche abdecken.

Die Ergebnisse zeigen eine signifikante Beschleunigung der Konvergenz gegenüber herkömmlichen rein stochastischen oder Quasi-Newton-Verfahren. Zudem erfordert der Algorithmus wenig bis gar keine Anpassung der Hyperparameter, was die praktische Anwendbarkeit erheblich vereinfacht. Für viele Entwickler und Forscher, die bisher durch aufwendiges Hyperparameter-Tuning und Speicherbeschränkungen limitiert waren, bietet dieses Verfahren eine attraktive neue Möglichkeit, ihre Modelle schneller und zuverlässiger zu trainieren. Ein Aspekt, der in der wissenschaftlichen Gemeinschaft viel Aufmerksamkeit erregt hat, ist die Veröffentlichung des Algorithmus als Open-Source-Pakete sowohl in Python als auch in MATLAB. Dies erleichtert den Einstieg für verschiedenste Anwender und beschleunigt die Verbreitung dieser modernen Optimierungstechnik.

Die Verfügbarkeit von Quellcode und Dokumentation fördert zudem die Weiterentwicklung durch die Gemeinschaft und die Integration in bestehende maschinelle Lernbibliotheken. Insgesamt steht dieser Ansatz exemplarisch dafür, wie durch die geschickte Kombination etablierter Methoden neue Synergien entstehen können, die bisherige Limitationen überwinden und entscheidende Verbesserungen bei der Lösung komplexer mathematischer Probleme ermöglichen. Die Verbindung von schnelle, stochastisch-getriebenen Gradientenverfahren mit der präzisen, zweiter Ordnung basierenden Quasi-Newton-Methode schafft eine leistungsstarke Optimierungsstrategie, die in Zukunft in vielen Bereichen der KI, Datenwissenschaft und numerischen Mathematik Anwendung finden wird. Wer sich mit modernen Algorithmen zur Optimierung beschäftigt, sollte daher den innovativen Ansatz von Sohl-Dickstein und Kollegen kennen und prüfen, wie sich die Methode in eigenen Projekten einsetzen lässt, um bessere und schnellere Ergebnisse zu erzielen.