Die Peano-Arithmetik bildet das Fundament moderner Zahlentheorie und Mathematik, indem sie die natürlichen Zahlen anhand weniger einfacher, aber präziser Axiome definiert. Trotz ihrer scheinbaren Einfachheit eröffnen diese Axiome einen Zugang zu den komplexen Operationen der Arithmetik – allen voran Addition und Multiplikation. Dabei wird gerade die Multiplikation häufig in der Schule als „wiederholte Addition“ vermittelt. Doch eine tiefere mathematische Betrachtung zeigt, dass der Zusammenhang weit subtiler ist. Entscheidend für das Verständnis ist das sogenannte Rekursionsprinzip, das es erlaubt, Funktionen wie Addition und Multiplikation strikt und wohlbegründet aus den Peano-Axiomen heraus zu definieren.
Diese Definitionen basieren nicht auf bloßer Wiederholung, sondern auf einem formalen Konstrukt, das den Übergang vom Endlichen zum Unendlichen mathematisch abgesichert vollzieht. Die Peano-Axiome definieren die natürlichen Zahlen als ein System, das eine Null (oder eine als Startzahl definierte natürliche Zahl) sowie einen Nachfolgeroperator besitzt. Mit dieser Grundstruktur lassen sich Zahlen nacheinander erzeugen und insbesondere die Induktion formulieren, ein zentrales Prinzip, um Aussagen über alle natürlichen Zahlen zu beweisen. Doch um arithmetische Operationen zu definieren, benötigt man mehr als nur die pure Existenz der Zahlen und ihrer Nachfolger. Es braucht eine Methode, mit der Funktionen auf diesen Zahlen eindeutig konstruiert werden können.
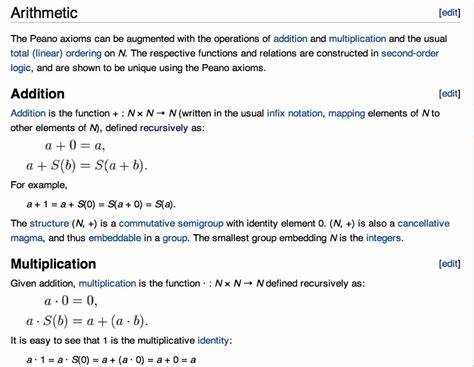
Genau hier kommt das Rekursionsprinzip ins Spiel. Das Rekursionsprinzip gewährt die Existenz und Eindeutigkeit solcher rekursiv definierten Funktionen, die auf den natürlichen Zahlen operieren. Vereinfacht betrachtet, erlaubt es, eine Funktion F zu definieren, indem man ihren Wert für eine Startzahl festlegt und anschließend ihre Werte für alle anderen Zahlen in Bezug auf vorherige Werte beschreibt. Beispielsweise wird bei der Addition die Funktion so definiert, dass das Addieren einer Zahl mit null diese Zahl ergibt, und das Addieren mit dem Nachfolger einer Zahl durch Anwendung des Nachfolgeroperators auf das Ergebnis der vorherigen Addition charakterisiert wird. Für die Multiplikation funktioniert es analog, nur dass diese nun auf der bereits definierten Addition aufbaut, statt auf dem Nachfolgeroperator.
Genauer gesagt wird die Multiplikation in der Peano-Arithmetik als eine Funktion M definiert, die zwei natürliche Zahlen a und b nimmt und das Produkt von a und b liefert. Dabei gilt zunächst, dass das Produkt mit null immer null ist. Für die Nachfolgerzahl von b definiert man das Produkt als die Summe von a und dem Produkt von a mit b. Formal lässt sich das so schreiben: M(a,0) = 0 und M(a,S(b)) = P(a,M(a,b)), wobei P die Addition ist und S der Nachfolgeroperator. Diese Definition ist eine rekursive Funktion, deren Existenz und Eindeutigkeit vom Rekursionsprinzip abgesichert wird.
Wichtig ist, dass diese rekursive Definition nicht einfach bedeutet, dass Multiplikation „wiederholte Addition“ ist. Vielmehr ist die Multiplikation eine eigenständige Funktion, die zwar durch die Addition definiert wird, aber nicht nur aus einer Reihe von Additionensschritten besteht. Die Rekursion erlaubt es, die Funktion abstrakt zu definieren, ohne auf eine einfache Interpretation im Sinne von wiederholter Addition angewiesen zu sein. Im mathematischen Sinne kann man sagen, die Multiplikation ist eine Funktion, die gemäß dem Rekursionsprinzip konstruiert wird, und ihre Berechnung für konkrete Zahlenwerte gelingt durch iterative Anwendung der zugrundeliegenden Operationen – doch die Funktionsdefinition bleibt fundamental verschieden von einem bloßen Wiederholungsprozess. Viele Lehrmaterialien greifen auf vereinfachte Darstellungen zurück und veranschaulichen Multiplikation in den frühen Lernphasen als wiederholte Addition.
Das ist für das intuitive Verständnis junger Lernender nützlich und pädagogisch nachvollziehbar. Dennoch weist die formale Mathematik darauf hin, dass beim Übergang zu höherem mathematischem Denken und zum Verständnis fundamentaler Konzepte, wie sie in der Peano-Arithmetik formuliert werden, dieses einfache Bild nicht ausreichend ist und sogar irreführend sein kann. Denn die Peano-Arithmetik setzt auf strikte Definitionen und Logik statt Intuition. Das trägt dazu bei, die mathematischen Grundlagen zu sichern und Konsistenz sowie weitere Entwicklungen zu ermöglichen. Die strukturelle Bedeutung der Multiplikation in der Peano-Arithmetik geht über bloße Rechenregeln hinaus.
Die Operation ist beispielsweise notwendig, um fortgeschrittene mathematische Konzepte wie Primzahlen, Teilbarkeit oder die Entwicklung von Zahlentheorie zu formulieren und zu beweisen. Die Rekursionsprinzipien, die ihr zugrunde liegen, bilden daher eine Brücke zwischen elementarem Zählen und komplexen mathematischen Strukturen. Ohne dieses Prinzip wäre die Konstruktion von arithmetischen Funktionen in der Mathematik, so wie wir sie heute kennen, nicht möglich. Die Rekursion ist dabei mehr als das bloße Wiederholen. Sie ist ein abstraktes Prinzip, das die Bildung von Funktionen auf unendlich vielen natürlichen Zahlen erlaubt, also die Weiterführung mathematischer Operationen vom Endlichen ins Unendliche.
In gewisser Weise ist sie ein mächtiges Werkzeug, das es Mathematikern erlaubt, auf formaler Basis Operationen zu definieren, die intuitiv vor allem aufgrund von endlichen Erfahrungswerten erschlossen werden, wie das Zählen oder einfache Addition. Darum ist es relevant zu betonen, dass das formale Konzept der Multiplikation in der Peano-Arithmetik dem mathematisch rigorosen Aufbau von Zahloperationen dient. Es verdeutlicht die Trennung zwischen intuitiver Vorstellung und formaler Definition. Den Schritt von der intuitiven Vorstellung „Multiplikation ist wiederholte Addition“ hin zur axiomatischen Definition macht man erst, wenn eine unabdingbare formale Grundlage geschaffen werden soll, die für alle weiteren mathematischen Entwicklungen tragfähig ist. Der Einsatz des Rekursionsprinzips hat zudem weitreichende Konsequenzen für die Mathematik als Ganzes.
Es ist Teil der axiomatischen Basis, die sicherstellt, dass sich Begriffe wie Addition und Multiplikation eindeutig definieren lassen und dieselben Eigenschaften erfüllen, die wir ihnen intuitiv zuschreiben, ohne dabei auf konkrete Rechenvorgänge angewiesen zu sein. Das gibt Mathematikern die Sicherheit, dass ihre Operationen konsistent bleiben, auch wenn sich das mathematische Universum ausdehnt und komplexer wird. Es ist auch interessant, das Missverständnis aufzugreifen, dass Multiplikation lediglich eine Erweiterung der Addition durch simples Wiederholen sei. Tatsächlich liegt die Differenz nicht nur im formaleren Rahmen, sondern auch in der Natur der Operationen selbst. Addition ist eine grundlegende Art des Zusammenzählens, während die Multiplikation eine strukturiertere Verbindung von Zahlen darstellt, die auf anderen logischen Beziehungen basiert und zahlreiche weitere mathematische Eigenschaften mit sich bringt.
Nicht zuletzt zeigt die detaillierte Untersuchung der Definition von Multiplikation in der Peano-Arithmetik, wie außergewöhnlich die formale Mathematik im Vergleich zur alltäglichen Anschauung ist. Sie ist das Ergebnis jahrhundertelanger Bemühungen, den Bereich der Zahlen und ihrer Operationen nicht nur praktisch anwendbar, sondern auch theoretisch vollkommen konsistent und nachvollziehbar zu machen. Das Verständnis dieser Grundlagen bietet Einblick in das Wesen der Mathematik als Wissenschaft, die über bloße Mustererkennung hinausgeht und die Strukturen des Unendlichen greifbar macht. Insgesamt lässt sich festhalten, dass die Multiplikation in der Peano-Arithmetik durch ein streng definiertes rekursives Verfahren entsteht, das die Existenz und Eindeutigkeit der Operation sichert. Dieses Verfahren stellt eine Grundlage dar, auf der die komplexe Welt der Zahlen und Zahloperationen aufbaut.
Damit wird die Multiplikation zu einem mathematischen Konzept, das weit über die einfache Idee der wiederholten Addition hinausweist und das Verständnis von Zahlen auf ein neues Level hebt.