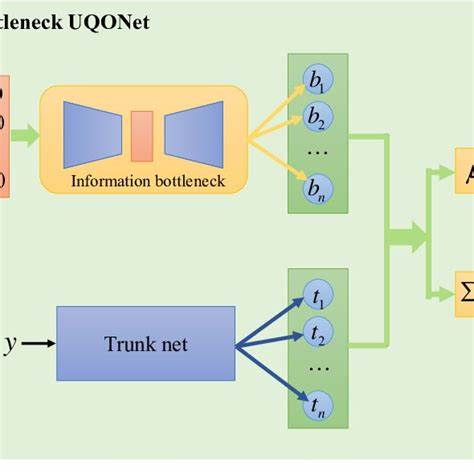
Das Information Bottleneck (IB) Framework ist seit vielen Jahren ein zentrales Forschungsgebiet in der Informationswissenschaft und dem maschinellen Lernen. Es beschäftigt sich mit der optimalen Kompression von Informationen unter Beibehaltung relevanter Eigenschaften für eine Zielvariable. In letzter Zeit stieß insbesondere die Optimierung des sogenannten β-Parameters auf großes Interesse. Dieses β steuert den Trade-off zwischen Informationskompression und Bewahrung wichtiger Merkmale. Ein hochkomplexes Problem dabei sind sogenannte Phasensprünge – abrupte Übergänge, die mathematische Optimierung erschweren und für Instabilitäten sorgen.
Hier setzt eine neue, konvexifizierte Methode an, die diese Schwierigkeiten adressiert und den Rechenprozess deutlich stabiler gestaltet. Die konvexifizierte Information Bottleneck Optimierung basiert auf einem innovativen mathematischen Ansatz, der im Kern die herkömmliche nichtkonvexe Problemstellung in eine konvexe Form verwandelt. Diese Transformation ermöglicht es, dass starke mathematische Werkzeuge und Algorithmen der konvexen Optimierung eingesetzt werden können, was zu deutlich robusterer und vor allem stabilerer Ergebnisfindung führt. In der Praxis werden dadurch typische Probleme wie das Verharren in lokalen Minima oder sprunghafte Phasenwechsel vermieden – was als Phasensprünge bekannt ist. Zugleich implementiert der neue Solver einen sogenannten Prädiktor-Korrektor-Algorithmus.
Dabei handelt es sich um eine fortschrittliche Technik zur numerischen Behandlung von Differentialgleichungen, die hier genutzt wird, um den Verlauf des β-Parameters stetig und kontrolliert zu verfolgen. Die Kontinuität der Lösungspfade gewährleistet eine nahtlose Anpassung der Informationskompressionseigenschaften ohne abrupte Sprünge – ein elementarer Fortschritt für präzise Systemanalysen. Technologisch zeichnet sich das neue Verfahren durch die Integration eines kleinen Entropie-Regulators aus, der als Zusatzterm in die Optimierungsfunktion einfließt. Dieser Regulator stabilisiert die Lösungskurve zusätzlich und unterstützt die Überführung des Ausgangsproblems in seinen konvexen Surrogatzustand. Dadurch profitierte das Framework nicht nur von mathematischer Eleganz, sondern im Wesentlichen auch von einer verbesserten numerischen Robustheit und Verlässlichkeit.
Die im Rahmen dieses Ansatzes verwendeten Werkzeuge und Bibliotheken setzen auf moderne Python-Technologien mit Schwerpunkt auf leistungsfähigen Bibliotheken wie NumPy, SciPy und JAX. JAX sorgt dabei für effiziente Berechnungen und ermöglicht optional den GPU-Einsatz, was besonders für große oder hochdimensionale Datenaufgaben relevant ist. Das zugrundeliegende Repositorium bietet drei Hauptversionen des Codes: eine initiale Validierungsframework-Version, eine Multi-Pfad-Inferenz mit Verbesserungen bei der Stabilität und schließlich die aktuelle Version mit stabiler und konvexifizierter Fortsetzung, die all diese Elemente optimal kombiniert. Die evolutionäre Entwicklung der Codebasis verdeutlicht die zunehmende Komplexität und Robustheit des Frameworks. Die allererste Version fokussierte sich auf die Validierung eines kritischen β-Werts mit Hilfe symbolischer Berechnungen.
Die darauf folgende Version integrierte inkrementelle Schritte und Multi-Pfad-Erweiterungen, um Einbrüche in der Kodierung zu verhindern und robuste Lösungen über ein breiteres β-Spektrum zu garantieren. Die aktuellste Version setzt final an den Schwächen vorangegangener Ansätze an, beseitigt Phasensprünge vollständig und verwendet ein neues Präzisionslevel durch 64-Bit Berechnung mit JAX, um sowohl Stabilität als auch Genauigkeit zu gewährleisten. Das Framework hat sich als besonders leistungsstark in einem klassischen Testumfeld behauptet, nämlich der Polarisation von Informationspfaden durch den sogenannten binären symmetrischen Kanal (BSC). Hier und im Kontext von 8×8-Kanälen konnte die Methode die entscheidenden Phasenübergänge präzise, kontinuierlich und reproduzierbar abbilden. Das Ergebnis sind durchgängig glatte Informationskurven im sogenannten Informationsplan, was eine verbesserte Interpretierbarkeit und Analyse des Datenflusses besonders in komplexen neuronalen Netzwerken bedeutet.
Ein weiterer bedeutender Vorteil des konvexifizierten IB-Ansatzes ist die erweiterte Fähigkeit zur Detektion und Behandlung von Bifurkationen. Solche Bifurkationen repräsentieren kritische Punkte, an denen sich Lösungsstränge aufspalten oder zusammenlaufen können. Die neue Methodik überwacht diese Schlüsselstellen mittels Hessischer Eigenwert-Analyse und passt über den Prädiktor-Korrektor-Mechanismus fortlaufend die Parameterführung an. Diese Präzision erhöht die Transparenz und Kontrolle im Systemverhalten erheblich. Für Forscher und Praktiker bedeutet die Anwendung dieser verbesserten IB-Optimierung nicht nur eine erhöhte Genauigkeit, sondern auch eine bedeutende Vereinfachung im Umgang mit komplexen und mehrdimensionalen Datensätzen und Modellen.
Besonders im Bereich der maschinellen Informationskompression, der Merkmalextraktion und der effizienten Datenrepräsentation eröffnet der Ansatz neue Perspektiven. Ausblickend plant der Entwickler Faruk Alpay mit der angekündigten vierten Version eine noch umfassendere Erweiterung. Geplant sind eine vollständige formale Beweisführung für globale Konvexität und Eindeutigkeit der Lösungen sowie eine adaptive Entropieplanung in Abhängigkeit von der Hessischen Konditionszahl. Zusätzlich sollen größere Datensätze, darunter klassische Bilderkennungsszenarien wie MNIST und CIFAR-10, als Demonstrationsfelder für die Leistungsfähigkeit der Methode hinzukommen. Mit der Einführung eines Paket-Managements via PyPI und einer Benutzeroberfläche für CLI wendet sich das Projekt auch an ein breiteres Publikum.
Neben den technischen Details ist der wissenschaftliche Impact ebenfalls bemerkenswert. Die Arbeit wurde auf arXiv veröffentlicht und steht unter einer nicht-exklusiven Verbreitungslizenz, um die Weiterverbreitung und Nutzung zu fördern. Die Kombination aus theoretischer Analyse, Algorithmusentwicklung und praktischen Experimenten macht sie zu einer wichtigen Referenz im Bereich der Informationskompression und der deterministischen Optimierung von IB-Parametern. Abschließend betrachtet setzt der konvexifizierte Information Bottleneck Ansatz neue Standards bei der Interpretation und Optimierung informatorischer Zusammenhänge in datengetriebenen Systemen. Durch die Eliminierung bisheriger Hindernisse wie Phasensprüngen und Encoder-Kollaps bietet die Lösung eine stabile, präzise und skalierbare Grundlage für weiterführende Forschung und praktische Anwendungen.
Die Integration moderner Programmiertechnologien und fortschrittlicher mathematischer Methoden sichert die Zukunftsfähigkeit dieses Verfahrens und positioniert es als zentralen Baustein für kommende Innovationszyklen im Datenmanagement und der künstlichen Intelligenz.