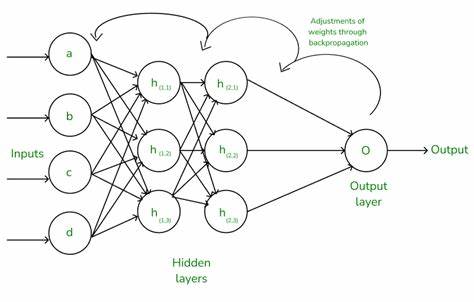
Neuronale Netze sind in der heutigen Welt des maschinellen Lernens allgegenwärtig. Sie ermöglichen eine Vielzahl von Anwendungen, angefangen bei der Bilderkennung bis hin zur Sprachverarbeitung. Doch wie genau lernen diese Netze eigentlich? Die Antwort darauf liegt in einem fundamentalen Verfahren namens Backpropagation – einem Lernalgorithmus, der es neuronalen Netzen erlaubt, ihre Vorhersagen zu verbessern. Viele Erklärungen hierzu setzen auf komplizierte mathematische Konzepte wie die Kettenregel aus der Differenzialrechnung, was den Einstieg erschweren kann. In dieser Einführung wird die Backpropagation verständlich und intuitiv erklärt, ganz ohne den Einsatz der Kettenregel.
So erhalten Sie eine solide Basis, um die Mechanik hinter dem Lernen von neuronalen Netzen zu verstehen und später komplexere Modelle leichter zu begreifen. Starten wir mit der grundlegenden Idee, warum und wie neuronale Netze lernen. Vereinfacht gesagt, sucht das Netz nach Möglichkeiten, seine Fehler zu minimieren – es versucht also, die Differenz zwischen seinen Vorhersagen und den tatsächlichen Ergebnissen gering zu halten. Das wird durch sogenannte Gewichte ermöglicht, die den Verbindungen im Netz zugeordnet sind. Beim Training werden diese Gewichte Schritt für Schritt angepasst, um die Genauigkeit der Vorhersage zu steigern.
Zur Veranschaulichung betrachten wir zunächst ein äußerst einfaches System ohne versteckte Netzwerkschichten. Stellen Sie sich vor, ein Netzwerk besteht aus nur einem einzigen Eingangswert und einem Gewicht, das diesen Eingang moduliert, um die Vorhersage zu generieren. Nehmen wir an, der Eingangswert beträgt 2, das Gewicht ist 4 und das gewünschte Zielergebnis liegt bei 10. Das Netzwerk berechnet seine Vorhersage durch Multiplikation des Eingangs mit dem Gewicht und erhält einen Wert von 8. Das bedeutet, die Vorhersage liegt 2 Einheiten unter dem Ziel.
Die zentrale Frage lautet nun: Wie verändern wir das Gewicht, um den Fehler zu reduzieren? Um dies herauszufinden, untersucht man, wie die Veränderung des Gewichts den Fehler verändert – also die Ableitung des Fehlers in Bezug auf das Gewicht. Die Ableitung zeigt an, wie empfindlich der Fehler auf Änderungen des Gewichts reagiert. Wenn die Ableitung einen Wert von 2 hat, bedeutet das, jede Erhöhung des Gewichts um 1 verringert oder vergrößert den Fehler um 2. In unserem Fall ist der Fehler negativ, was sagt, dass das Gewicht erhöht werden sollte, um den Fehler zu verringern. Erhöhen wir das Gewicht von 4 auf 5, verändert sich die Vorhersage entsprechend auf 10, sodass der Fehler verschwindet.
Dieses Vorgehen zeigt die essenzielle Rolle der Ableitung für das Lernergebnis: Sie entfaltet, in welcher Richtung und mit welcher Stärke das Gewicht angepasst werden muss. Wollen wir das Konzept etwas erweitern, fügen wir dem neuronalen Netz eine versteckte Schicht hinzu. Jetzt gibt es zwei Gewichte: eins zwischen dem Eingang und der versteckten Schicht, sowie eins zwischen der versteckten Schicht und der Ausgabe. Angenommen, der Eingang bleibt 2, das erste Gewicht ist 4 und das zweite Gewicht 3, während das Ziel weiterhin 10 ist. Das Netzwerk berechnet die Vorhersage, indem es zuerst den Eingang mit dem ersten Gewicht multipliziert und das Ergebnis dann mit dem zweiten Gewicht multipliziert, also (2×4)×3 = 24.
Der Fehler beträgt somit 14 – deutlich größer als zuvor. Um zu verstehen, wie die Gewichte angepasst werden sollen, berechnen wir die Ableitungen des Fehlers in Bezug auf beide Gewichte. Für das erste Gewicht entspricht die Ableitung dem Produkt des Eingangs mit dem zweiten Gewicht, also 2 × 3 = 6. Für das zweite Gewicht ist es die Multiplikation des Eingangs mit dem ersten Gewicht, also 2 × 4 = 8. Die höhere Ableitung beim zweiten Gewicht zeigt an, dass Änderungen an diesem größeren Einfluss auf den Fehler haben.
Wenn wir nun die Gewichte anpassen möchten, ist es nicht ratsam, die Werte abrupt zu verändern. Stattdessen wird jede Anpassung mit einem sogenannten Lernrate-Faktor multipliziert, der eine kleine Zahl ist, wie 0,01. Das sorgt dafür, dass das Lernen kontrolliert und stabil bleibt, anstatt chaotisch hin und her zu springen, was man als Explodieren des Gradienten bezeichnet. Durch wiederholtes Anpassen der Gewichte über viele Trainingsläufe hinweg nähert sich das Netzwerk seinem Ziel an und verbessert seine Vorhersagen. Das faszinierende an dieser Methode ist, dass trotz der vermeintlich einfachen mathematischen Konzepte komplexe und leistungsstarke Lernprozesse entstehen.
Manche Erklärungen verwenden die Kettenregel aus der Differentialrechnung, um die Ableitungen in komplexeren Netzwerken zu berechnen. Wir haben uns entschieden, darauf zu verzichten und die Kernidee durch direkte Anwendung der Ableitungen an einfachen Beispielen zu verdeutlichen, um die Prinzipien besser zugänglich zu machen. Wenn Sie die Mechanik der Backpropagation auf dieser grundlegenden Ebene durchblicken, fällt es Ihnen später viel leichter, die formalen Herleitungen nachzuvollziehen. Außerdem gewinnen Sie eine praktische Intuition dafür, wie sich Änderungen an Parametern im Netzwerk auf die Vorhersage auswirken. Die Erkenntnis, dass kleine und gezielte Anpassungen der Gewichte das Lernen vorantreiben, ist zentral für das Verständnis moderner künstlicher Intelligenz.
Den Lernerfolg eines neuronalen Netzes verbessern Sie zudem, indem Sie den Lernprozess sorgfältig überwachen und gegebenenfalls die Lernrate anpassen. Ist die Lernrate zu groß, kann das zu instabilem Lernen führen, während eine zu kleine Lernrate den Prozess unnötig verlangsamt. Dieses Austarieren ist Teil des Handwerks beim Aufbau und Training von Netzen. Zusammenfassend lässt sich sagen, dass Backpropagation – die Rückwärtsübertragung des Fehlers zur Anpassung der Gewichte – einfacher verstanden werden kann, als es oft dargestellt wird. Durch den Verzicht auf komplizierte mathematische Techniken wie die Kettenregel kann man mit praxisnahen Beispielen den Lernprozess begreifbar machen und Schritt für Schritt Vertrauen in die Funktionsweise neuronal gesteuerter Modelle entwickeln.
Wer sich auf diese Weise ein solides Fundament schafft, kann mit Zuversicht tiefere Ebenen der Theorie erkunden und anspruchsvollere Modelle trainieren. Vielleicht macht genau diese Art des intuitiven Lernens das komplexe Thema Backpropagation zugänglicher und motiviert, neues Wissen praxisorientiert umzusetzen.