Wavelet-Bäume: Effiziente Datenstruktur für schnelle Suche und Kompression in Sequenzen

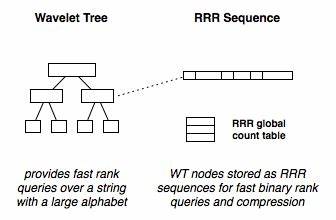
In der Welt der Datenverarbeitung und Algorithmik gewinnen effiziente Methoden zur Speicherung und Abfrage von Daten eine immer bedeutendere Rolle. Insbesondere bei der Arbeit mit großen Sequenzen über umfangreiche Alphabete, wie sie in Texten, Genomen oder anderen Datenquellen vorkommen, sind klassische Ansätze oft zu langsam oder benötigen zu viel Speicher. Eine elegante Lösung für diese Herausforderung bietet die Datenstruktur der Wavelet-Bäume, die in den letzten Jahrzehnten stetig an Relevanz gewonnen hat. Die Wavelet-Bäume stellen eine Kombination aus Baumstrukturen und komprimierten Bitvektoren dar und ermöglichen schnelle Zugriffe auf Positionen und Häufigkeiten bestimmter Symbole in einer Sequenz. Die Basisidee ist es, komplexe Alphabete durch eine binäre Zerlegung schichtweise zu repräsentieren und so rank- und select-Anfragen effizient abzuhandeln.

Wavelet-Bäume wurden erstmals 2003 von Grossi, Gupta und Vitter eingeführt und haben sich seitdem als fundamentale Technik in der Informationsverarbeitung etabliert. Durch die Einbindung von Strukturen wie den RRR-Sequenzen (benannt nach Raman, Raman und Rao) für Bitvektoren lassen sich Speicherbedarf und Zugriffsgeschwindigkeit optimal ausbalancieren. RRR-Sequenzen bieten eine schnelle Möglichkeit für bitweise Rangabfragen mit geringer Speicherbelegung, was die gesamte Wavelet-Baum-Struktur besonders kompakt und performant macht. Kern der Wavelet-Bäume ist eine hierarchische Zerlegung des Alphabets der zugrundeliegenden Sequenz. Dabei wird das Alphabet auf jeder Ebene in zwei Hälften geteilt und die Symbole entsprechend mit Bits 0 oder 1 kodiert.

Diese Kodierung wird an jedem Knoten des Baumes in Form eines Bitvektors gespeichert. Auf diese Weise kann eine Anfrage, wie etwa die Bestimmung, wie oft ein bestimmtes Symbol bis zu einer Position in der Sequenz vorkommt (rank-Query), durch eine Abfolge von rank-Abfragen auf den Bitvektoren entlang eines Pfades im Baum beantwortet werden. Trotz der anfänglichen Mehrdeutigkeit auf höheren Ebenen verliert sich diese mit fortschreitender Baumtiefe, so dass auf den Blättern eine eindeutige Zuordnung zu einzelnen Symbolen möglich ist. Der Aufbau eines Wavelet-Baumes erfolgt rekursiv. Zunächst wird das Alphabet der gesamten Zeichenfolge bestimmt und in zwei Gruppen geteilt.

Auf der obersten Ebene werden alle Symbole in zwei Klassen eingeteilt und als Bits 0 und 1 dargestellt, wodurch ein Bitvektor entsteht, der für jede Position in der Sequenz angibt, welcher Gruppe das jeweilige Symbol angehört. Anschließend wird für jede Gruppe ein Unterbaum generiert, indem jeweils die Symbole der Teilmenge erneut halbiert und in Bitvektoren kodiert werden. Dieser Prozess wird wiederholt, bis die Blätter des Baumes nur noch eine oder zwei Symbole enthalten, wodurch die Kodierung eindeutig wird. Eine der wesentlichen Stärken von Wavelet-Bäumen liegt in ihrer Fähigkeit, rank-Abfragen auf großen Alphabete mit logarithmischem Aufwand in Bezug auf die Alphabetsgröße zu beantworten. Dabei ist der zeitliche Aufwand für eine solche Abfrage proportional zu log_2(A), wobei A die Anzahl der unterschiedlichen Symbole im Alphabet darstellt.

Die Komplexität der Operationen ist somit unabhängig von der Länge der Sequenz selbst, was gerade bei sehr großen Eingabedaten von enormem Vorteil ist. Die eingesetzten rank-Abfragen auf den Bitvektoren können durch RRR oder ähnliche Strukturen in konstanter Zeit ausgeführt werden, was die gesamte Abfrage sehr performant gestaltet. Neben rank gibt es auch select-Operationen, die die Position eines bestimmten Vorkommens eines Symbols in der Sequenz ermitteln. Auch diese können auf Wavelet-Bäumen effizient implementiert werden, wenngleich die Implementierung und theoretische Erklärung oft komplexer sind. Solche Abfragen erweitern die Funktionalität der Wavelet-Bäume und ermöglichen vielfältige Anwendungen, beispielsweise in Textindizes, Kompression oder Bioinformatik.

Ein illustriertes Beispiel macht die Funktionsweise greifbar: Betrachten wir die Zeichenfolge eines bekannten Zitates, bei der die erlaubten Zeichen – inklusive Leerzeichen und Sonderzeichen – als Alphabet dienen. Auf der obersten Ebene werden die Symbole in zwei Gruppen unterteilt, repräsentiert durch 0 und 1 im Bitvektor. Die Positionen in der Eingabe werden entsprechend codiert. Für eine rank-Abfrage, etwa wie oft ein bestimmter Buchstabe bis zur fünften Position vorkommt, wird dieser Buchstabe auf jeder Ebene seinem Bit zugeordnet und die rank-Anfrage auf den korrespondierenden Bitvektor ausgeführt. Die Ergebnisse führen sukzessive über die Ebenen zu der exakten Häufigkeit an der interessierenden Stelle.

Wichtig ist zu verstehen, dass die Symbole an unterschiedlichen Baumebenen unterschiedliche Kodierungen erhalten können – eine flexible, kontextabhängige Repräsentation, die in ihrer Gesamtheit eine verlustfreie Kompression ermöglicht. Gerade in Kombination mit den RRR-Sequenzen profitieren Wavelet-Bäume nicht nur von einer effizienten Abfragegeschwindigkeit, sondern auch von einer signifikanten Einsparung beim Speicherbedarf. Besonders bei Daten mit hoher Wiederholung oder besonderer Struktur ist dieser Effekt stark spürbar. Die Einsatzmöglichkeiten von Wavelet-Bäumen sind breit gefächert. Besonders in der Textsuche, etwa bei der Implementierung von FM-Indizes oder Suffixarrays, spielen sie eine Schlüsselrolle.

Suchalgorithmen, die Muster in Texten erkennen wollen, können durch Wavelet-Bäume deutlich beschleunigt werden, da die Positionen und Häufigkeiten von Zeichen sehr schnell bestimmt werden können, ohne die gesamte Eingabesequenz durchlaufen zu müssen. Diese Effizienz macht Wavelet-Bäume zu einem unverzichtbaren Werkzeug in modernen Suchtechnologien und Datenkompressionsverfahren. Darüber hinaus finden Wavelet-Bäume Anwendung in der Bioinformatik, wo riesige Genomdatensätze analysiert werden müssen. Die Fähigkeit, große Alphabete kompakt zu verwalten und schnelle Abfragen zu ermöglichen, bringt deutliche Vorteile bei der Verarbeitung genetischer Sequenzen, die oft aus umfangreichen Symbolmengen bestehen. Die Kombination von Laufzeit- und Speicheroptimierung hilft dabei, komplexe Analysen auch auf handelsüblicher Hardware durchzuführen.

Neben der klassischen, ausgewogenen Baumform existieren auch Varianten wie der Huffman-Shaped Wavelet-Baum, der auf der Frequenzverteilung der Symbole basiert und weitere Verbesserungen bei der Kompression ermöglicht. Solche Varianten zeigen das Potential der Wavelet-Bäume, sich an spezifische Anforderungen und Datentypen anzupassen und in verschiedenen Szenarien optimal zu performen. Für Entwickler und Wissenschaftler gibt es bereits fertige Implementierungen von Wavelet-Bäumen, etwa in der Compressed Data Structure Library (libcds) von Francisco Claude. Diese Bibliotheken bieten bewährte und optimierte Lösungen, die sofort einsatzbereit sind und die Umsetzung eigener Projekte deutlich vereinfachen. Gleichzeitig bieten Wavelet-Bäume reichlich Raum für eigene Experimente und Erweiterungen etwa im Bereich der select-Abfragen oder hybriden Kompressionsverfahren.

Zusammenfassend sind Wavelet-Bäume eine elegante und effiziente Datenstruktur, die komplexe Operationen auf großen Sequenzen über umfangreiche Alphabete mit vergleichsweise geringem Aufwand ermöglicht. Durch die Kombination aus binärer Zerlegung, Bitvektoren und kompakten Rangdatenstrukturen bieten sie sowohl theoretische als auch praktische Vorteile. Ihren Einsatz finden sie in Bereichen wie der Textsuche, Bioinformatik, Datenkompression und darüber hinaus. Das tiefergehende Verständnis dieser Struktur eröffnet spannende Möglichkeiten, um Speicherressourcen optimal zu nutzen und schnelle Datenabfragen zu gewährleisten. Die Beschäftigung mit Wavelet-Bäumen lohnt sich für Informatiker, Datenwissenschaftler und Entwickler gleichermaßen – sie vermittelt Einblicke in moderne Techniken der Informationskompression und Algorithmik und stellt zugleich Werkzeuge bereit, die in vielen realen Anwendungen Mehrwert schaffen.

Wer neugierig geworden ist, sollte sich tiefer in die Literatur einlesen und praktische Implementierungen ausprobieren, um die vielfältigen Einsatzpotenziale und die Schönheit dieser Datenstruktur vollständig zu erfassen.