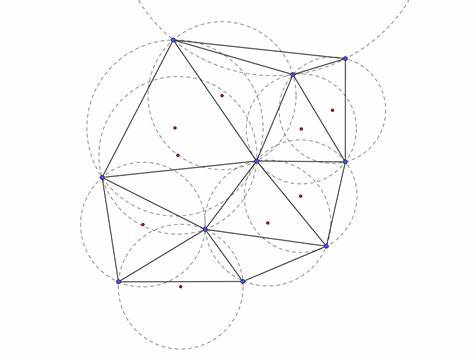
Die Delaunay-Triangulation gehört zu den grundlegenden Methoden der Computational Geometry und spielt eine zentrale Rolle bei der Verarbeitung von Punktemengen in der Ebene. Sie erzeugt ein Dreiecksnetz, das bestimmte optimale Eigenschaften besitzt und in zahlreichen Anwendungen wie Geoinformationssystemen (GIS), Computergrafik, Finite-Elemente-Methoden oder sogar der Netzwerkmodellierung eingesetzt wird. Die effiziente Umsetzung der Delaunay-Triangulation ist maßgeblich für die Performance komplexer Analysen und Simulationen. Grundsätzlich basiert die Delaunay-Triangulation auf dem Ziel, aus einer Menge diskreter Punkte ein Dreiecksnetz zu erstellen, so dass kein Punkt innerhalb des Umkreises eines Dreiecks liegt. Dieses charakteristische Kriterium führt dazu, dass die Dreiecke möglichst „rund“ wirken und scharfe Winkel minimiert werden, was gerade bei der Flächenerfassung und der Netzgenerierung von großer Bedeutung ist.
Der Netzaufbau ermöglicht es, Verbindungen möglichst optimal zu gestalten, da Dreiecke immer eine gemeinsame Kante miteinander teilen und somit eine übersichtliche geometrische Struktur entsteht. Der Algorithmus greift häufig auf bewährte Konzepte wie die Bowyer-Watson-Methode zurück. Diese Vorgehensweise ergänzt schrittweise Punkte, indem sie bestehende Dreiecke aufsprengt und neu verteilt, um die Delaunay-Bedingungen zu erfüllen. Dabei werden zunächst alle Punkte in der Ebene sortiert, oftmals mithilfe der Hilbert-Sortierung. Diese Form der Sortierung ordnet Punkte entlang einer Hilbert-Kurve, einer kontinuierlichen Raumfüllenden Kurve, die die lokale Nähe von Punkten untereinander bewahrt und somit die Effizienz der Triangulation erheblich steigert.
Insbesondere bei großen Punktmengen bietet die Hilbert-Sortierung eine Möglichkeit, den Algorithmus schneller und speichereffizienter zu gestalten. Im Gegensatz zu anderen Triangulationsformen ist die Delaunay-Triangulation besonders stabil gegenüber Punktbewegungen. Werden Punkte minimal verschoben, passt sich das Dreiecksnetz dynamisch an, was vor allem bei Animationen oder Echtzeitauswertungen von Bedeutung ist. Außerdem lassen sich aus dem erzeugten Dreiecksnetz weitere Strukturen ableiten, die wichtige Eingaben für komplexe Anwendungen darstellen. So ist es beispielsweise möglich, mithilfe der Delaunay-Dreiecke minimale Spannbäume (Minimum Spanning Trees) zu erstellen, die im Bereich der Netzwerktopologien oder in der Graphentheorie vielfach gebraucht werden.
Aus der praktischen Sicht bietet eine Softwarebibliothek für Delaunay-Triangulation idealerweise verschiedene Klassen, die sowohl die reine Berechnung als auch die Visualisierung der Triangulation abdecken. Während eine Hauptklasse lediglich die Koordinaten der Punkte entgegennimmt und die Dreiecksverbindungen berechnet, kann eine weitere Klasse auf die Darstellung des resultierenden Graphen eingehen. Dies erleichtert nicht nur die Analyse, sondern auch die Fehlerkontrolle oder die Präsentation der erzeugten Daten. Die Implementierung des Algorithmus erlaubt es, auch bei Millionen von Punkten relativ schnell eine Delaunay-Triangulation zu erzeugen. Die Kombination von Hilbert-Sortierung und Bowyer-Watson-Algorithmus ist dabei der Schlüssel für die hohe Geschwindigkeit.
Die Hilbert-Sortierung bewirkt, dass beim Einfügen neuer Punkte in die Triangulation die Umkreise der Dreiecke lokal untersucht werden können. Dadurch sind aufwendige globale Suchvorgänge nicht notwendig, was zu einer signifikanten Reduzierung der Laufzeit führt. Der praktische Nutzen der Delaunay-Triangulation zeigt sich vor allem in der Modellierung von Oberflächen und Geländedaten. In der Geografie werden Koordinaten von Geländemessungen trianguliert, um Höhenprofile zu errechnen und Karten zu erstellen. Auch in der Physik oder im Maschinenbau dient die Delaunay-Triangulation als Grundlage für das Erstellen geeigneter Rechenmodelle.
Die Vernetzung ermöglicht es, komplexe Strukturen auf einfache geometrische Formen zu reduzieren, die anschliessend numerisch simuliert werden können. So entsteht ein effizientes Werkzeug zur Berechnung von Belastungen, Strömungen oder Wärmediffusion. Darüber hinaus findet die Delaunay-Triangulation Anwendung im Bereich der Computergrafik, etwa bei der Erzeugung von Meshes für 3D-Modelle. Die gleichmässige Verteilung der Punkte und die minimierten Winkel sorgen dafür, dass Visualisierungen präzise und realistisch dargestellt werden. Viele moderne Grafik-Engines nutzen Delaunay-Triangulationen, um Oberflächen meshen zu können, die sich dynamisch ändern – beispielsweise durch Benutzerinteraktion oder bei Animationen.
Auch in der Netzwerkoptimierung spielt die Delaunay-Triangulation eine Rolle. Beachten lässt sich dabei, dass die erstellten Dreiecksverbindungen eine gute Basis zur Bestimmung kürzester Verbindungen oder minimaler Spannbäume bieten. Dies ist für das Design von Kommunikationsnetzwerken, Distribution oder elektrischen Netzen bedeutsam, da so Ressourcen optimal verteilt und verwendet werden können. Die Geometrie der Triangulation gewährleistet in solchen Anwendungen eine effiziente und robuste Lösung. Die Algorithmus-kritische Komponente bleibt die korrekte Behandlung von Randpunkten und Spezialfällen wie kollinearen Punkten oder identischen Koordinaten.
Moderne Implementierungen integrieren daher zahlreiche Optimierungen und Fehlererkennungsmechanismen, die sowohl die Stabilität als auch die Qualität der Triangulation garantieren. Solche Maßnahmen sind essenziell, um in professionellen Anwendungen verlässliche Ergebnisse zu erhalten. Zukunftsweisend lässt sich festhalten, dass die Weiterentwicklung von Delaunay-Triangulationen eng mit der Verbesserung von Hardware-Ressourcen und paralleler Verarbeitung verknüpft ist. Multi-Core-Prozessoren und GPU-Beschleunigung bieten spannende Möglichkeiten, die Geschwindigkeit und Größe der zu verarbeitenden Punktmengen weiter zu erhöhen. Besonders bei hochauflösenden Analysen und real-time Anwendungen wird dieser Trend zunehmend an Bedeutung gewinnen.
Zusammenfassend lässt sich sagen, dass die Delaunay-Triangulation ein leistungsfähiges und vielseitiges Werkzeug der räumlichen Datenverarbeitung ist. Sie kombiniert mathematische Eleganz mit pragmatischem Nutzen und eröffnet zahlreiche Chancen in Wissenschaft, Technik und Industrie. Durch moderne Optimierungen wie Hilbert-Sortierung und den Bowyer-Watson-Algorithmus gelingt es, auch große und komplexe Punktmengen effizient zu triangulieren. Die daraus resultierenden Dreiecksnetze liefern eine solide Basis für Berechnungen, Visualisierungen und Netzwerkanalysen aller Art und sind aus der heutigen computergestützten Geometrieverarbeitung nicht mehr wegzudenken.