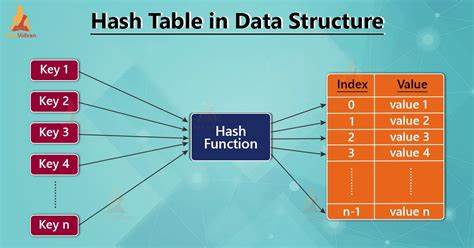
In der Welt der Programmierung sind Datenstrukturen das Fundament effizienter Algorithmen und Anwendungen. Eine der wichtigsten Datenstrukturen, die in nahezu allen Programmiersprachen verwendet wird, ist die Hash-Tabelle. Sie ermöglicht schnelle Zugriffe auf Daten durch die Verknüpfung von Schlüsseln mit Werten. Dennoch sind klassische Hash-Tabellen oft mutierbar, was bedeutet, dass sie Veränderungen direkt am bestehenden Speicher vornehmen. Dies bringt Probleme mit sich, insbesondere wenn es um Parallelverarbeitung oder funktionale Programmierparadigmen geht.
Die Antwort auf diese Herausforderungen sind funktionale Hash-Tabellen, insbesondere basierend auf einer cleveren Datenstruktur namens Hash Array Mapped Trie, kurz HAMT. Funktionale Programmierung setzt auf Unveränderlichkeit von Datenstrukturen. Dies führt zur Idee der Persistenz, bei der jede Datenstrukturänderung eine neue Version anlegt, die die alte Version nicht zerstört, sondern gemeinsam mit ihr existiert. Listen sind hier ein typisches Beispiel: Sie sind einfach zu erweitern, teilen sich aber ihre alten Elemente. Allerdings ist die Suche in Listen linear, was bei großen Datenmengen ineffizient ist.
Hash-Tabellen sind hier weit überlegen, da sie im Durchschnitt Zugriffe in konstanter Zeit ermöglichen, doch ihre typische Umsetzung als mutable Datenstruktur widerspricht der funktionalen Philosophie. Ein Ansatz, um diese Einschränkungen zu überwinden, ist die Nutzung von HAMTs. Entwickelt von Phil Bagwell, bieten diese eine effiziente, ineffektive persistente Implementierung von Hash-Tabellen. HAMTs kombinieren die Idee von tries – spezieller Baumstrukturen, die Schlüssel anhand ihrer Präfixe speichern – mit einem hohen Verzweigungsgrad. Dabei ist der Baum im Vergleich zu binären Bäumen breit und flach, typischerweise mit einer Verzweigung von 32.
Dadurch wird die Höhe des Baums stark reduziert und die Zeitkomplexität für Einfügungen, Löschungen und Abfragen liegt bei praktisch konstanter Zeit. Im Gegensatz zu klassischen Bäumen speichern HAMTs die Schlüssel nicht in allen Knoten, sondern ausschließlich in den Blättern. Die Verzweigung bestimmt jeden Schritt auf dem Pfad von der Wurzel zu einem Blatt, wobei jeweils bestimmte Bits des Hashwerts eines Schlüssels ausgewertet werden. Der Hashwert eines Schlüssels wird hierzu in Segmente zerlegt, die als Indizes in eine Array-ähnliche Struktur dienen. Das Besondere daran ist die Verwendung von Bitmap-Arrays, die den Speicher effizient halten und sparsamen Umgang selbst bei spärlicher Belegung gewährleisten.
Eine wichtige Eigenschaft von HAMTs ist ihre Speicher- und Leistungsoptimierung durch eine sogenannte Sparse-Array-Darstellung. Anstatt für jeden Knoten ein vollständiges Array mit 32 Positionen vorzuhalten, wird nur ein kompakter Speicher reserviert, der ausschließlich belegte Einträge enthält. Ein Bitmap hält dabei fest, welche der 32 Positionen aktuell verwendet werden. Durch das Zählen der gesetzten Bits vor einer bestimmten Position lässt sich schnell der tatsächliche Index im kompakten Array bestimmen. Diese Technik minimiert den Speicherverbrauch signifikant und verbessert die Cache-Effizienz.
Die Einfügeoperation verläuft rekursiv und beginnt an der Wurzel des HAMT. Zunächst wird der Hashwert des neuen Schlüssels berechnet. Die höchsten 5 Bits werden genutzt, um die nächste Verzweigung zu bestimmen. Ist der Platz noch frei, wird der Schlüssel dort als Blatt abgelegt. Besteht jedoch bereits ein Konflikt, also wenn ein anderer Schlüssel an dieser Position liegt, entsteht ein neuer Unterbaum.
Dabei werden die nächsten Bits des Hashs betrachtet, um die beiden Schlüssel zu differenzieren. Dieser Prozess kann sich rekursiv wiederholen, bis der Konflikt gelöst ist. Im schlimmsten Fall, wenn die Hashwerte zweier Schlüssel komplett identisch sind, wird auf eine einfache Listenstruktur zur Auflösung der Kollision zurückgegriffen. Diese rekursive Einfügeweise sorgt dafür, dass nur die betroffenen Knoten auf dem Pfad zu einem Schlüssel neu erstellt werden. Alle anderen Knoten werden unverändert übernommen und somit geteilt.
Das Ergebnis ist eine persistente Datenstruktur, die dank dieser Teilbarkeit äußerst speichereffizient neue Versionen nach Änderungen bereitstellt. Die Suche nach einem Schlüssel in einem HAMT ist ähnlich elegant. Der Hashwert des Schlüssels wird berechnet und Schritt für Schritt anhand von Teilbits ausgewertet. An jeder Ebene wird anhand der Bitmap geprüft, ob sich ein Eintrag an der gewünschten Position befindet. Falls nein, ist der Schlüssel nicht vorhanden, und die Suche endet.
Ist ein Stapel vorhanden, wird die Suche im entsprechenden Unterbaum fortgesetzt. Andernfalls wird der Wert zurückgegeben, wenn der Schlüssel passt, oder die Suche abgebrochen. Auch das Löschen eines Schlüssels aus einem HAMT verläuft nach dem gleichen Muster – die Änderung wird rekursiv durchgeführt, indem nur betroffene Knoten neu aufgebaut werden. Ein besonderes Augenmerk liegt bei der Speicheroptimierung durch Pfadkompression: Wenn nach dem Löschen ein Unterbaum nur noch einen Eintrag besitzt, wird dieser Unterbaum eliminiert und durch den einzelnen Eintrag ersetzt, um unnötige Tiefen zu vermeiden. HAMTs sind mittlerweile in funktionalen Programmiersprachen wie Clojure fest integriert und gelten dort als das Standardfundament für effiziente assoziative Datenstrukturen.
Ursprünglich in der Forschung von Phil Bagwell vorgestellt, finden sie zunehmend Verwendung in modernen Anwendungen, bei denen Unveränderlichkeit, Effizienz und Parallelisierbarkeit entscheidend sind. Ein herausragendes Beispiel für ihre Anwendung ist das Lisp-Derivat Guile. Obwohl Guile traditionell mutable Hash-Tabellen bereitstellt, wird dort aktuell ein alternativer Ansatz mit VLists genutzt, eine weitere Datenstruktur von Bagwell. Es zeigt sich aber, dass HAMTs besser geeignet sind, um die Anforderungen funktionaler Programmierung zu erfüllen, insbesondere in Bereichen, die hohe Performance und Speicheroptimierung erfordern. Die Vorteile der funktionalen Hash-Tabellen auf Basis von HAMTs sind vielfältig.
Neben der Unveränderlichkeit unterstützen sie native Persistenz, was unvergleichlich bessere Sicherheit und Vorhersagbarkeit von Programmen gewährleistet. Dies erleichtert das Arbeiten in nebenläufigen und mehrkernigen Umgebungen, da Datenstrukturen ohne Synchronisationsprobleme geteilt werden können. Zudem sind HAMTs hervorragend geeignet, um schrittweise Änderungen historisch nachzuvollziehen oder Zustände zu speichern. Trotz der beeindruckenden Technik sind HAMTs nicht frei von Komplexität. Die Implementierung erfordert ein gutes Verständnis von Bitmanipulationen, effizienten Speicherzugriffen und rekursiven Algorithmen.
Besonders die Verwaltung von Kollisionen bei identischen Hashcodes sowie das Pfadkompressionsverfahren bei Löschungen sind anspruchsvolle Themen. Dennoch ermöglichen sie eine beachtliche Performance, die mutablen Hash-Tabellen in nichts nachsteht, dabei aber die Sicherheit und Vorteile funktionaler Programmierung bewahrt. Die Zukunft der Datenverarbeitung im funktionalen Paradigma wird maßgeblich durch innovative Strukturen wie HAMTs geprägt sein. Durch ihre Kombination aus Effizienz, Persistenz und Immutability bieten sie Programmierern eine robuste Grundlage für die Entwicklung moderner Software, die in Zeiten von Multi-Core-Prozessoren und parallelen Anwendungen unverzichtbar ist. Die aktuelle Forschung und Entwicklung im Umfeld von Scheme und Guile nimmt HAMTs als eine Schlüsseltechnologie wahr.





![Faulty 120W charger analysis (Anker GAN Prime) [video]](/images/16EF8747-791A-4814-8817-21E4FFA25C9F)
