Die Suche nach dem kürzesten Weg in Graphen ist ein zentraler Bestandteil vieler Computeranwendungen, von der Netzwerkanalyse über soziale Netzwerke bis hin zur Routenplanung. Breitensuche (BFS) ist eine vertraute und bewährte Methode, um diese Aufgabe in ungewichteten Graphen zu lösen. Das Konzept der bidirektionalen Breitensuche (Bidirectional BFS) baut darauf auf, indem es die Suche gleichzeitig von Start- und Zielknoten ausführt und verspricht, die Effizienz drastisch zu verbessern. Doch überraschenderweise sind viele Implementierungen dieses vermeintlich einfachen Algorithmus fehlerhaft und liefern falsche Ergebnisse. Die Ursache für diese Ungenauigkeiten ist auf subtile konzeptionelle Missverständnisse zurückzuführen, die selbst in renommierten Quellen verbreitet sind.
Die folgende Analyse beleuchtet diese Fehlerquellen, erklärt die korrekte Funktionsweise der bidirektionalen Breitensuche und zeigt praktische Optimierungen auf, um zuverlässige und schnelle Pfadsuchen zu ermöglichen. Ein tieferes Verständnis dieser Thematik ist essenziell, um die Vorteile der bidirektionalen Suche voll auszuschöpfen und Fehlersituationen zu vermeiden. Grundlagen von Graphen und Pfadsuche Um die Problematik rund um die bidirektionale Breitensuche zu verstehen, ist es wichtig, zunächst die Grundlagen von Graphen und der Pfadsuche zu erläutern. Ein Graph besteht aus Knoten (Vertices) und Kanten (Edges), die diese Knoten miteinander verbinden. Je nach Anwendung können Kanten gerichtet oder ungerichtet sein, und sie können Gewichte tragen oder ungewichtet sein.
Für die klassische Breitensuche im Kontext dieses Artikels betrachten wir meist ungerichtete und ungewichtete Graphen. Die Aufgabe besteht darin, einen möglichst kurzen Weg zwischen zwei Knoten zu finden. Die Breitensuche (BFS) funktioniert, indem sie die Nachbarn eines Startknotens systematisch erkundet – zuerst die Knoten direkt am Start, dann deren Nachbarn, und so weiter, Schicht für Schicht. Dieses Vorgehen garantiert, dass der erste Weg, der zum Ziel gelangt, der kürzeste ist, denn Knoten auf niedrigeren Ebenen entsprechen kürzeren Wegen. Warum die bidirektionale Breitensuche? BFS ist schlicht und effektiv, aber an großen Graphen stößt sie schnell hinsichtlich Zeit und Ressourcen an Grenzen.
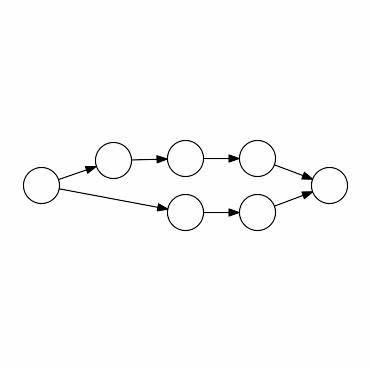
Gerade bei weit auseinanderliegenden Knoten wächst der Suchraum exponentiell mit der Distanz. Hier setzt die bidirektionale BFS an: Anstatt nur vom Startknoten aus zu suchen, wird die Suche gleichzeitig vom Start- und dem Zielknoten ausgeführt. Diese beiden Suchfronten treffen sich idealerweise irgendwo in der Mitte, wodurch die Anzahl der zu suchenden Knoten exponentiell reduziert werden kann. Das Prinzip klingt naheliegend – wenn die Distanz zwischen zwei Knoten D ist und der durchschnittliche Verzweigungsfaktor b, so visitieren einfache BFS etwa b hoch D Knoten, während zwei parallele BFS je b hoch D geteilt durch 2 Knoten durchsuchen, insgesamt also deutlich weniger. Daraus ergibt sich eine Zeitersparnis, die insbesondere bei sehr großen Graphen mit hoher Verzweigung zum Tragen kommt.
Der fundamentale Fehler vieler Implementierungen Trotz der eleganten Idee stellt sich in der Praxis ein abweichendes Verhalten ein: Viele Implementierungen der bidirektionalen BFS liefern nicht immer den kürzesten Weg. Der Grund liegt in einem entscheidenden Detail – dem Fortschreiten der Suchfronten. Während eine klassische BFS Ebene für Ebene durchläuft und erst dann zur nächsten Ebene übergeht, verhalten sich viele bidirektionale Suchalgorithmen inkorrekt, indem sie Knoten jeweils einzeln verarbeiten und sofort stoppen, sobald sich Suchfronten treffen. Dieses Vorgehen führt dazu, dass die Algorithmus instabil wird – er kann einen Pfad liefern, der zwar gültig, aber nicht minimal ist. Die Ursache ist, dass das gleichzeitige Abtasten beider Fronten nicht streng schichtweise erfolgt.
Da eine Seite schneller oder in einer anderen Reihenfolge Knoten behandelt als die andere, kann der Algorithmus an einer Stelle stoppen, die keinen optimalen Schnittpunkt zwischen Start- und Zielsuche darstellt. Die richtige Interpretation: Level-für-Level-Erweiterung Das Schlüsselelement für eine richtige bidirektionale BFS ist, dass beide Suchfronten strikt synchron auf Levelbasis voranschreiten und nicht bei jedem Besuch eines einzelnen Knotens stoppen. Jeweils alle Knoten der aktuellen Tiefe beziehungsweise Ebene müssen umfassend durchgesehen werden, bevor die Suche zur nächsten Tiefe übergeht und mit der anderen Suchseite verglichen wird. Dies garantiert, dass die Knoten, die sich treffen, tatsächlich auf minimalem Abstand von Start beziehungsweise Ziel liegen, und somit der kürzeste Pfad vorliegt. Diese strikte Ebenensynchronisierung ist in der Praxis allerdings komplizierter zu implementieren als auf den ersten Blick erkennbar.
Viele öffentliche Implementierungen und Tutorials vereinen die Suchfronten nicht konsequent auf diesem Level, was zu falschen Pfaden führt. Praktische Auswirkungen und Beispiele Auf großen Datenmengen, etwa in sozialen Netzwerken oder Straßennetzen, kann eine falsche bidirektionale BFS fehlerhafte Routen ausgeben, die etwa eine Station oder einen Knoten zu viel enthalten. Solche Fehler sind schwer erkennbar, weil der Unterschied oft klein und nicht offensichtlich ist. Doch in Echtzeitanwendungen oder bei automatischer Entscheidungsfindung sind sie fatal. Beispiele für solche Fehlerhafte Implementierungen finden sich auf zahlreichen bekannten Plattformen und Code-Repositories.
Viele sind nicht nur falsch, sondern kopieren den Fehler von vorgängigen Seiten, was sich zur Regel macht. Ein prominentes Beispiel ist die populäre Seite GeeksforGeeks, deren Codebasis zu diesem Thema seit Jahren unzureichend ist und von vielen Projekten unkritisch übernommen wird. Sogar einige KI-gestützte Tools, die Code generieren, reproduzieren diesen Fehler. Lösungen und Optimierungen Um die Effizienz und Korrektheit der bidirektionalen BFS zu verbessern, gibt es neben dem korrekten Level-für-Level-Vorgehen eine weitere Verbesserung: die dynamische Auswahl der Suchseite, die als nächstes erweitert wird. Statt strikt abwechselnd jeweils eine Ebene voranzuschreiten, wird die Front bevorzugt, die gerade weniger Knoten in der Warteschlange enthält.
Das reduziert deutlich die Anzahl der zu prüfenden Knoten und beschleunigt den Suchprozess. Eine weitere praktische Empfehlung ist die sorgfältige Überprüfung der Schnittstellen, an denen die zwei Suchfronten zusammentreffen, sowie eine saubere Verwaltung der besuchten Knoten, um Überschneidungen akkurat zu detektieren und rekonstruieren zu können. Dies verhindert, dass ein vorzeitiges Stoppen aufgrund einer unvollständigen Erkundung erfolgt. Bedeutung für die Praxis und zukünftige Forschung Die Tatsache, dass selbst heute viele gängige Quellen fehlerhafte bidirektionale BFS-Codebeispiele verbreiten, zeigt, wie subtil algorithmische Details in der Praxis sein können und welche Bedeutung eine fundierte Implementierungsprüfung hat. Für Entwickler in den Bereichen Datenanalyse, Netzwerktechnik und Routenplanung ist es entscheidend, diese Erkenntnisse zu kennen.
Zugleich eröffnet die korrekte bidirektionale BFS Perspektiven, um Pfadsuchen in riesigen Graphen mit Millionen von Knoten performant zu gestalten. Gerade in Zeiten von Big Data und immer komplexeren Netzwerkstrukturen zählt jede Optimierungsschleife. Die Kombination aus striktem Ebenenprinzip und dynamischem Seitenwechsel am Suchvordergrund gewährleistet einerseits Korrektheit und andererseits eine signifikante Beschleunigung. Fazit Bidirektionale Breitensuche ist ein mächtiges Werkzeug, das gegenüber der klassischen Breitensuche großzügige Zeiteinsparungen verspricht. Dennoch ist ihre korrekte Anwendung nicht trivial.
Das weit verbreitete Missverständnis besteht darin, die beiden Suchfronten nicht synchron Level-für-Level voranschreiten zu lassen. Dadurch entstehen bei vielen Implementierungen falsche Pfadergebnisse. Eine korrekte Implementierung erfordert, dass beide Suchen gemeinsam jeweils alle Knoten einer Ebene vollständig besuchen und alle Knoten dieser Ebene abgearbeitet sein müssen, bevor mit der nächsten Ebene weitergemacht wird. Zusätzlich bewährt sich als Optimierung die Priorisierung der Seite mit weniger ausstehenden Knoten. Für alle, die effiziente Pfadsuchen auf großen ungewichteten Graphen realisieren möchten, ist es unabdingbar, diese Algorithmusanalyse zu kennen und umzusetzen – denn nur so lassen sich Korrektheit, Geschwindigkeit und Robustheit in Einklang bringen.
Wer sich darauf verlässt, Code aus vermeintlich vertrauenswürdigen Quellen ohne eigene Prüfung zu übernehmen, riskiert, ineffiziente oder gar falsche Ergebnisse zu erzielen. Die besondere Herausforderung der bidirektionalen BFS erinnert daran, dass fundamentale Algorithmen trotz ihres hohen Alters und scheinbarer Einfachheit eine präzise Umsetzung erfordern, um ihre theoretischen Vorteile im praktischen Einsatz zu entfalten. Insofern ist es ratsam, Algorithmen tiefgreifend zu verstehen, kritisch zu hinterfragen und den eigenen Code stets sorgfältig zu verifizieren.