Was Mücken mich über Algorithmendesign lehrten: Erkenntnisse aus der Biologie für die Informatik

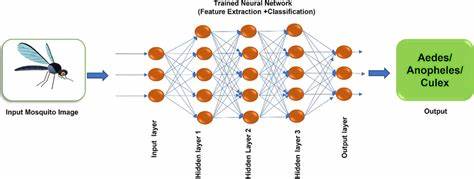
Im Alltag begegnen wir Mücken meist nur als lästige Stechinsekten, die uns in lauen Sommernächten den Schlaf rauben. Doch was, wenn uns diese kleinen Kreaturen auch wertvolle Lektionen über die Welt der Algorithmen und Datenstrukturen lehren könnten? Genau das entdeckte Kok Rui Wong während seiner Zeit in der singapurischen Armee, als er statt der üblichen Waffen- und Kampftrainings der Aufgabe zugeteilt wurde, Mücken zu identifizieren – eine scheinbar ungewöhnliche aber hochinteressante Tätigkeit, in der sich Biologie und Informatik auf faszinierende Weise überschneiden. Die Grundlage für die Mückenidentifikation bildet ein sogenannter dichotomer Schlüssel. Dabei handelt es sich um eine Reihe von ja/nein-Fragen, die wie ein binärer Entscheidungsbaum aufgebaut sind. Jede Frage führt je nach Antwort zu einer Verzweigung, bis am Ende eine eindeutige Bestimmung der Mückenart steht.

Dieses Vorgehen weist eine klare Parallele zu Algorithmendesign auf: Der dichotome Schlüssel bildet einen Suchbaum ab, dessen Traversierung im schlimmsten Fall die gesamte Länge des Baums durchlaufen muss – also eine lineare Zeitkomplexität O(N) besitzt. Doch hier beginnt die spannende Entdeckung. Mit den rudimentären Informatikkenntnissen aus der Schulzeit kam Wong auf die Idee, dass man den Baum balancieren könnte. Ein balancierter Baum würde bedeuten, dass die Suche im Durchschnitt nach O(log N) Schritten zum Ziel führt – ein signifikanter Geschwindigkeitsvorteil. Anstatt des klassischen dichotomen Schlüssels baute er einen sogenannten polyclaven Schlüssel, der nicht nur zwei, sondern gleich mehrere Antwortmöglichkeiten bei jedem Schritt zuließ.

Dies wiederum erlaubte es, die Anzahl der in jedem Schritt auszuschließenden Arten deutlich zu erhöhen. Dieser Ansatz klingt auf dem Papier überzeugend und wurde mit entsprechenden Zeitmessungen überprüft. Überraschenderweise zeigte sich jedoch, dass der polyclave Schlüssel in der praktischen Anwendung sogar langsamer als der traditionelle dichotome Schlüssel war. Warum? Die Antwort liegt in den Details der tatsächlichen Anwendung und der Verteilung der Eingabedaten – eine Erkenntnis, die in der Informatik häufig unterschätzt wird. Die Mückenarten, die in der Praxis am häufigsten vorkommen, werden im klassischen dichotomen Schlüssel sehr früh erkannt.

Diese sogenannten häufigen Fälle erfordern nur wenige Entscheidungsschritte. Der Worst-Case, also die längste Suchdauer für seltenere Arten, ist in der Realität nur selten relevant. Diese Erkenntnis erinnert an das Prinzip, Algorithmen nicht nur anhand von Worst-Case-Szenarien zu bewerten, sondern auch ihren Durchschnitt oder ihre praktische Ausführungshäufigkeit in typischen Situationen zu berücksichtigen. Ein Beispiel aus der Informatik hierfür sind Hashtabellen, bei denen ein Großteil der Zugriffe fast konstant schnell erfolgt, während Kollisionen und Suchzeiten im Worst-Case deutlich steigen können, diese aber selten eintreten. Ähnlich wie bei Mücken ist ein System, das im Durchschnitt schnell arbeitet und gelegentlich langsamer ist, oftmals praktikabler als eines, das im Worst-Case schneller wäre, aber im Durchschnitt langsamer operiert.

Ein weiterer, oft unbeachteter Faktor ist die tatsächliche Dauer der einzelnen Entscheidungsschritte. In der asymptotischen Analyse werden alle Operationen oft als gleichwertig behandelt, doch die Realität sieht anders aus. Einige Untersuchungsschritte, wie das Überprüfen einer auffälligen morphologischen Eigenschaft, sind mit einem Blick erledigt. Andere erfordern minutiöses Einstellen des Mikroskops, Lichtanpassungen und vorsichtige Manipulation des fragilen Insekts am Präparat – ein enormer Aufwand, der Zeit und Konzentration kostet. Diese Heterogenität zeigt auf, dass das reine Zählen von Prüfungen oder algorithmischen Schritten keine exakte Aussage über die tatsächliche Laufzeit erlaubt.

Die Kosten eines Schritts hängen stark von dessen Komplexität ab. In der Welt der Algorithmen bedeutet dies, neben der theoretischen Zeitabschätzung auch die praktischen, hardware- und anwendungsabhängigen Kosten eines Befehls berücksichtigen zu müssen. Hinzu kommt, dass der Umfang der Artendaten begrenzt ist. Mit etwa 48 möglichen Gattungen und einigen hundert Arten war die Datenbasis überschaubar. Für kleine Datenmengen spielen asymptotische Vorteile einer Algorithmusverbesserung oft nur eine untergeordnete Rolle.

Ein linear durchsuchter Baum mit wenigen Dutzend Einträgen performt in vielen Fällen ausreichend schnell und ist oft sogar effizienter als strikt optimierte Strukturen, da diese Konstanten und Overheads aufweisen, die sich in kleinen Größenordnungen negativ bemerkbar machen. Im Studium wird man später lernen, dass Big-O-Notation und asymptotische Betrachtungen erst ab einem gewissen Punkt, dem sogenannten Crossover-Punkt, relevanter werden. Unterhalb dieses Punktes dominieren konstante Faktoren, Overhead und praktische Detailunterschiede. Diese praktischen Erfahrungen aus einer ganz anderen Domäne liefern damit wichtige Einblicke für angehende Entwickler und Algorithmendesigner. Die Lehren aus der Mückenbestimmung gehen zudem darüber hinaus in philosophische Richtungen der Softwareentwicklung.

Man sollte beim Optimieren von Algorithmen immer den Anwendungskontext im Blick behalten – eine theoretisch bessere Lösung kann in der Praxis schlechter abschneiden, wenn wichtige Details ausblenden werden. Speziell beim Umgang mit Realdaten, die oft unregelmäßig verteilt und mit Messfehlern behaftet sind, sind pragmatische Lösungen mit Blick auf Benutzererfahrung und Aufwand häufig vorteilhafter als starre theoretische Maximen. Die Mücken identifizieren zu lernen, half Wong schließlich auch, Erfahrungswerte zu sammeln, die bei der späteren Arbeit mit Informatikproblemen hilfreich waren. Die gedankliche Verbindung zwischen der klassischen Biologie und moderner Algorithmustechnik bewies, dass interdisziplinäres Denken die Kreativität fördern und unkonventionelle Lösungsansätze ermöglichen kann. Neben der verbesserungswürdigen Unsicherheit bei der Identifikation, insbesondere bei seltenen Arten, zeigte sich auch die Bedeutung der Datenstrukturenauswahl für verschiedene Problemgrößen.

Kleine Probleme profitieren oft von einfachen linearen Strukturen. Große Probleme erfordern komplexere, balancierte Strukturen und Heuristiken. Beides zu verstehen ist entscheidend, um optimale Software zu entwickeln. Zusammenfassend erlaubt der Einblick in die einfachen Insekten und ihre morphologische Klassifikation einen Blick auf fundamentale Prinzipien der Informatik: die Relevanz der Datenverteilung, die Unterschiedlichkeit der Operationen in ihrer tatsächlichen Laufzeit und die Grenzen der asymptotischen Analyse in praktischen Anwendungen. Auch lässt sich erkennen, dass der Weg von der Theorie zur Praxis nicht immer geradlinig ist und dass man häufig einen Kompromiss zwischen Eleganz und Benutzbarkeit finden muss.

Die Geschichte zeigt, dass komplexe Algorithmen nicht immer die effizientesten oder nützlichsten sind, wenn man praktische Anwendungsfälle betrachtet. Wir sollten daher stets offen sein für unkonventionelle Ansätze und die Absicht hinter einem System genau verstehen, bevor wir Optimierungen vornehmen. Die Welt der Mücken hat damit unerwartet viel zur Entwicklung von reflexivem und praxisbezogenem Algorithmusdenken beigetragen – eine Lektion, die weit über Biologie und Informatik hinausgeht.