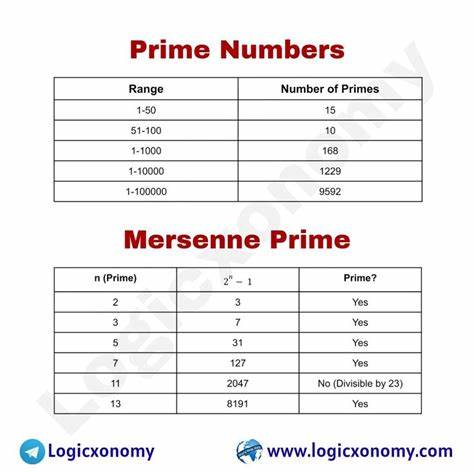
Mersenne-Primzahlen sind seit Jahrhunderten ein zentrales Thema in der Zahlentheorie und faszinieren Mathematiker durch ihre besondere Form und ihre einzigartigen Eigenschaften. Sie sind definiert als Primzahlen, die sich als 2^p - 1 darstellen lassen, wobei p selbst eine Primzahl ist. Diese spezifische Form macht sie zu einem spannenden Untersuchungsgegenstand, nicht nur innerhalb der reinen Mathematik, sondern auch im Bereich der Informatik und Kryptografie. Doch trotz ihrer klaren Definition gibt es eine interessante Gruppe von Zahlen, die äußerlich den Mersenne-Primzahlen sehr ähnlich sehen, jedoch keine Primzahlen sind. Diese sogenannten zusammengesetzten Zahlen, die wie Mersenne-Primzahlen aussehen, werfen faszinierende Fragen auf und fordern das Verständnis der Zahlentheorie heraus.
Zusammengesetzte Zahlen ähnlicher Gestalt entstehen, wenn man gleiche binäre Formen betrachtet, die jedoch durch andere Faktoren teilbar sind. Während echte Mersenne-Primzahlen nur zwei Teiler besitzen – die 1 und sich selbst – besitzen diese zusammengesetzten Gegenstücke mehr als zwei Teiler, was sie in der Kategorien „Primzahl“ ausschließt. Die Herausforderung liegt oft darin, diese zusammengesetzten Zahlen von echten Mersenne-Primzahlen zu unterscheiden, da die äußeren Merkmale wie Länge, Form und binäre Struktur eine starke Täuschung bieten. Die theoretische Bedeutung solcher Zahlen ist hoch. Zum einen ermöglichen sie ein tieferes Verständnis über die Struktur der Primzahlen und deren Verteilung.
Zum anderen zeigt die Untersuchung dieser zusammengesetzten Zahlen, wie komplex die Primzahlsuche wirklich ist und warum einfache Muster für sich genommen nicht ausreichend sind, um Primzahlen zuverlässig zu identifizieren. Mersenne-Primzahlen werden häufig zur Konstruktion großer Primzahlen verwendet, insbesondere in Projekten wie GIMPS (Great Internet Mersenne Prime Search), das sich der Suche nach immer größeren Mersenne-Primzahlen widmet. Die Tatsache, dass es zusammengesetzte Zahlen gibt, die diesen Mersenne-Zahlen zum Verwechseln ähnlich sehen, bedeutet, dass stetige Prüfung und Verifikation unverzichtbar sind. Moderne Algorithmen zur Primzahlprüfung müssen daher besonders robust sein, um diese falschen Kandidaten auszuschließen. Dies hat zudem Auswirkungen auf die Kryptografie.
Da viele Verschlüsselungsverfahren von der Schwierigkeit großer Primzahlen profitieren, kann das versehentliche Einbeziehen solcher zusammengesetzten Zahlen die Sicherheit beeinträchtigen. Deshalb ist es unerlässlich, Primzahlen mit höchster Präzision zu identifizieren, insbesondere wenn sie bei der Verschlüsselung sensibler Daten verwendet werden. Die Geschichte der Untersuchung komposit der Mersenne-ähnlichen Zahlen ist lang und voller Überraschungen. Zahlreiche mathematische Entdeckungen entstanden durch die Suche nach Ausnahmefällen oder Gegenbeispielen, die Ursprüngliche Theorien infrage stellten oder erweiterten. Dass zusammengesetzte Zahlen trotz ihrer Ähnlichkeit zu Mersenne-Primzahlen existieren, veranschaulicht wie reichhaltig und tiefgründig das Feld der Zahlentheorie ist.
Von einem praktischen Blickwinkel aus betrachtet, unterstützen Forschungen in diesem Bereich auch die Weiterentwicklung von Rechenmethoden und Softwarelösungen, die in Wissenschaft und Technik weit verbreitet sind. Ganz gleich ob es um Simulationen, Kryptografie oder Datenkompression geht, wissen wir heute, dass das Verständnis dieser scheinbar einfachen Strukturen weitreichende Konsequenzen hat. Abschließend lässt sich festhalten, dass zusammengesetzte Zahlen, die wie Mersenne-Primzahlen aussehen, mehr als nur eine mathematische Kuriosität sind. Sie symbolisieren die Tiefe, Komplexität und Schönheit der Mathematik; zeigen die Grenzen unseres Wissens auf und motivieren zu neuen Forschungen. Für jeden, der sich mit Zahlen, Algorithmen oder der Sicherheit digitaler Systeme beschäftigt, bieten sie wertvolle Einsichten und Herausforderungen.
Die Reise, um diese Zahlen zu verstehen, ist gleichzeitig eine Reise zu den fundamentalen Fragen der Mathematik und ihren Anwendungen in unserer modernen Welt.