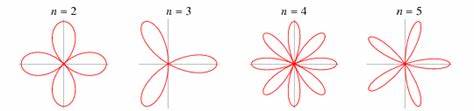
Die natürliche Welt steckt voller Formen und Strukturen, deren Schönheit weit über das Offensichtliche hinausgeht. Besonders Rosenblätter faszinieren mit ihren charakteristischen Formen, oft mit sanften Rundungen, aber ebenso mit spitzen Kanten und gerollten Rändern. Was auf den ersten Blick wie ein reines Produkt der Natur erscheint, offenbart bei näherer Betrachtung komplexe mathematische Prinzipien, die bisher in der Natur nie beobachtet wurden. Forscherinnen und Forscher haben durch eine Kombination aus theoretischer Analyse, Computermodellierung und Experimenten mit elastischen Materialien herausgefunden, dass die Form von Rosenblättern durch eine unerwartete Art von geometrischem Feedback gesteuert wird. Diese Entdeckung öffnet ein neues Fenster in unser Verständnis über Wachstumsprozesse und Morphogenese in der Pflanzenwelt.
Die Grundlage dieser Forschung bildet ein interdisziplinärer Zugang mit Elementen aus der Biophysik, Entwicklungsbiologie und Mathematik. Ziel war es, die Mechanismen zu entschlüsseln, die Rosenblättern ihre individuellen Formen verleihen. Besonders auffällig ist dabei die Art, wie die Ränder der Blätter nach außen rollen und spitze Enden bilden – eine Gestaltung, die durch komplexe mechanische Rückkopplungen während des Wachstums ermöglicht wird. Das Prinzip hinter diesem Phänomen ist eine Art geometrisches Feedback, bei dem die mechanischen Spannungen in den Zellen des Blattes das Wachstum selbst regulieren. Dies bedeutet, dass die plastischen und elastischen Eigenschaften des Gewebes das Zellwachstum nicht nur passiv begleiten, sondern aktiv beeinflussen.
Die Forscher entdeckten, dass sich durch diese rückgekoppelte Kontrolle die Auslenkungen an den Rändern verstärken, was zu den charakteristischen Spitzen und gewellten Strukturen führt. Um diese komplexen Vorgänge besser zu verstehen, wurden Experimente mit dehnbaren Kunststofffolien durchgeführt, die das Verhalten echter Blätter simulieren sollten. Die Folien wurden so modelliert und mechanisch beansprucht, dass sie ähnliche Formen wie Rosenblätter annahmen. Dabei zeigte sich, dass die mechanischen Rückkopplungen, die das Wachstum regulieren, zu den geförderten Wellen und Spitzen führen. Die theoretische Modellierung unterstützte diese Beobachtungen mit simulationsgestützten Analysen, welche mathematische Gleichungen aus der Elastizitätstheorie verwendeten.
Dieses Modell weist auf eine neue Art von geometrischem Feedback hin, die bisher in der Natur nicht identifiziert worden war. Die mathematischen Konzepte hinter der Formbildung von Rosenblättern sind nicht nur aus ästhetischer Sicht bemerkenswert, sondern liefern auch Einsichten, wie biologische Systeme komplexe, stabile Strukturen erzeugen können. Anders als einfache Wachstumsmuster, die eine gleichmäßige Ausdehnung annehmen, entsteht durch das Zusammenspiel von mechanischer Spannung und Wachstum eine dynamische Formgebung, die Variationen und Wiederholungen im Erscheinungsbild der Blätter zulässt. Diese Erkenntnisse haben weitreichende implications nicht nur für die Biologie, sondern auch für technische Anwendungen. Beispielsweise können die Prinzipien hinter der Formgebung von Rosenblättern Vorbild für neue Designstrategien in der Materialwissenschaft sein, in denen flexible und reaktionsfähige Oberflächen benötigt werden.
Auch in der Robotik oder der Entwicklung von weicheren, anpassungsfähigen Materialien könnten diese Feedback-Mechanismen Anwendung finden. Die Entdeckung betont außerdem die Bedeutung der Mathematik als universelles Werkzeug in den Naturwissenschaften. Sie erlaubt es, komplizierte natürliche Phänomene nicht nur zu beschreiben, sondern auch vorherzusagen und zu reproduzieren. Die Verbindung von Geometrie, Mechanik und Wachstumsdynamik bringt neue Perspektiven auf, wie Formen in lebenden Organismen entstehen und sich entwickeln. Zusammenfassend zeigt die Forschung, dass Rosenblätter weit mehr sind als nur dekorative Pflanzenteile.
Ihre Form ist Ergebnis eines präzisen Zusammenspiels zwischen biophysikalischen Mechanismen und mathematischen Prinzipien. Die Art, wie die Blattränder rollen und Spitzen bilden, stellt eine einzigartige Form von geometrischem Feedback dar, die die Schönheit in der Natur mit Ingenieurskunst verbindet. Diese außergewöhnliche mathematische Basis eröffnet neue Horizonte für das Verständnis von natürlichen Wachstumsprozessen und inspiriert zugleich innovative technische Lösungen. Wer sich für die verborgenen Muster und Regeln der Natur interessiert, findet in der Form der Rosenblätter ein faszinierendes Beispiel dafür, wie Mathematik und Biologie auf eindrucksvolle Weise zusammenwirken.