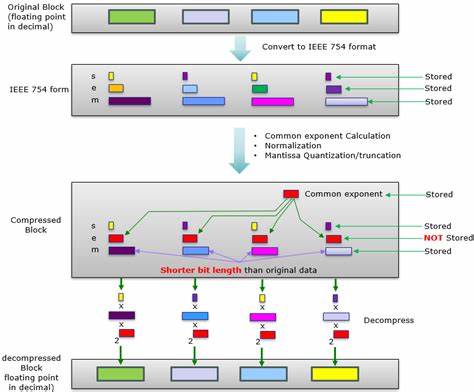
Die Speicherung und Verarbeitung von Gleitpunktzahlen ist in vielen Bereichen der Technik und Wissenschaft von zentraler Bedeutung. Besonders bei der Arbeit mit komplexen mathematischen Funktionen und umfangreichen Datenbeständen stellt sich die Frage, wie effektiv diese Zahlen komprimiert werden können, ohne ihre Genauigkeit zu verlieren. Diese Problematik gewinnt an Wichtigkeit, wenn Daten über Plattformen hinweg ausgetauscht oder umfassende Referenzimplementierungen getestet werden sollen. Doch wie klein kann man Gleitpunktzahlen tatsächlich machen, ohne dass die angeschlossenen Algorithmen oder Anwendungen beeinträchtigt werden? Gleitpunktzahlen umfassen in der Regel Formate wie 32-Bit-Single-Precision oder 64-Bit-Double-Precision. Je nach Anzahl der Bits sind sie in der Lage, eine große Bandbreite an Zahlenwerten darzustellen, darunter auch sehr kleine oder sehr große Zahlen.
Diese hohe Präzision ist jedoch ein zweischneidiges Schwert, denn je mehr Bits für die Darstellung benötigt werden, desto größer ist der Speicherbedarf - ein Faktor, der bei der Übertragung großer Datenmengen schnell zum Problem werden kann. Eine besonders interessante Herangehensweise an das Thema ist die Kompression der Ausgabedaten von mathematischen Funktionen. Beispielsweise erzeugt die Kosinusfunktion alle möglichen Ausgaben auf 32-Bit-Eingaben. Rein rechnerisch entspricht das 4.294.
967.296 verschiedenen Werten, die unkomprimiert etwa 16 Gigabyte Speicher erfordern würden. Im Zeitalter von Big Data und vernetzten Systemen ist so eine Datenmenge unpraktisch, nicht zuletzt wenn mehrere Plattformen die gleichen Referenzwerte benötigen. Die erste naive Lösung ist die Anwendung herkömmlicher Kompressionsalgorithmen wie Zstandard auf maximale Kompressionslevel. Obwohl hierdurch bereits eine Reduktion auf knapp unter 3 Gigabyte möglich ist, bleibt das Datenvolumen immer noch zu groß für einen praktischen, flexiblen Einsatz.
Das zeigt, dass einfache Kompression allein nicht ausreicht, um die Daten auf eine wirklich handhabbare Größe zu bringen. Um das Kompressionspotential weiter auszureizen, lohnt sich die Analyse der Struktur der Daten selbst. Über die Werte der Kosinusfunktion weiß man, dass viele aufeinanderfolgende Ausgaben nahe beieinander liegen, insbesondere im Definitionsbereich zwischen -1 und 1, der einen Großteil des Wertebereichs abdeckt. Dies legt nahe, dass Informationen über die Differenz zwischen den Ausgabewerten, sogenannte Delta-Codierung, eine effizientere Speicherung ermöglichen können. Die Praxis zeigt jedoch, dass dieser Ansatz allein oft scheitert.
Die Einführung von Delta-Codierung erhöht beispielsweise den durchschnittlichen Speicherbedarf sogar, was auf häufige und teils drastische Vorzeichenwechsel sowie große Schwankungen bei hohen Exponenten zurückzuführen ist. Diese Besonderheiten in der Verteilung der Werte wirken sich negativ auf die Effektivität traditionellen Delta-Codings aus. Ein weiterer Versuch stellt die Umwandlung der Mantissadifferenzen mithilfe von Variablen Längenkodierung (Varint) dar. Hierbei wird dank der Verwendung intelligenter Kodierungsmethoden wie Zig-Zag-Encoding versucht, kleine Differenzen besonders platzsparend abzulegen. Dennoch zeigt sich in der Praxis, dass dies die Speichergröße nicht signifikant reduziert und in einigen Fällen sogar eine Verschlechterung der Kompression bewirkt.
Ein alternatives, aussichtsreiches Vorgehen ist das Verknüpfen der Komprimierung mit domänenspezifischem Wissen und Metriken. So können beispielsweise XOR-Kodierungen zwischen aufeinanderfolgenden Ausgaben zu einer einigermaßen besseren Reduktion führen als Rohdaten-Kompression, indem sie Muster im binären Format sichtbar machen und dadurch für Kompressionsalgorithmen zugänglicher machen. Trotzdem bewegt sich die resultierende Datenmenge immer noch in Größenordnungen, die in der Praxis herausfordernd sind. Neben den hier beschriebenen Ansätzen gibt es vom Stand her auch Methoden wie fpzip, eine spezifische Kompressionssoftware für Fließkommadaten. Solche spezialisierten Tools sind in der Lage, durch die Ausnutzung von Eigenschaften der Gleitpunktdarstellung die Daten noch effizienter zu komprimieren.
Der Einsatz solcher Verfahren steht jedoch im Spannungsfeld zwischen Kompressionsrate, Rekonstruktionsgenauigkeit und Rechenaufwand, was die Auswahl der richtigen Technik stark von Anwendungsszenario und Zielsetzung abhängig macht. Ein zentraler Aspekt, der bei der Kompression von Gleitpunktdaten bislang nur selten ausreichend Beachtung gefunden hat, ist die Konsistenz und Reproduzierbarkeit von mathematischen Funktionen über verschiedene Plattformen hinweg. Gerade in Bereichen wie GPU-Computing oder beim Vergleich verschiedener Implementierungen von Standard-Bibliotheken kann die Abweichung in den Ergebnissen problematisch sein. Daher werden oft Referenzbibliotheken mit Soft-Float-Implementierungen verwendet, um sicherzustellen, dass Ergebnisse vorhersagbar und konsistent sind – dies führt jedoch wiederum zu sehr großen Datensätzen, die gespeichert und übertragen werden müssen. Die Kompression solcher Referenzwerte ist folglich nicht nur eine Speicherfrage, sondern betrifft bei weitem auch die Validität und Qualität der wissenschaftlichen oder technischen Prüfung.
Es steht also immer die Herausforderung im Raum, Speicherplatzersparnis, Verarbeitungsgeschwindigkeit und Genauigkeit unter einen Hut zu bringen. Generell ist zu beobachten, dass flüchtige Schwankungen wie Signenwechsel oder exponentielle Sprünge die bestehenden Kompressionsverfahren limitiert haben. Ein so hoher Anteil von komplexen Datenmustern in den Ergebnissen erfordert oftmals, dass innovative, maßgeschneiderte Algorithmen entwickelt werden, die sich gezielt auf die Eigenheiten der Gleitpunktarithmetik fokussieren. Diese Algorithmen müssten beispielsweise zwischen verschiedenen Zahlenbestandteilen (Mantisse, Exponent, Vorzeichen) differenzieren und adaptiv komprimieren. Zusammenfassend lässt sich feststellen, dass die Kompression von Gleitpunktdaten ein hochkomplexes Feld ist, das sowohl tiefergehende mathematische Kenntnisse als auch ein Verständnis für Datenstrukturen und Kompressionsalgorithmen erfordert.
Einfache Verfahren wie Standard-Kompression oder naive Delta-Codierung erreichen ihre Grenzen, sobald signifikante Variabilität im Datenbestand herrscht. Da eine vollständige Testung bei 64-Bit-Funktionen aufgrund der enormen Eingabemenge nahezu unmöglich ist, wird weiterhin nach einem pragmatischen Mittelweg gesucht, um Reproduzierbarkeit und Speicher- bzw. Übertragbarkeit der Ergebnisse praktikabel zu machen. Bislang ist das Ziel, die Daten von mehreren Gigabyte auf unter 500 Megabyte zu bringen, noch nicht erreicht – eine Voraussetzung dafür, solche umfangreichen Referenzdatenbanken bequem zwischen Systemen zu bewegen. Die zukünftige Entwicklung in diesem Bereich wird wahrscheinlich von der Kombination aus speziell designten Kompressionsalgorithmen, domänenspezifischem Fachwissen sowie potenziell neuen Repräsentationsformen für Gleitpunktzahlen geprägt sein.
Solche Innovationen könnten eine Revolution in der Art und Weise bringen, wie wissenschaftliche Daten erzeugt, gespeichert und validiert werden. Die Erforschung von effizienten Kompressionsverfahren für Gleitpunktwerte bleibt also eine spannende Zukunftsaufgabe mit großer Relevanz für verschiedene Forschungsgebiete und Industriestandorte weltweit. Die Herausforderung besteht darin, eine Balance zwischen Kompressionstiefe, Geschwindigkeit und Ergebnisgenauigkeit zu finden, die den praktischen Anforderungen gerecht wird. In Anbetracht der stetig wachsenden Datenmengen und der zunehmenden Verteilung der Verarbeitungssysteme wird die Bedeutung solcher Lösungen in der nahen Zukunft weiter steigen.