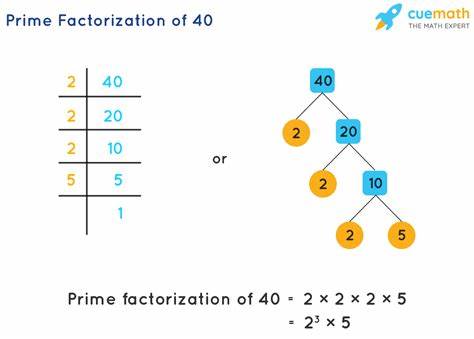
Die Primfaktorzerlegung zählt zu den fundamentalen Problemstellungen der Zahlentheorie und hat weitreichende Bedeutung in vielfältigen Bereichen wie Kryptographie, algorithmischer Forschung und maschinellem Lernen. Ein innovativer Ansatz, der aktuell verstärkt Aufmerksamkeit erhält, ist das Digit-Class Prime Product Framework, auch bekannt unter der Bezeichnung S(N,K)-Rahmenwerk. Dieses mathematische und algorithmische Framework ermöglicht die systematische Erzeugung und Bewertung von Primfaktorzerlegungen mit genau kontrollierbarer Komplexität und vielfältigen Anwendungsgebieten, insbesondere im Kontext moderner KI-Modelle. Das Digit-Class Prime Product Framework verdankt seinen Namen der präzisen Klassifikation von Primzahlen nach ihrer Ziffernlänge, welcher als Digit-Class bezeichnet wird. Mehrdimensional wird das Produkt von Primzahlen mit Faktoren aus verschiedenen Ziffernklassen systematisch betrachtet, was eine fein abgestufte Kontrolle über die Schwierigkeit und Struktur der zu erzeugenden Faktorisierungsprobleme erlaubt.
Die Parameter N und K in S(N,K) definieren dabei die maximale Anzahl von Primfaktoren sowie die erlaubten Digit-Classes, also die Ziffernlängen der zugelassenen Primzahlen. Der Kern des Frameworks besteht darin, Mengen von natürlichen Zahlen zu definieren, die sich als Produkte von bis zu N Primfaktoren zusammensetzen, wobei jeder Faktor einer bestimmten Ziffernklasse in K angehört. Durch diese Strukturierung lassen sich faktorisierungsbezogene Aufgaben nicht nur nach Größe, sondern auch nach Variabilität der Faktoren gezielt generieren, was für die algorithmische Benchmarking- und Lernprozess-Steuerung eine wichtige Grundlage schafft. Ein zentrales Merkmal des Frameworks ist die Einführung sogenannter Signaturen beziehungsweise ω-Vektoren, die die genaue Verteilung der Faktorlängen in einem Produkt beschreiben. Diese Signaturen ermöglichen es, die Varianz und Diversität der Faktoren zu quantifizieren, was sich direkt auf die Komplexität beim Zerlegen solcher Zahlen auswirkt.
Insbesondere lässt sich durch Entropiemessungen der Faktorenverteilung eine valide Einschätzung der Schwierigkeit für algorithmische sowie KI-basierte Zerlegungen erzielen. In praktischer Hinsicht kommt das Framework als Basis für umfangreiche Benchmark-Datensätze zum Einsatz, die unterschiedliche Schwierigkeitsgrade von einfachen bis hin zu extrem komplexen Faktorisierungsproblemen abdecken. Diese Datensätze werden sowohl für klassische Algorithmen wie die Pollard'sche Rho-Methode, den elliptischen Kurvenalgorithmus oder das Quadratische Sieb verwendet als auch zur Evaluierung und Schulung moderner neurosymbolischer Faktorisierungsmodelle. Die neurosymbolische Faktorisierung bildet einen hybriden Ansatz, der symbolische mathematische Methoden mit Deep Learning und verstärkendem Lernen verbindet. Die KI-Systeme werden dabei mit Schwierigkeiten trainiert, die vom Digit-Class Prime Product Framework kontrolliert werden.
So lernen Modelle nicht nur einzelne Schritte der Zerlegung, sondern auch komplexe Strategien, um Muster und Strukturen in riesigen Zahlräumen zu erkennen und effizient zu nutzen. Dieses Verfahren wird derzeit mit neuesten LLMs wie GPT-4 und spezialisierten neuronalen Netzwerken kombiniert, um Leistungssteigerungen und bessere Generalisierung auf unterschiedliche Problemgrößen und -typen zu erreichen. Durch die Integration mit Reinforcement-Fine-Tuning-Methoden wie OpenAI's RFT und GRPO (Group Relative Policy Optimization) verbessern sich die KI-Modelle signifikant in Bezug auf Genauigkeit, Vollständigkeit und logische Stringenz der Zerlegungen. Insbesondere lässt sich bei mittleren bis hohen Schwierigkeitsgraden eine starke Steigerung der Erfolgsraten beobachten, was die Effektivität des Frameworks in Kombination mit modernen KI-Technologien eindrucksvoll demonstriert. Ein weiteres zukunftsträchtiges Anwendungsfeld sind quantenresistente Kryptographieaufgaben.
Das Digit-Class Prime Product Framework erlaubt die gezielte Generierung von Faktorisierungsproblemen, die auch für Quantenalgorithmen eine besondere Herausforderung darstellen. Dies geschieht durch die Einbindung von Gitterproblemen und komplexen Signaturmustern, die auf postquantenkryptographische Sicherheit abzielen. Hierdurch lassen sich realitätsnahe Testsets formulieren, die nicht nur klassische, sondern auch neuartige Quantensicherheitsmodelle prüfen können. Die mathematische Tiefe des Frameworks basiert auf weitreichenden Konzepten aus der algebraischen Strukturtheorie, Monoid- und Kategorientheorie. Die Faktorisierung im Rahmen von S(N,K) wird als Teil einer abelschen freien Monoide betrachtet, deren Elemente durch Vektor-Ausdrücke und Signaturen repräsentiert werden.
Die Verschmelzung mit kategorialen Prinzipien eröffnet neue Perspektiven zur Modellierung von Faktorierungsprozessen als morphismische Beziehungen in symmetrisch monoidalen Kategorien – ein Ansatz, der in der theoretischen Informatik und modernen Mathematik zunehmend an Bedeutung gewinnt. Praktisch unterstützt das Projekt ein breites Spektrum von Softwarewerkzeugen, die von der effizienten Primzahlerzeugung über leistungsfähige Visualisierungstools bis hin zu dreistufigen Verifikationssystemen reichen. Insbesondere die modulierbare Zwischenverifikation erlaubt es, factorization steps in Echtzeit automatisiert auf Korrektheit zu prüfen, was aufwendige manuelle Validierungen überflüssig macht und die Zuverlässigkeit von Ergebnisprotokollen deutlich steigert. Die Softwarelandschaft umfasst auch Schnittstellen zur Parquet- und JSON-basierten Datenspeicherung, welche große Datenmengen effizient handhaben können und gleichzeitig den Anforderungen moderner Machine-Learning-Pipelines gerecht werden. So können Entwickler und Forscher Benchmarks direkt in ML-kompatiblen Formaten laden, trainieren und auswerten.
Zu den innovativen Highlights zählen auch quantenalgorithmische Erweiterungen, die das Framework um fortschrittliche Varianten von Shor's Algorithmus mit Ziffernklassen-bedingten Einschränkungen ergänzen. Diese ermöglichen eine theoretische Verbesserung der Laufzeitkomplexität und bieten damit neues Fundament für die Erforschung quantenoptimierter Primfaktorzerlegung. Abschließend präsentiert sich das Digit-Class Prime Product Framework als zukunftsweisende Schnittstelle zwischen klassischer Zahlentheorie, algorithmischer Forschung und Künstlicher Intelligenz. Es schafft eine strukturierte und kontrollierte Umgebung zum Generieren, Testen und Bewerten von Faktorisierungsaufgaben, die sowohl die Grenzen aktueller Rechner als auch neuronaler Modelle herausfordern. Durch die Verknüpfung tiefgreifender mathematischer Konzepte mit praktischer KI-Integration bietet es vielfältige Möglichkeiten für Forscher, Entwickler und Pädagogen, um komplexe mathematische Fähigkeiten systematisch zu fördern und innovative Sicherheitslösungen zu erforschen.
Das Framework steht als Open-Source-Projekt mit umfangreicher Dokumentation, leistungsfähigen Beispielskripten und einer aktiven Community zur Verfügung. Es lädt zur Mitwirkung und Weiterentwicklung ein, um die Grenzen in der Primfaktorzerlegung und deren Anwendungen künftig noch weiter zu verschieben.