Die Kraft des Trampolins: Rekursion in Iteration verwandeln für effizientes Python-Programmieren

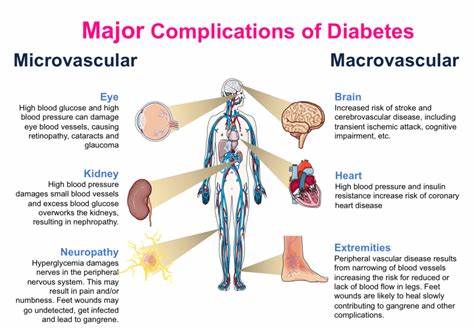
Rekursion gilt als eines der grundlegenden Prinzipien der Programmierung und ermöglicht elegante Lösungen für komplexe Probleme. Doch trotz der Konstruktivität und Lesbarkeit rekursiver Funktionen kann ihre Anwendung einige Herausforderungen mit sich bringen, insbesondere in Sprachen wie Python, die keine native Optimierung für Endrekursion bieten. Das Phänomen des Stack-Überlaufs durch zu viele Funktionsaufrufe ist dabei eine häufige Sorge. Genau an dieser Stelle gewinnt das Konzept des Trampolins an Bedeutung – eine Technik, mit der sich rekursive Algorithmen in iterative umwandeln lassen, ohne dabei die Klarheit der ursprünglichen Struktur zu verlieren. Diese Methode stellt eine geschickte Möglichkeit dar, um die Stack-Erschöpfung zu verhindern und zugleich die Leistungsfähigkeit der Programme zu steigern.

Um das Trampolinprinzip zu verstehen, ist es wichtig, zunächst die Funktionsweise von Funktionsaufrufen und deren Umgang mit dem Aufruf-Stack zu betrachten. Jedes Mal, wenn eine Funktion aufgerufen wird, legt die Laufzeitumgebung einen neuen Rahmen – auch als Execution Frame bezeichnet – auf den Stack. Dieser Rahmen speichert lokale Variablen, Rücksprungadressen und andere relevante Informationen. Sobald die Funktion beendet ist, wird der Rahmen entfernt und die Kontrolle an die aufrufende Funktion zurückgegeben. Bei einfachen oder flachen Funktionsaufrufen ist dies unproblematisch.

Doch bei tiefen oder unendlichen Rekursionen wächst der Stack rapide an und führt zu Speicherengpässen. Ein bewährtes Muster zur Vermeidung dieser Probleme heißt Endrekursion bzw. Tail-Call-Optimierung. Dabei wird ein Funktionsaufruf als letzter Schritt innerhalb einer Funktion ausgeführt, sodass keine weiteren Operationen nach dem Rückruf erforderlich sind. Einige Programmiersprachen wie Scheme oder Haskell unterstützen diese Optimierung direkt, indem sie den aktuellen Frame auf dem Stack recyceln, wodurch sich die Anzahl der Aufrufrahmen nicht erhöht.

Leider makiert Python keinen Tail Call, sodass auch endrekursive Aufrufe jeden Funktionsrahmen auf den Stack legen und ein Stack-Overflow droht, wenn die Rekursion zu tief wird. Das Trampolin-Konzept stellt eine elegante Lösung dar, die diese Limitierung in Python überwindet. Es funktioniert wie ein „Sprungbrett“, das Kontrolle und Argumente zwischen den Funktionsaufrufen vermittelt und dabei hilft, den Aufruf-Stack nicht anschwellen zu lassen. Die zentrale Idee besteht darin, nicht direkt rekursiv aufzurufen, sondern stattdessen Anweisungen in Form von speziellen Rückgabewerten – sogenannten „Call“- oder „Result“-Instruktionen – zurückzugeben. Diese Instruktionen werden von einer übergeordneten Schleife, dem eigentlichen Trampolin, ausgewertet.

Die Schleife interpretiert die angedeuteten nächsten Aufrufe und sorgt so für die iterative Abwicklung, ohne neue Stack-Rahmen zu erzeugen. In der praktischen Umsetzung bedeutet das, dass eine Funktion, welche eine rekursive Endbedingung oder einen weiteren Aufruf hat, nicht direkt den rekursiven Funktionsaufruf tätigt, sondern stattdessen ein Tupel oder ein ähnliches Datenobjekt zurückgibt, das beschreibt, welche Funktion als Nächstes mit welchen Parametern auszuführen ist. Das Trampolin verarbeitet diese Anweisung, führt die Funktion aus und wiederholt diesen Vorgang, bis ein endgültiges Ergebnis geliefert wird. Erst dann verlässt es die Schleife und gibt den Wert zurück, womit die Funktionen nicht gestapelt, sondern sequentiell abgearbeitet werden. Ein exemplarisches Beispiel hierfür ist die Berechnung der Fakultät.

Die klassische rekursive Implementierung zeigt eine klare, verständliche Struktur, leidet aber unter Performance- und Speicherproblemen bei größeren Eingabewerten, da für jeden rekursiven Aufruf ein neuer Stack-Rahmen aufgehoben wird. Um dies zu optimieren, lässt sich die Funktion so anpassen, dass sie die letzte Operation als Rückgabe einer Call-Anweisung fasst, die vom Trampolin verarbeitet wird. Dadurch wird die Rekursion quasi in eine Schleife umgewandelt. Dabei beginnt die überarbeitete Fakultätsfunktion mit einer Akkumulationsvariable, die das Zwischenergebnis hält. Bei Erreichen der Basisbedingung wird das Ergebnis als Resultat-Anweisung an das Trampolin geschickt.

Im rekursiven Fall hingegen generiert die Funktion eine Call-Anweisung, die einen weiteren Funktionsaufruf mit den aktualisierten Argumenten beinhaltet. Das Trampolin übernimmt diesen Aufruf und wiederholt ihn so lange, bis das finale Ergebnis vorliegt. Somit wird der Stack nie überbeansprucht – die Funktion läuft im Wesentlichen iterativ ab – ohne jedoch an Lesbarkeit oder Modularität einzubüßen. Die Umsetzung des Trampolins in Python ist relativ simpel und erfordert nur wenige Zeilen Code. Die Kernkomponenten sind zwei Hilfsfunktionen, die Call- und Resultat-Anweisungen erzeugen, sowie eine Dekoratorfunktion, die eine Funktion so umhüllt, dass sie vom Trampolin ausgeführt wird.

Die Dekoratorfunktion verwaltet die iterative Schleife, in der die aufeinanderfolgenden Funktionsaufrufe abgewickelt werden. Die Flexibilität dieser Konstruktion ermöglicht es, eine Vielzahl von endrekursiven Funktionen ohne großen Mehraufwand umzubauen. Der Einsatz des Trampolins bietet Vorteile, vor allem in Szenarien, in denen die einfache Umwandlung von Rekursion in Schleifen nicht praktikabel ist. Beispielsweise können Funktionen komplexe Kontrollstrukturen mit verschachtelten Schleifen besitzen, in denen eine einfache Schleifenersetzung durch continue-Anweisungen schwer umzusetzen ist. Hier kann das Trampolin helfen, indem es die rekursive Struktur bewahrt, aber gleichzeitig Laufzeitprobleme durch Stack-Überläufe vermeidet.

Dennoch ist der Trampolin-Ansatz kein Allheilmittel. Die einfachste und performanteste Methode zur Umwandlung von Rekursion in Iteration bleibt oft die sogenannte Simple Method, die den rekursiven Aufruf vollständig durch inneren Zustand und Schleifen ersetzt. Diese Methode ist jedoch bei verschachtelten oder komplexen Schleifenbedingungen weniger intuitiv. Zudem neigen Entwickler meist dazu, bei Endrekursionen gleich die Simple Method anzuwenden, da sie einen direkten, nachvollziehbaren Iterationscode erzeugt. Das Verständnis des Trampolin-Konzepts ist dennoch für jeden Programmierer von Vorteil.

Es gilt als ein wichtiges Element im Werkzeugkasten der funktionalen Programmierung und öffnet Türen zu noch weiterführenden Techniken wie der sogenannten Continuation-Passing Style (CPS) Programmierung, die komplexe Kontrollflüsse und Optimierungen ermöglicht. Die Kenntnis dieses Prinzips vermittelt ein tieferes Verständnis für die Interna von Funktionsaufrufen und ist eine solide Grundlage für den Umgang mit rekursiven Strukturen in Sprachen ohne native Tail-Call-Optimierung. Wer sich mit Python beschäftigt, wird feststellen, dass der Trampolin-Ansatz auch in der Python-Community auf Interesse stößt. Fachautoren wie Kyle Miller haben bereits ausführliche Ausarbeitungen präsentiert, die weitere Anwendungsfälle und Implementierungsvarianten beleuchten. Ebenso ermöglichen Tools wie der Online Python Tutor, die Ausführungen Schritt für Schritt zu visualisieren und die Funktionsweise von klassischen, endrekursiven und trampoline-basierten Funktionen anschaulich zu machen.

Zusammenfassend lässt sich sagen, dass das Trampolinprinzip eine clevere Technik ist, die funktionale Schönheit und pragmatische Notwendigkeiten verbindet. Es erlaubt die Nutzung einer rekursiven Denkweise, ohne die systembedingten Grenzen des Aufruf-Stacks zu überschreiten. Für Entwickler, die sich mit der Optimierung rekursiver Algorithmen und der Verbesserung der Performance beschäftigen, eröffnet das Trampolin eine interessante Alternative neben herkömmlichen Iterationsmethoden. Nicht zuletzt trägt das Verständnis dieser Methode dazu bei, die Konzepte moderner Programmierparadigmen besser zu durchdringen und den eigenen Programmierstil zu erweitern.