Das Verständnis von maschinellem Lernen beginnt oft mit einem einfachen linearen Modell: der linearen Regression. Sie stellt die Idee dar, komplexe Zusammenhänge in Daten durch eine gerade Linie zu beschreiben. Von dort aus entfaltet sich ein faszinierender Weg, der von der Methode der kleinsten Quadrate bis hin zu modernen Optimierungsalgorithmen wie dem Gradientenabstieg führt – eine Entwicklung, die letztendlich die Basis für zahlreiche Anwendungen in der künstlichen Intelligenz bildet. Lineare Regression bedeutet im Wesentlichen, eine Gerade so an eine Menge von Datenpunkten anzupassen, dass sie den Trend am besten widerspiegelt. Im Kontext von Hauspreisen zum Beispiel nimmt man an, dass die Quadratmeterzahl eines Hauses den Preis maßgeblich beeinflusst.
Wenn man diese Beziehung grafisch darstellt, zeigt sich oft ein aufsteigender Trend: größere Häuser sind tendenziell teurer. Um eine verlässliche Vorhersage zu erhalten, muss man also eine Gerade finden, die möglichst nah an den tatsächlichen Verkaufspreisen liegt. Dabei spielen zwei Werte eine entscheidende Rolle: die Steigung und der Achsenabschnitt der Geraden. Die Steigung beschreibt, wie stark sich der Preis pro zusätzlichem Quadratmeter erhöht – also gewissermaßen den „Preis pro Quadratmeter“. Der Achsenabschnitt hingegen ist der Basispreis, der theoretisch bei einer Wohnfläche von null Quadratmetern startet, was zwar keinen praktischen Wert besitzt, jedoch die Linie im Koordinatensystem verschiebt.
Die Herausforderung ist nun, die optimalen Werte für Steigung und Achsenabschnitt zu finden, sodass die Gerade die vorliegenden Daten bestmöglich modelliert. Um dies zu bewerten, muss man messen, wie stark die Vorhersagen von den tatsächlichen Beobachtungen abweichen. Diese Abweichungen nennt man Fehler bzw. Residuen. Ein einfacher Weg, den Gesamtfehler einer Linie zu messen, ist die Summe der absoluten Differenzen zwischen den vorhergesagten und tatsächlichen Hauspreisen.
Das klingt zunächst plausibel, da jede Abweichung – ob nach oben oder unten – gleich behandelt wird. Allerdings hat diese Methode einige Nachteile, vor allem, wenn es um große Fehler geht. Große Ausreißer können bei der absoluten Fehlerberechnung unterschätzt werden. So könnten zwei mittelgroße Fehler zusammen dieselbe Bewertung erhalten wie ein einziger großer Fehler. Dieses Problem lässt sich umgehen, indem man statt der absoluten Differenzen die quadrierten Fehler verwendet – das heißt, man nimmt jede Abweichung, quadriert sie und summiert diese Werte auf.
Das Quadrieren hat den Effekt, große Fehler exponentiell stärker zu gewichten als kleine. Ein Fehler von 50.000 Euro wird so mit 2,5 Millionen bestraft, während ein Fehler von 10.000 Euro nur mit 100 Millionen berechnet wird. Das motiviert unser Modell, große Fehler zu minimieren und stattdessen konstante Genauigkeit über alle Datenpunkte zu erreichen.
Diese Vorgehensweise ist bekannt als die Methode der kleinsten Quadrate (englisch: Least Squares). Sie sorgt für stabile und eindeutige Lösungen, denn die Fehlerfunktion ergibt eine glatte, nach unten geöffnete Parabel. Auf diesem Fehlerlandscape gibt es genau einen Punkt mit minimalem Fehler – die optimale Gerade. Anders verhält es sich bei der Nutzung der absoluten Fehler, die zu einer Fehlerlandschaft mit Ecken und Kanten führt. Hier kann es mehrere gleichwertige Lösungen geben, wodurch es unsicher wird, welche Gerade die tatsächliche beste ist.
Aus diesem Grund bevorzugen viele maschinelle Lernverfahren die Methode der kleinsten Quadrate. Die Suche nach der optimalen Gerade erfolgt also durch die Minimierung der Fehlerfunktion. Vollständig das Ergebnis durch Ausprobieren aller möglichen Kombinationen von Steigung und Achsenabschnitt zu finden, ist jedoch nicht praktikabel. Die Anzahl der Möglichkeiten ist unendlich und schon bei wenigen Parametern rechnet sich das schnell zu einer enormen Aufgabe. Um das Problem effizient zu lösen, nutzt man mathematische Optimierungsverfahren.
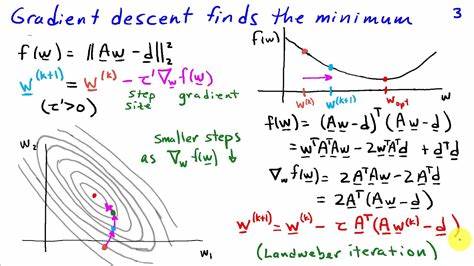
Eine der wichtigsten Techniken heißt Gradientenabstieg. Dabei begibt man sich gedanklich auf einen Berg und sucht den tiefsten Punkt im Tal, wo der Fehler minimal ist. Statt aus dem Stand alles zu testen, geht man Schritt für Schritt in die Richtung, die am stärksten nach unten führt. Konkret bedeutet das, dass man anfangs mit einer zufälligen Gerade startet und dann berechnet, wie sich die Fehlerfunktion ändert, wenn man Steigung und Achsenabschnitt ein kleines bisschen anpasst. Diese Änderungsrate nennt man Ableitung oder „Gradient“.
Sie zeigt an, in welche Richtung sich der Fehler erhöht oder verringert. Führt man die Anpassung bewusst in die entgegengesetzte Richtung der Ableitung aus, wandert die Lösung Stück für Stück in die Richtung des geringsten Fehlers. Wiederholt man diesen Prozess oft genug, nähert man sich der optimalen Gerade immer weiter an. Die Geschwindigkeit, mit der man sich zur Lösung bewegt, wird Lernrate genannt. Der Gradientenabstieg funktioniert besonders gut mit der Methode der kleinsten Quadrate, da diese Fehlerfunktion glatt und differenzierbar ist.
Die Kalkulation der Ableitungen ist einfach und liefert klare Signale, wie man seine Schätzwerte verbessern kann. In der Praxis kann man den traditionellen Gradientenabstieg noch weiter verfeinern. Besonders in Fällen mit sehr großen Datensätzen oder komplexen Modellen nutzt man statt des standardmäßigen Gradientenabstiegs eine Variante namens stochastischer Gradientenabstieg. Dabei werden jeweils nur kleine Datenmengen („Mini-Batches“) für jeden Schritt verwendet, was die Rechenzeit reduziert und gleichzeitig die Konvergenz fördert. Die Prinzipien, die bei der linearen Regression und dem Gradientenabstieg Anwendung finden, sind grundlegend für viele maschinelle Lernmodelle, einschließlich tiefgehender neuronaler Netze.
Hier sind ebenfalls Parameter anzupassen, um eine Fehlerfunktion zu minimieren, wobei der Gradientenabstieg in verschiedenen Varianten die treibende Kraft hinter dem Lernprozess ist. Ein tieferes Verständnis der mathematischen Hintergründe ist dabei ebenso hilfreich wie das intuitive Bild von „Schritte in die richtige Richtung machen“. Beides vereint lässt komplexe Algorithmen greifbar werden und erleichtert die Implementierung und erfolgreiche Anwendung in der Praxis. Zusammenfassend lässt sich sagen, dass der Weg von der Methode der kleinsten Quadrate zum Gradientenabstieg ein Meilenstein auf dem Gebiet des maschinellen Lernens ist. Er zeigt, wie aus einfachen mathematischen Prinzipien leistungsfähige Werkzeuge entstanden sind, mit denen es möglich ist, aus Daten zuverlässige Vorhersagen zu erstellen und immer bessere Modelle zu entwickeln.
Ob bei Immobilienpreisen, Finanzprognosen oder Spracherkennung: Die Fähigkeit, Fehler zu messen, zu bewerten und optimiert zu minimieren, ist das Herz moderner datengetriebener Entscheidungen. Dabei ist der Gradientenabstieg das Werkzeug, das diese Entwicklung beschleunigt und erst so vielseitig einsetzbar macht. Maschinelles Lernen lebt von der Balance zwischen mathematischer Eleganz und praktischer Umsetzbarkeit. Mit den Techniken, die sich aus der Methode der kleinsten Quadrate und dem Gradientenabstieg ableiten, eröffnen sich endlose Möglichkeiten, Daten zu verstehen und nutzbringend einzusetzen.