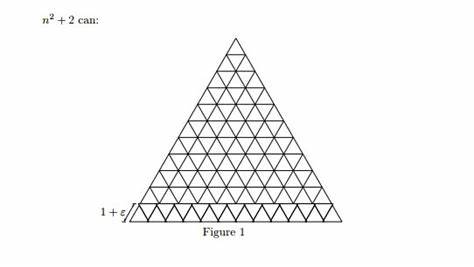
In der Welt der Mathematik dominieren oft umfangreiche Beweise, komplexe Formeln und ausführliche Erklärungen. Nun stellt sich jedoch die Frage: Wie kurz kann ein mathematischer Artikel sein und dennoch als wissenschaftliche Publikation gelten? Diese Frage beantworteten im Jahr 2004 der renommierte Mathematiker John Conway und sein Kollege Alexander Soifer auf eine höchst ungewöhnliche Weise. Sie stellten mit einem Artikel, der nur aus zwei Worten besteht, einen verblüffenden Weltrekord auf und sorgten damit für Aufsehen in der mathematischen Gemeinschaft. Die Geschichte hinter diesem außergewöhnlichen Artikel beginnt an der angesehenen Princeton University, wo Conway und Soifer gemeinsam an mathematischen Problemen arbeiteten. Am 28.
April 2004 reichten sie beim American Mathematical Monthly, einer der renommiertesten mathematischen Fachzeitschriften, eine Arbeit ein, die gerade einmal zwei Worte enthielt, nämlich „n2 + 2 can“, begleitet von zwei Zeichnungen, die ihre Argumentation visuell unterstützten. Diese Einreichung war nicht nur ungewöhnlich sparsam im sprachlichen Umfang, sondern auch eine bewusste Provokation und ein Experiment in Sachen wissenschaftlicher Kommunikation. Die Reaktion des American Mathematical Monthly war zu Beginn eher skeptisch. Die Redaktion war irritiert und wusste zunächst kaum, wie mit einem derart kurzen Beitrag umzugehen sei. Eine Mitarbeiterin der Zeitschrift schrieb Conway und Soifer zurück, dass ein Artikel von nur zwei Wörtern nicht den Ansprüchen genügt, die ein guter Beitrag für das Monthly haben sollte.
Eine kurze Erklärung oder etwas mehr Text zur Einordnung wären notwendig, hieß es. Das spiegelte die traditionelle Auffassung wider, dass Qualität und Umfang in einem gewissen Maße zusammenhängen und dass ein allzu knapper Text kaum ausreichend sei, ein mathematisches Problem angemessen zu präsentieren. Doch Conway blieb unbeirrt. Als er von der Rückmeldung hörte, meinte er lakonisch: „Nicht zu früh aufgeben.“ Diese Haltung spiegelte den Geist der beiden Mathematiker wider, die an die Substanz und Aussagekraft ihres Beitrags glaubten, unabhängig von dessen Umfang.
So antworteten sie auf die Kritik mit einem kurzen, aber pointierten Einspruch. Sie argumentierten, dass Quantität nicht zwangsläufig Qualität bedeute und dass ihr Beitrag eine offene Fragestellung formulierte und zwei visuelle „Beweise“ vorstellte, die als „behold-style“ bezeichnet wurden – eine Art der mathematischen Argumentation, bei der der Beweis mehr über das Ansehen und das Augenscheinliche vermittelt wird, anstatt in langen formalen Sätzen dargestellt zu werden. Trotz ihres Einspruchs blieb die Redaktion des American Mathematical Monthly zurückhaltend. Die Antwort vom Chefredakteur Bruce Palka unterstrich, dass die Zeitschrift normalerweise zwei Arten von Publikationen akzeptiert: ausführliche Artikel und kürzere sogenannte Notes. Ein Beitrag von zwei Wörtern allerdings entsprach weder den Anforderungen an einen Artikel noch an eine Note.
Stattdessen bot die Redaktion den Mathematikern an, ihren Beitrag als sogenannte „boxed filler“ zu veröffentlichen – kleine Textbausteine, die dazu dienen, Leerstellen in der Zeitschrift aufzufüllen. Obwohl dies einen gewissen Statusverlust bedeutete, stimmten Conway und Soifer schließlich zu. Im Januar 2005 erschien damit der kürzeste wissenschaftliche Vortrag in der Geschichte der Mathematik in einer anerkannten Fachpublikation. Der Rekord selbst ist faszinierend, nicht nur wegen des spektakulär knappen Charakters des Beitrags, sondern auch, weil er auf ungewöhnliche Weise die Grenzen der wissenschaftlichen Kommunikation austestet und das Verhältnis von Form und Substanz neu definiert. Diese Episode zeigt, dass Mathematik nicht nur Zahlen und Formeln bedeutet, sondern auch eine kreative und experimentelle Komponente besitzt.
Die beiden Mathematiker stellten mit ihrem rekordverdächtigen Beitrag die konventionellen Erwartungen in Frage und forderten dazu auf, über die Grenzen des Üblichen hinauszudenken. Der „zwei-Wort-Artikel“ wurde so zu einem Symbol für innovative Ansätze und die spielerische Seite der Wissenschaft. Darüber hinaus regt die Geschichte zu einer tieferen Diskussion über die Rolle von Publikationen in der Wissenschaft an. In einer Zeit, in der ein wachsender Publikationsdruck herrscht und quantitative Messgrößen wie die Anzahl der Veröffentlichungen oder Zitationen dominieren, mahnt das Beispiel von Conway und Soifer dazu, auch auf Qualität und originelle Ideen zu achten, unabhängig von deren äußeren Form. Neben dem Beitrag mit nur zwei Worten gibt es noch weitere bemerkenswerte Kurzartikel in der Wissenschaftsgeschichte.
Zum Beispiel veröffentlichte der berühmte Mathematiker John Nash eine Masterarbeit mit nur 26 Seiten und einem minimalen Literaturverzeichnis. Solche Beispiele zeigen, dass wissenschaftliche Exzellenz nicht an Umfang gemessen wird. Vielmehr zählt die Tiefe der Idee und ihr Einfluss auf die weitere Forschung. Das Phänomen der extrem kurzen Veröffentlichungen findet sich auch in anderen Bereichen. Zum Beispiel sind berühmte Aphorismen oder poetische Werke reduziert auf wenig Text, doch durch ihre Prägnanz und Konzentration erzeugen sie immense Wirkung.
Ähnlich verhält es sich mit dem mathematischen Kurzartikel von Conway und Soifer, der trotz seiner Kürze ein komplexes Problem adressiert und Diskussionen anregt. In der heutigen digitalen Ära, in der Informationen schnell konsumiert und verbreitet werden, gewinnt die Fähigkeit, Inhalte prägnant auszudrücken, zunehmend an Bedeutung. Die Herausforderung besteht darin, zwischen Reduktion und Wertverlust abzuwägen und die Essenz eines Themas zu erfassen, ohne dabei an Tiefe einzubüßen. Der bekannt gewordene Fall des kürzesten mathematischen Artikels leistet in diesem Zusammenhang einen wertvollen Beitrag zur Reflexion über Kommunikationsstrategien und die Grenzen von Wissenschaftspublikationen. Die Veröffentlichung von Conway und Soifer wird daher nicht nur als eine kuriose Anekdote betrachtet, sondern als eine Einladung zu einer selbstkritischen Überprüfung wissenschaftlicher Praxis und als Inspiration, mutig neue Wege zu gehen.
Gerade in der Mathematik, einem Fachgebiet, das als besonders streng und formal gilt, zeigt dieses Beispiel, dass Originalität und Humor durchaus ihren Platz haben. Die Öffentlichkeit und Medienschaffende nahmen dieses Ereignis auch mit Interesse auf, was die Brücke zwischen Fachwelt und Laien schlug. Die Geschichte des kürzesten mathematischen Artikels wurde vielfach erzählt und illustriert, wie Wissenschaft mit überraschenden und unkonventionellen Mitteln faszinieren und begeistern kann. Letztlich hält der Fall von John Conway und Alexander Soifer eine wichtige Lektion bereit: Wissenschaft lebt nicht nur von der Länge und Komplexität von Texten, sondern vor allem von Kreativität, Klarheit und dem Mut, bestehende Normen zu hinterfragen. Dieser minimalistische Beitrag öffnet das Tor dazu, Mathematik nicht als trockene Sammlung von Fakten, sondern als lebendige und stets wandelbare Disziplin zu verstehen.
Insgesamt zeigt die Geschichte des zweifachen Wortartikels eindrucksvoll, wie man mit wenigen Worten eine nachhaltige Wirkung erzielen und sogar einen Weltrekord aufstellen kann. Sie erinnert daran, dass manchmal weniger tatsächlich mehr ist – auch in der hochkomplexen Welt der Mathematik.