Im Zeitalter der Digitalisierung und vernetzten Kommunikation ist die Sicherheit von Daten entscheidender denn je. Der Diffie-Hellman-Schlüsselaustausch gilt seit Jahrzehnten als ein Meilenstein der kryptographischen Verfahren, der es ermöglicht, geheime Schlüssel über unsichere Kanäle auszutauschen. Doch bei genauerer Betrachtung und im Lichte moderner mathematischer Erkenntnisse wird klar: Es gibt eigentlich kein „Diffie-Hellman“ ohne elliptische Kurven – das sogenannte Elliptic Curve Diffie-Hellman (ECDH) ist die wahre Grundlage für sichere und effiziente Schlüsselaustauschverfahren heute. Doch warum ist das so? Was macht elliptische Kurven so besonders und warum sind andere Gruppen, die wir theoretisch für Diffie-Hellman verwenden könnten, weniger geeignet? Diese und weitere Fragen sollen im Folgenden auf anschauliche Weise beantwortet werden. Zunächst zum klassischen Diffie-Hellman-Verfahren: Dieses basiert auf mathematischen Gruppen.
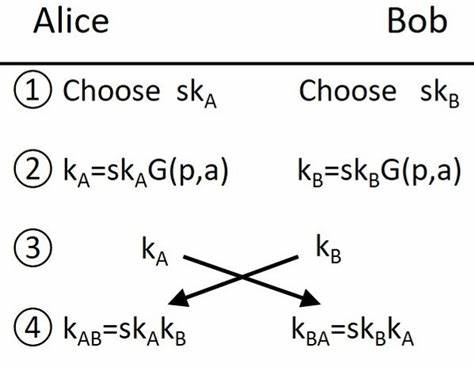
Eine Gruppe ist ein abstraktes Konstrukt aus der Mathematik, in der man eine Menge von Elementen mit einer Verknüpfung (Operation) versehen hat, die bestimmten Regeln folgt. Für Diffie-Hellman wird ein Element gewählt, aus dem man durch wiederholte Anwendung der Gruppenoperation – man spricht hier von „Exponentiation“ – öffentliche Schlüssel berechnet. Ein Teilnehmer wählt dabei einen privaten Schlüssel (eine Zahl) und berechnet daraus seinen öffentlichen Schlüssel, der dann mit dem öffentlichen Schlüssel des Partners kombiniert wird, um einen gemeinsamen geheimen Schlüssel zu erzeugen. Das Grundprinzip ist elegant und grundsätzlich auf jede Gruppe übertragbar. Die Frage ist allerdings, welche Gruppen überhaupt in der Praxis sinnvoll sind.
Natürlich könnte man theoretisch jede endliche Gruppe wählen. Warum dann nicht beispielsweise die Monstergruppe, eine der größten endlichen einfachen Gruppen, oder irgendeine andere exotische mathematische Struktur? Die Antwort liegt im Zusammenspiel von Effizienz, Sicherheit und der Struktur dieser Gruppen. Im klassischen Diffie-Hellman wird oft die multiplikative Gruppe der Einheiten modulo einer großen Primzahl verwendet. Diese Gruppe ist zyklisch und gut erforscht, allerdings wird das Verfahren durch ausgeklügelte Algorithmen zur Berechnung diskreter Logarithmen bedroht, die auf großen Zahlen basieren. Je größer die Primzahl, desto höher die Sicherheit, aber auch größer der Rechenaufwand.
Daher wird hier ein Limitation in der Skalierbarkeit deutlich. Elliptische Kurven bieten an dieser Stelle einen entscheidenden Vorteil. Bei elliptischen Kurven handelt es sich um algebraische Kurven, die mit einer besonderen mathematischen Struktur versehen sind, die eine Gruppeneigenschaft erlauben, aber mit deutlich weniger Elementen dieselbe Sicherheit bieten. Das bedeutet, dass bei wesentlich kleinerer Schlüssellänge die gleiche oder sogar höhere Sicherheit erreicht werden kann. Die Geheimhaltung beruht dabei auf dem sogenannten diskreten Logarithmusproblem auf elliptischen Kurven, das bis heute deutlich schwerer zu lösen ist als seine Pendants in anderen Gruppen.
Die Wahl elliptischer Kurven rührt also nicht von einem Zufall oder einer Laune her, sondern aus tiefen mathematischen und praktischen Überlegungen. Die Strukturen der elliptischen Kurven sind besonders robust gegenüber Angriffen, die auf die Effizienz der Exponentiationen und diskrete Logarithmen abzielen. Gleichzeitig sind sie hervorragend für moderne Computerumgebungen geeignet, da die Rechenoperationen relativ kompakt und effizient sind. Um noch tiefer zu verstehen, warum elliptische Kurven unverzichtbar sind, lohnt es sich, einen Blick auf die moderne abstrakte Mathematik zu werfen – speziell auf die Kategorien- und Gruppentheorie. In der Gruppentheorie betrachtet man Gruppen immer „bis auf Isomorphie“, das heißt, Gruppen, die strukturell identisch sind, werden als gleich angesehen.
Hierbei zeigt sich, dass die „klassischen“ Gruppen, die man für Diffie-Hellman verwenden könnte, aus Sicht der Mathematik grundsätzlich nicht unterscheidbar sind. Somit reicht diese Betrachtungsweise nicht aus, um private und öffentliche Schlüssel wirklich auseinanderzuhalten oder gar zu sichern. Deshalb betrachtet man Gruppenobjekte in Kategorien anderer mathematischer Strukturen, also sogenannte algebraische Gruppen, die nicht nur abstrakte Gruppen sind, sondern in einer Kategorie leben, in der weitere Eigenschaften, etwa von algebraischen Varietäten, berücksichtigt werden. Elliptische Kurven sind genau solche Objekte: sie sind einfache abelsche Varietäten der Dimension eins in der Kategorie der algebraischen Varietäten. Diese zusätzliche Einbettung sorgt für die nötige Struktur, die im Zusammenhang mit Diffie-Hellman den fundamentalen Unterschied macht – sie unterscheiden die privaten von den öffentlichen Schlüsseln auf eine Weise, die bei abstrakten Gruppen so nicht möglich ist.
Eine wichtige Erkenntnis daraus ist, dass das klassische Diffie-Hellman im klassischen Sinn eigentlich gar nicht existiert, wenn man das Problem rein gruppentheoretisch betrachtet. Es ist vielmehr ein Spezialfall des komplexeren elliptischen Kurvendiskreten-Logarithmusproblems im Kontext von algebraischen Gruppen. Auf diese Weise rücken elliptische Kurven ins Zentrum der Betrachtung und gewinnen im Vergleich zu anderen Gruppenführern ihre herausragende Stellung. Zusätzlich ist bemerkenswert, dass auch die bisher als traditionelle Alternative betrachtete multiplikative Gruppe der Einheiten eines endlichen Körpers – die Grundlage des klassischen Diffie-Hellman – als ein spezieller Grenzfall einer algebraischen Kurve verstanden werden kann. Im algebraischen Bereich begegnet man sogenannten singulären Kurven, und eine dieser Randformen verhält sich genau wie diese multiplikative Gruppe.
Somit ist auch das klassische finite field Diffie-Hellman streng genommen eine Variante vom elliptischen Kurvendiffie-Hellman, nur eben über eine „verzerrte“ oder singularisierte Kurve. Diese tiefgehende mathematische Einordnung ermöglicht es, die verschiedenen Methoden zur Schlüsselerzeugung und sicheren Kommunikation in einem einheitlichen Rahmen zu sehen und besser zu verstehen. Die Praxis hat diese Erkenntnisse bereits weit vor der theoretischen Vollständigkeit berücksichtigt. Insbesondere bei modernen Protokollen und in der Anwendung von TLS, VPNs und anderen sicherheitsrelevanten Anwendungen dominieren elliptische Kurven als Standard. Der Grund dafür ist nicht nur Effizienz, sondern eben auch die theoretische Fundierung, die sie zur einzig wirklich sinnvollen Gruppe im Kontext modernes Diffie-Hellman macht.
Der Weg von der abstrakten Algebra zur praktischen Sicherheit ist dabei bemerkenswert. Was anfänglich wie ein kryptisches mathematisches Detail erscheint, entfaltet sich zu einem grundlegenden Baustein der sicheren Kommunikation im Internet. Ohne die Verknüpfung von Gruppentheorie, algebraischer Geometrie und Kategorien wäre es kaum verständlich oder nachvollziehbar, warum gerade elliptische Kurven verwendet werden. Doch nicht nur die Mathematik leistet ihren Beitrag. Die Implementierung von elliptischen Kurven in Hardware und Software ermöglicht schnelle und gleichzeitig sichere Transaktionen, von der mobilen Endgerätverschlüsselung bis hin zu großen Cloud-Diensten.
Die kryptographischen Algorithmen sind durch diese Struktur weniger anfällig für Seitenkanalangriffe und können durch optimierte arithmetische Operationen auf elliptischen Kurven ressourcenschonend ausgeführt werden. Zukunftssicher sind elliptische Kurven außerdem insofern, dass neue mathematische Methoden sie bisher nicht leichter angreifbar machen konnten. Im Gegensatz zu den klassischen Verfahren auf großen Primzahlen wird das diskrete Logarithmusproblem auf elliptischen Kurven mit den heutigen und wahrscheinlich kommenden Algorithmen nicht effizient lösbar. Allerdings bleiben Forschende wachsam, da Quantencomputer theoretisch in der Lage wären, solche Probleme zu lösen, was die Suche nach Post-Quanten-Kryptographie vorantreibt. Trotzdem haben elliptische Kurven bis heute Maßstäbe gesetzt und die Art geprägt, wie digitale Sicherheit in der Praxis organisiert wird.
Ihr Einsatz erweitert sich auch zunehmend in neuen Anwendungen, wie Blockchain-Technologien, digitale Signaturen und Identitätsmanagementsysteme, was ihre Wichtigkeit zusätzlich unterstreicht. Zusammenfassend lässt sich sagen, dass elliptische Kurven nicht nur der beste praktische Kompromiss aus Sicherheit und Effizienz sind, sondern auch mathematisch die einzig wirklich sinnvolle Grundlage für Diffie-Hellman-ähnliche Schlüsselaustauschverfahren darstellen. Die Idee, einfach irgendeine Gruppe für Diffie-Hellman zu verwenden, funktioniert nicht ohne die weitere, tiefgehende Struktur, die elliptische Kurven bieten. Das macht das „klassische“ Diffie-Hellman eigentlich nur zu einem Spezialfall oder einer Randerscheinung im großen Zusammenhang moderner algebraischer Kryptographie. So zeigt sich, dass die Wahl von Elliptic Curve Diffie-Hellman keine bloße Modeerscheinung oder Marketing-Entscheidung ist, sondern das Ergebnis einer langwierigen, faszinierenden mathematischen Entwicklung, die Sicherheit und Effizienz auf höchstem Niveau miteinander verbindet.
Wer sich also für moderne Kryptographie interessiert, landet unausweichlich bei elliptischen Kurven, denn außer ihnen gibt es schlichtweg keine andere vernünftige Wahl, wenn es um Diffie-Hellman geht. Die Zukunft der sicheren Schlüsselvereinbarung bleibt somit klar mit elliptischen Kurven verbunden.