In der Welt der künstlichen Intelligenz und des maschinellen Lernens sind Multi-Layer-Perceptrons (MLPs) eine essentielle Komponente vieler neuronaler Netzwerke, darunter auch in den heute dominierenden Transformer-Architekturen. Trotz ihrer Bedeutung stellt das Verständnis ihrer inneren Funktionsweise nach wie vor eine Herausforderung dar. Traditionelle Interpretationsmethoden konzentrieren sich meist auf die Analyse von Aktivierungen, also wie das Modell auf spezifische Eingaben reagiert. Doch oftmals bleibt dabei unklar, wie genau die Gewichte in einem MLP dazu beitragen, dass bestimmte Merkmale erkannt und verarbeitet werden. Hier setzen bilineare MLPs an und bieten eine völlig neue Perspektive für die mechanistische Interpretierbarkeit von neuronalen Netzen durch eine direkte Analyse der Gewichte.
Der Hauptunterschied eines bilinearen MLP gegenüber klassischen Modellen besteht darin, dass er auf den Einsatz elementweiser Nichtlinearitäten verzichtet, wie sie in den meisten neuronalen Netzwerken üblich sind. Stattdessen nutzt ein bilinearer Aufbau eine spezielle Form von gekoppelten linearen Operationen, ähnlich einer Klasse von sogenannten Gated Linear Units (GLUs). Diese Umstellung ermöglicht eine mathematisch transparente Darstellung des MLPs mittels eines dritten Ordnungstensors, der das Netzwerkgewicht in einer strukturierten Form kodiert und so analysierbar macht. Die Abwesenheit von nichtlinearen Aktivierungsfunktionen schafft Raum für eine genauere Untersuchung der Gewichte direkt. Dadurch entfällt das komplexe Problem höherordentlicher Interaktionen, das in traditionellen MLPs mit Nichtlinearitäten häufig einen Blackbox-Effekt erzeugt.
Anhand linearer Algebra und Tensorzerlegungen kann man das Gewichtsmuster in bilinearen MLPs auseinandernehmen, was nicht nur eine bessere Visualisierung der wichtigsten Merkmale ermöglicht, sondern auch Einblicke in das zugrundeliegende Funktionsprinzip des Modells gibt. Wissenschaftler analysieren hierfür eigens entwickelte eigenspektrale Methoden. Mithilfe der Zerlegung der Gewichte in Eigenvektoren und Eigenwerte lässt sich der Einfluss unterschiedlicher gewichteter Komponenten auf die Modellleistung untersuchen. Es zeigt sich, dass die Modelle oft eine niedrigrangige Strukur besitzen, das heißt, sie projizieren Eingaben auf wenige dominierende Merkmale oder „Atome“. Diese vereinfachte Sichtweise hilft dabei, komplexe neuronale Netzwerke zu entwirren und nachvollziehbar zu machen.
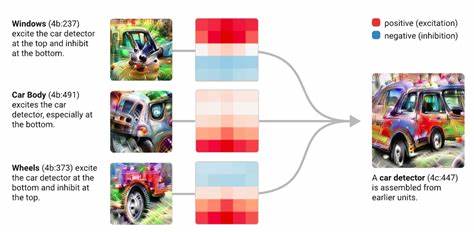
Die praktische Anwendung solcher Zugänge ist vielfältig. Im Bereich der Bildklassifikation konnten Forscher bilineare MLPs nutzen, um die Erkennung visueller Merkmale durch das Modell exakt zuzuordnen. So lässt sich nachvollziehen, welche Merkmalskombinationen oder Filter im Netzwerk besonders wichtig sind. Auch in der Sprachverarbeitung werden durch die Gewichtsanalyse spezifische Wechselwirkungen zwischen Sprachmerkmalen sichtbar, die bislang nur schwer zugänglich waren. Gerade bei kleineren Sprachmodellen zeigte sich, dass man sogenannte Feature-Circuits, also funktionale Rechenschaltungen im Modell, isolieren kann, indem man direkt die Gewichte untersucht, ohne auf Aktivierungswerte oder externe Tests zurückgreifen zu müssen.
Ein weiterer Vorteil bilinearer MLPs liegt in der Möglichkeit, gezielt adversariale Beispiele zu konstruieren. Diese gezielten Manipulationen von Eingaben zeigen auf, wie das Modell auf spezifische Muster sensitiv reagiert. Mit diesem Wissen lassen sich Schwachstellen und Überanpassungen (Overfitting) erkennen und somit gezielter regulieren oder korrigieren. Damit leisten bilineare MLPs nicht nur einen Beitrag zu besser interpretierbaren Modellen, sondern auch zur Qualitätskontrolle und Robustheit von KI-Systemen. Die Bedeutung dieses Ansatzes erstreckt sich über reine Forschungsinteressen hinaus.
In der Praxis sind bilineare Schichten leicht als Drop-in-Ersatz für herkömmliche Aktivierungsschichten einsetzbar. Dadurch bieten sie eine unkomplizierte Methode, tiefere Einblicke in Modelle zu gewinnen, ohne die Leistung zu opfern. Unternehmen und Entwickler, die absorbierbare und nachvollziehbare künstliche Intelligenzsysteme anstreben, können von bilinearen MLP-Strukturen stark profitieren. Neben den mechanistischen Vorteilen helfen bilineare Ansätze auch bei regulierenden Maßnahmen wie Gewichtstrunkierung, Gewichtszerlegung oder sparsamen Modellen. Die klare Darstellung der Gewichtsmatrix ermöglicht es, durch gezielte Regularisierung die Modellkomplexität zu steuern und die Generalisierung zu verbessern.
In Kombination mit bekannten Techniken wie gewichtsbasiertem Training oder Eingaberauschen tragen bilineare MLPs somit zu stabileren und effizienteren Netzwerken bei. Zudem erweitern bilineare Verfahren die Toolpalette der Interpretierbarkeit deutlich. Während klassische Aktivierungsbasierte Methoden oft nur beschreiben, welche Merkmale die Modelle erkennen, zeigen bilineare Modelle direkt, wie genau diese Merkmale aus den Gewichten zusammengesetzt werden. Durch moderne Tensorzerlegungstechniken lassen sich Muster aufdecken, die sonst verborgen bleiben. So entsteht eine tiefere mechanistische Sichtweise, die für grundlegendes Verständnis und Weiterentwicklung von KI-Technologien essenziell ist.
Die Zukunft der mechanistischen Interpretierbarkeit wird durch bilineare MLPs entscheidend mitgeprägt. Sie ermöglichen nicht nur eine griffigere Forschungsbasis, sondern auch praktische Anwendungen in Bereichen von der Bildverarbeitung über Sprachmodelle bis hin zu allgemeinen KI-Systemen. Mit zunehmender Verbreitung solcher Modelle wächst die Möglichkeit, künstliche Intelligenz transparent, nachvollziehbar und vertrauenswürdig zu gestalten. Abschließend zeigt sich, dass bilineare MLPs einen entscheidenden Schritt in Richtung besserer Verständnis und Steuerbarkeit komplexer neuronaler Modelle darstellen. Die Möglichkeit, direkte Einsicht in die Zusammensetzung von Gewichten und deren Wirkung zu erhalten, macht sie zu einem unverzichtbaren Werkzeug der modernen KI-Forschung und -Anwendung.
Für alle, die sich mit den inneren Mechanismen neuronaler Netzwerke beschäftigen, bieten bilineare MLPs eine vielversprechende und praktikable Lösung, um den Blackbox-Charakter der Modelle aufzubrechen und echte Erklärbarkeit zu schaffen.