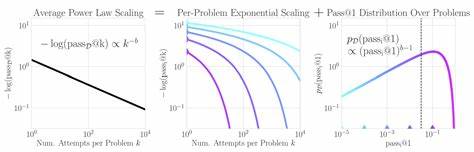
Sprachmodelle, besonders die großen multimodalen Varianten, revolutionieren die Welt der künstlichen Intelligenz. Sie helfen dabei, komplexe Probleme zu lösen, unterstützen bei der Programmierung von Beweisassistenten und überwinden sogar multimodale Barrieren, um vielseitige Aufgaben erfolgreicher zu meistern. Doch eine faszinierende Frage steht im Raum: Wie kommen diese Modelle zu ihrer beeindruckenden Leistungsfähigkeit? Die Antwort liegt in sogenannten Skalierungsgesetzen, die das Verhalten der Modelle in Abhängigkeit von Rechenressourcen und Versuchszahlen mathematisch beschreiben. Jüngste Forschungen verdeutlichen, dass bei dem Versuch, eine Reihe von Aufgaben mehrfach zu bewältigen, die negative Logarithmusfunktion der durchschnittlichen Erfolgsrate im Verhältnis zu den Versuchen einer Potenzgesetz-Skalierung folgt. Anders ausgedrückt: Wenn ein Sprachmodell dieselbe Aufgabe mehrfach versucht, fällt die Fehlerrate nicht einfach nur exponentiell ab, sondern auf aggregierter Ebene zeigt sie ein polynomiales Verhalten.
Dieses Skalierungsphänomen wirft zunächst ein Rätsel auf, denn die intuitive und einfache mathematische Erwartung lautet, dass die Fehlerwahrscheinlichkeit mit jedem neuen Versuch exponentiell sinken müsste. Das Kernproblem liegt darin, wie Erfolge und Misserfolge über viele Aufgaben hinweg gemittelt werden. Tatsächlich zeigt sich, dass die Erfolgswahrscheinlichkeiten für einzelne Aufgaben einer schweren Verteilung folgen, was bedeutet, dass ein kleiner Teil der Aufgaben extrem schwierig ist und eine sehr niedrige Erfolgswahrscheinlichkeit besitzt. Diese sogenannten "heavy-tailed" Verteilungen wirken sich stark auf das Gesamtergebnis aus und lassen das statistische Bild auf der aggregierten Ebene von einer exponentiellen zu einer polynomiellen Skalierung übergehen. Das Verständnis dieser Verteilung ist mehr als nur eine theoretische Spielerei.
Es hat direkte Auswirkungen darauf, wie wir die Leistung von Sprachmodellen bewerten und vorhersagen können. Die Forscher konnten zeigen, dass eine präzise Modellierung der Verteilung der Einzelerfolgswahrscheinlichkeiten es ermöglicht, die Exponenten des Potenzgesetzes deutlich genauer vorherzusagen. Das bedeutet konkret eine signifikante Reduktion des Rechenaufwands für Inferenzoperationen um mehrere Größenordnungen, da Vorhersagen mit weitaus weniger Versuchen möglich sind. Im Kontext moderner KI-Forschung ist diese Erkenntnis besonders wertvoll. Die immer größer werdenden Modelle erfordern stets steigende Rechenressourcen, und das Verständnis der zugrundeliegenden mathematischen Gesetze gibt Entwicklern ein Werkzeug an die Hand, um effizienter zu skalieren und vorherzusagen, wann ein System eine gewünschte Performance erreicht.
So können teure und zeitaufwändige Tests deutlich reduziert werden, was wiederum die technologische Entwicklung beschleunigt. Multimodale Modelle, die neben Text auch visuelle und andere Datentypen verarbeiten, profitieren besonders von diesem Wissen. Die Vielzahl an unterschiedlichen Aufgaben, auf die sie angewandt werden, bringt eine Bandbreite an Erfolgswahrscheinlichkeiten mit sich. Die Verteilung dieser Wahrscheinlichkeiten ist entscheidend dafür, wie gut das Modell im Gesamtdurchschnitt abschneidet. Ein tieferes Verständnis dieser Verteilung und der daraus resultierenden Skalierungsgesetze hilft Forschern dabei, die Architektur und das Training zukünftiger Modelle gezielter zu verbessern.
Neben dem offensichtlichen Nutzen für die Wissenschaft zeigt diese Forschungsarbeit auch interessante Parallelen zu anderen Bereichen der Statistik und Wahrscheinlichkeitstheorie. Beispielsweise lassen sich die Effekte schwerer Verteilungen in Finanzmärkten, Naturphänomenen und sozialen Netzwerken ähnlich beobachten. Dies verdeutlicht, wie verschiedenste komplexe Systeme durch einfache mathematische Prinzipien miteinander verbunden sind. In praktischen Anwendungen bedeutet das Verständnis der Skalierungsgesetze auch eine bessere Gestaltung von Systemen, die auf Sprachmodellen basieren, wie etwa automatische Übersetzungen, intelligente Assistenten oder dialogbasierte Systeme. Durch eine klügere Allokation von Rechenressourcen und eine effizientere Fehlerreduzierung steigt die Zuverlässigkeit solcher Systeme, was wiederum die Nutzererfahrung deutlich verbessert.
Zusammenfassend lässt sich sagen, dass die Leistungsfähigkeit großer Sprachmodelle nicht nur in ihrer Größe und Komplexität begründet liegt, sondern wesentlich durch die zugrunde liegenden mathematischen Skalierungsgesetze determiniert ist. Die Kombination aus exponentiellen Verbesserungen auf der Einzelaufgabenebene und einer aggregierten Potenzgesetz-Skalierung erklärt das bemerkenswerte Leistungswachstum sichtbar besser als frühere Modelle. Die Erforschung dieser Zusammenhänge repräsentiert einen bedeutenden Schritt für die KI-Forschung, der dabei hilft, sowohl theoretische Erkenntnisse als auch praktische Anwendungen voranzutreiben. Zukünftige Arbeiten, die auf diesen Erkenntnissen aufbauen, könnten neue Methoden entwickeln, um Sprachmodelle noch effizienter und leistungsfähiger zu machen – ein spannender Ausblick für die gesamte Branche rund um künstliche Intelligenz und maschinelles Lernen.