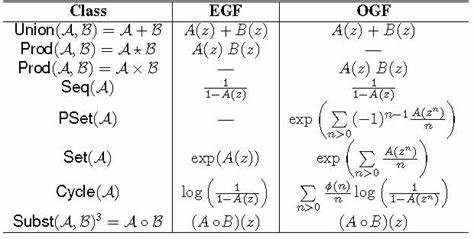
In der heutigen modernen Mathematik und theoretischen Informatik spielen algebraische Datentypen, kombinatorische Strukturen und erzeugende Funktionen eine zentrale Rolle. Diese drei Konzepte sind eng miteinander verknüpft und bilden die Grundlage für zahlreiche Anwendungen, von der Programmierung über die Kombinatorik bis hin zur komplexen Analyse von Algorithmen. Ein fundiertes Verständnis dieser Themen eröffnet Möglichkeiten, sowohl theoretische Modelle besser zu verstehen als auch praktische Probleme effizient zu lösen. Algebraische Datentypen stammen ursprünglich aus der Informatik, genauer gesagt aus der funktionalen Programmierung, wo sie als grundlegendes Konzept für die Definition von Datenstrukturen gelten. Sie ermöglichen es Programmierern, komplexe Datenmodelle auf elegante und typensichere Weise zu konstruieren.
Im Kern sind algebraische Datentypen kombinatorische Konstruktionen von Daten, die entweder als Summe (Disjunktion) oder Produkt (Konjunktion) von Typen dargestellt werden können. Dies erlaubt beispielsweise die Definition von Baumstrukturen, Optionstypen oder auch benutzerdefinierten Datentypen, die die Grundlage für rekursive Datenmodelle bilden. Auf der anderen Seite ist die Kombinatorik das mathematische Fachgebiet, das sich mit der Anordnung, Zusammenstellung und Auswahl von Objekten beschäftigt. Kombinatorische Strukturen wie Graphen, Permutationen, Partitionen und Bäume sind in vielen Bereichen von großer Bedeutung. Sie sind nicht nur Gegenstand theoretischer Untersuchungen, sondern finden auch praktische Anwendung in Bereichen wie der Algorithmik, Optimierung und Statistik.
Die Verbindung zwischen algebraischen Datentypen und kombinatorischen Strukturen zeigt sich vor allem darin, dass viele Datentypen durch kombinatorische Modelle beschrieben und analysiert werden können. Dabei helfen algebraische Definitionen, komplexe Strukturen systematisch zu erfassen und zu manipulieren. Ein weiteres fundamentales Werkzeug in diesem Kontext sind erzeugende Funktionen. Diese mathematischen Funktionen verknüpfen kombinatorische Objekte mit Potenzreihen und ermöglichen somit die einfache Analyse und Enumeration großer Strukturen. Durch die Verwendung von erzeugenden Funktionen lassen sich zum Beispiel Anzahlen von Objekten mit bestimmten Eigenschaften effizient berechnen oder asymptotische Verteilungen bestimmen.
In der Mathematik und Informatik sind solche Techniken unverzichtbar, besonders wenn es gilt, komplexe Probleme zu lösen, die mit Themen wie der Analyse von Algorithmen, Probabilistik oder formalen Sprachen zusammenhängen. Das Zusammenspiel von algebraischen Datentypen, kombinatorischen Strukturen und erzeugenden Funktionen lässt sich anhand zahlreicher Beispiele illustrieren. Betrachten wir etwa die binären Bäume, die eine Schlüsselrolle in vielen Datenstrukturen und Algorithmen einnehmen. Diese Bäume können als ein algebraischer Datentyp definiert werden, der rekursiv entweder leer ist oder einen Knoten mit zwei Unterbäumen enthält. Die zugehörige kombinatorische Struktur erlaubt es, die Anzahl aller binären Bäume mit einer bestimmten Knotenanzahl zu bestimmen, wozu erzeugende Funktionen genutzt werden.
Die Catalan-Zahlen, die in diesem Zusammenhang eine wichtige Rolle spielen, können elegant durch die erzeugende Funktion der binären Bäume dargestellt und berechnet werden. Ein weiteres Beispiel sind Listenstrukturen. Listen können algebraisch als entweder leer oder als ein Kopf-Element gefolgt von einer weiteren Liste modelliert werden. Diese einfache, aber mächtige Definition ist eng verwandt mit der Kombinatorik der Folgen und Permutationen. Die erzeugende Funktion für Listen ist eine fundamentale Konzept, das sich leicht ableiten lässt und vielseitige Anwendung in der Informatik findet, etwa bei der Analyse von Algorithmen zur Sortierung oder Suche.
Neben der Anwendung in der Theorie haben diese Konzepte auch praktische Relevanz in der Softwareentwicklung. Algebraische Datentypen erlauben eine präzise Modellierung von Programmdaten, was die Lesbarkeit, Wartbarkeit und Fehlersicherheit von Code verbessert. Funktionale Programmiersprachen wie Haskell oder Scala nutzen diese Datentypen intensiv. Kombinatorische Strukturen wiederum helfen bei der Entwicklung von Algorithmen, indem sie die Basis für effiziente Datenmodelle und Datenmanipulation bilden. Erzeugende Funktionen unterstützen Entwickler und Mathematiker, um die Komplexität von Prozessen zu analysieren und Vorhersagen über das Verhalten von Systemen zu treffen.
Ein oft zitiertes Gebiet, in dem all diese Konzepte zusammenfließen, ist die Analyse von Algorithmen, insbesondere im Bereich der durchschnittlichen Laufzeit und der Wahrscheinlichkeitsverteilung von Ergebnissen. Hier erlaubt die Verwendung algebraischer Datentypen eine formale Darstellung der Eingabestrukturen, während kombinatorische Methoden deren Eigenschaften untersuchen. Erzeugende Funktionen liefern dann leistungsfähige Werkzeuge zur Quantifizierung und asymptotischen Analyse. Darüber hinaus bieten algebraische Datentypen, kombiniert mit erzeugenden Funktionen, effiziente Mittel zur automatischen Berechnung von Gleichungen und Identitäten in der Kombinatorik. Diese Möglichkeiten werden durch moderne Computeralgebrasysteme unterstützt, die es erlauben, komplexe Berechnungen und Beweise auf sichere Art und Weise durchzuführen.
So können auch sehr komplizierte kombinatorische Probleme algorithmisch angegangen werden. Es lohnt sich auch, den historischen Hintergrund zu betrachten. Die Grundlagen der algebraischen Datentypen wurden maßgeblich durch die Entwicklung der Typentheorie und der Lambda-Kalküle geprägt, während die Kombinatorik eine lange Tradition in der Mathematik hat, verteilt auf Bereiche wie Zahlentheorie und Geometrie. Die Theorie der erzeugenden Funktionen wurde im 18. und 19.
Jahrhundert entwickelt und hat sich seither als elementares Werkzeug etabliert. Die heutige Synthese dieser Disziplinen spiegelt den interdisziplinären Charakter moderner Wissenschaft wider. Neben theoretischen Aspekten geht es auch um die kognitive Komponente: Die Wahl bestimmter algebraischer Datentypen und die Nutzung erzeugender Funktionen fördern ein besseres Verständnis der zugrundeliegenden Strukturen. Sie liefern eine gemeinsame Sprache für Mathematiker und Informatiker, um komplexe Probleme zu beschreiben und zu lösen. Dies verdeutlicht, wie abstrakte Theorien auf konkrete Probleme Einfluss nehmen und zum Fortschritt der Wissenschaft beitragen.
Nicht zuletzt eröffnen laufende Forschungen im Bereich algebraischer Datentypen, kombinatorischer Strukturen und erzeugender Funktionen spannende Perspektiven für die Zukunft. Die Kombination dieser Konzepte findet zunehmend Anwendung in neuen Disziplinen wie dem maschinellen Lernen, der Bioinformatik oder der Quanteninformatik. Hier werden Datenmodelle und Strukturuntersuchungen auf ganz neue Weise genutzt, was zu innovativen Lösungen und einem besseren Verständnis komplexer Systeme führt. Zusammenfassend ist klar, dass algebraische Datentypen, kombinatorische Strukturen und erzeugende Funktionen unverzichtbare Werkzeuge im Arsenal von Mathematikern und Informatikern sind. Durch ihr starkes Zusammenspiel ermöglichen sie eine effiziente Beschreibung, Analyse und Lösung vielfältiger Probleme.
Das Bewusstsein für ihre Bedeutung und die Fähigkeit, sie gezielt einzusetzen, ist für alle, die sich mit theoretischer oder angewandter Mathematik und Informatik befassen, von großem Vorteil.