Die Berechnung der transitiven Hülle eines Graphen zählt zu den klassischen Problemen in der Graphentheorie und Informatik. Dabei geht es darum, für einen gegebenen gerichteten Graphen alle erreichbaren Knoten von jedem einzelnen Knoten aus zu bestimmen. Die transitive Hülle erweitert somit die ursprüngliche Erreichbarkeitsbeziehung, indem indirekte Verbindungen ebenfalls erfasst werden. Insbesondere bei kleinen Graphen mit höchstens acht Knoten eröffnet die Verwendung spezieller Repräsentationen und Optimierungen wie Bitmathematik und SIMD (Single Instruction, Multiple Data) neue Wege für eine hochperformante Umsetzung. Grundlage bildet häufig die Warshall-Variante des Floyd-Warshall-Algorithmus, der statt kürzester Wege die transitive Hülle mittels boolescher Matrizen berechnet.
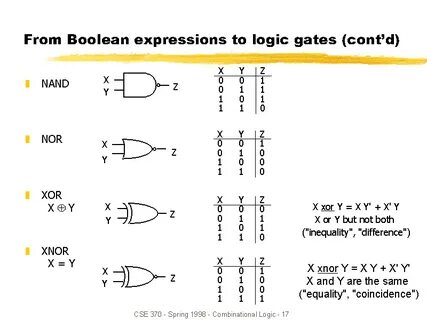
Stellvertretend wird ein Graph als 8x8-Matrix mit Booleschen Werten dargestellt, wobei jeder Eintrag angibt, ob eine direkte Kante zwischen zwei Knoten existiert. Die direkte Umsetzung des Algorithmus arbeitet hierbei auf einzelnen Bits und prüft – entsprechend der Logik – für jedes Tripel von Indizes (i, j, k), ob ein Weg von i über k nach j existiert, und setzt gegebenenfalls den Eintrag. Diese klassische Implementierung über std::bitset oder einzelne boolesche Werte ist auf den ersten Blick einfach und nachvollziehbar, birgt aber erhebliche Performanceengpässe durch die sequenzielle Verarbeitung einzelner Bits. Gerade bei moderner Hardware bieten sich Möglichkeiten, solche Operationen gleichzeitig auf mehreren Bits — je nach Bitbreite eines Datentyps bis zu 64 Bits parallel — auszuführen, was immens beschleunigen kann. Ein entscheidender Schritt ist also, die graphische Relation als 64-Bit-Wert zu repräsentieren, wobei jede Bitposition einer Kante in der Matrix entspricht.
Das erlaubt einen direkten Zugriff und Manipulation mit bitweisen Operatoren, die in CPU-Registern sehr effizient auszuführen sind. Dabei wird die Verknüpfung zwischen Zeilen und Spalten des Graphen in Form von Bitmasken genutzt, um parallele Aktualisierungen zu ermöglichen. Eine elegant optimierte Variante des Warshall-Algorithmus nutzt die Tatsache, dass die k-te Zeile der Matrix isoliert betrachtet und für alle Zeilen i, bei denen ein direkter Zugang zum Knoten k besteht, in die i-te Zeile mittels einer bitweisen OR-Operation eingefügt werden kann. Diese Vereinfachung reduziert den Algorithmus auf grundlegende Bitshifts, Maskierungen und Multiplikationen – Operationen, die insbesondere auf CPUs extrem schnell sind. Der nächste Entwicklungsschritt führt zu einer Implementierung, bei der nicht nur einzelne Bits geprüft werden, sondern sowohl die zu prüfende Bedingung als auch die anzuwendende Operation in Form von Bitmasken vorliegen.
Die Nutzung eines Multiplikations-Tricks sorgt für parallele Verteilung des k-ten Zeilenbits auf die relevanten Zeilen. Zusammen mit einer OR-Verknüpfung werden so alle nötigen Aktualisierungen effizient umgesetzt. Diese technische Finesse trägt dem Umstand Rechnung, dass sich die ursprünglichen if-Bedingungen durch reine Bitoperationen ersetzen lassen. Im Ergebnis werden pro Iteration des Algorithmus alle notwendigen Modifikationen an der transitive Hülle in teilweise parallelisierter Form ausgeführt, was deutliche Zeitgewinne gegenüber einer naive for-Schleifen-Implementierung realisiert. Weitere Performancegewinne können durch den Einsatz von SIMD-Instruktionen erzielt werden, die es erlauben, parallele Datenströme simultan zu verarbeiten.
AVX2 oder AVX-512 SIMD-Erweiterungen moderner x86-Prozessoren ermöglichen, mehrere Graphen gleichzeitig in Vektorregistern zu laden und mit den genannten bitweisen Operationen parallel zu bearbeiten. Somit wird nicht nur der Algorithmus für einen einzelnen Graphen optimiert, sondern durch Batch-Verarbeitung signifikant die Gesamtdurchsatzrate erhöht. Mit Hilfe spezieller Instruktionen wie _mm256_shuffle_epi8 oder _mm256_blendv_epi8 lassen sich gezielt Bitpermutionen oder Maskierungsoperationen durchführen, die für die Umsetzung der transitive Hülle notwendig sind. Auch die Anwendung von Multiplikationen auf Vektorebene zur Verteilung von Bits auf die korrekten Positionen kann so realisiert werden. Dabei wird der SIMD-Ansatz mit einer Unroll-Strategie kombiniert, welche die Loop-Overhead reduziert und die Instruktionsausführung optimiert.
Der Aufruf von SIMD-Funktionen im Rahmen der transitive-Hülle-Berechnung ist hierbei nicht nur ein reines Geschwindigkeitstool, sondern ermöglicht auf moderner Hardware auch Energieeffizienzsteigerungen, da weniger CPU-Zyklen verbraucht werden und besserer Durchsatz erzielt wird. Besonders in Anwendungen, wo Vielzahl kleiner Graphen zu bearbeiten sind, wie in Netzwerk- oder Datenbankanalysen, ergeben sich so direkte praktische Vorteile. Neben rein CPU-seitigen Optimierungen wird in der Community immer wieder über mögliche hardwarebeschleunigte Implementierungen wie spezielle Matrix-Operationseinheiten oder Instruktionen wie MOR (Matrix OR) diskutiert. MOR ist eine spezielle binäre Matrixmultiplikation, die OR- und AND-Operationen benutzt und der Floyd-Warshall-Transitive-Hülle-Rechnung formal nahekommt. Obwohl sie theoretisch sehr elegant ist, zeigen praktische Messungen, dass handoptimierte bitweise Algorithmen oft schneller oder zumindest kompetitiv sind, da sie direkt auf bestehende CPU-Registerarchitekturen zugeschnitten sind.
Insgesamt lässt sich festhalten, dass die Kombination aus boolescher Graphrepräsentation, Bitmathematik und Nutzung moderner SIMD-Technologie hochgradig effiziente Berechnung der transitiven Hülle bei kleinen Graphen ermöglicht. Die praktische Bedeutung liegt dabei nicht nur in der algorithmischen Eleganz, sondern vor allem in greifbaren Geschwindigkeitsvorteilen, die in datenintensiven Systemen von hohem Wert sind. Darüber hinaus eröffnet der Fokus auf kleine Graphen neue Anwendungsperspektiven, bei denen komprimierte Bitmatrizen und parallelisierte Verarbeitung neue Analysefreiräume schaffen. Von Graphen in der Netzwerkanalyse über Pattern Matching bis zu formalen Verifikationsprozessen und KI-Algorithmen – das effiziente Handling der transitiven Hülle ist Grundvoraussetzung für viele weiterführende Verfahren. Gerade der bewusste Verzicht auf unkomprimierte Datenstrukturen und der Einsatz spezialisierter Bit- und SIMD-Techniken zeigen, dass sich traditionelle Probleme der Graphentheorie mit modernster Hardware nah am Metall immer weiter optimieren lassen.
Zu verstehen, wie man logische Operationen geschickt in mathematische Bitoperationen übersetzt und diese mit Vektoroperationen verbindet, bildet somit eine essenzielle Kompetenz moderner Softwareentwicklung für hochperformante graphbasierte Algorithmen. Ein besonderer Aspekt ist außerdem die Portabilität und Skalierbarkeit der vorgestellten Methoden. Während hier am Beispiel von 8x8-Matrizen erläutert wurde, lassen sich ähnliche Grundprinzipien für größere Graphen mit mehr Knoten oder in parallelen Verarbeitungseinheiten umsetzen. Besonders durch geeignete Partitionierung und Chunking der Daten kann die zugrunde liegende Bitmathematik erweitert werden. Fazit: Die Berechnung der transitiven Hülle kleiner Graphen profitiert maßgeblich von der Verknüpfung klassischer boolescher Logik mit moderner Bitmathematik und SIMD-Optimierungen.
Die optimale Nutzung von CPU-Befehlssätzen, Bitmasken und paralleler Verarbeitung schafft schnelle und energieeffiziente Algorithmen, die vielfältige praktische Anwendungsmöglichkeiten bieten. Die Kombination aus algorithmischer Raffinesse und hardwareangepasster Implementierung stellt dabei einen idealen Weg dar, um auch komplexe graphentheoretische Probleme performant zu lösen und neue Effizienzstandards in der Informatik zu setzen.