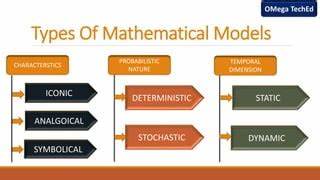
Mathematische Modelle bilden das Rückgrat zahlreicher wissenschaftlicher Disziplinen. Sie ermöglichen es, komplexe Phänomene zu analysieren, Hypothesen zu formulieren und empirische Beobachtungen in verständliche Zusammenhänge zu überführen. Doch nicht alle Modelle sind gleich – sie unterscheiden sich in ihrer Grundstruktur, ihrem Aufbau und ihrem Erkenntnisziel. Besonders hilfreich ist die Einteilung in drei Typen: Abstraktionen, Heuristiken und sogenannte In-silico-Modelle. Diese Kategorien geben nicht nur Aufschluss darüber, wie Modelle konstruiert und angewendet werden, sondern auch über die Art der Erkenntnisse, die sie liefern.
Abstraktionen als Fundament der theoretischen Forschung Abstrakte Modelle sind vor allem in der Mathematik und theoretischen Informatik zu finden. Sie dienen der präzisen Beschreibung von Konzepten, Theorien und Systemen in möglichst allgemeiner Form. Das Ziel ist es, universelle Aussagen über eine ganze Klasse von Modellen oder Systemen zu treffen und so Verallgemeinerungen zu ermöglichen. Abstraktionen sind durch ihre hohe Allgemeingültigkeit gekennzeichnet und helfen dabei, grundlegende Prinzipien zu verstehen, die ansonsten im Detail verlorengehen könnten. Ein typisches Beispiel für abstrakte Modelle sind Turingmaschinen, die eine theoretische Grundlage für Berechenbarkeit darstellen.
Durch sie lassen sich Limits der Berechenbarkeit und Probleme wie die Unentscheidbarkeit beweisen. Abstraktionen erleichtern es, komplexe Systeme durch aufeinander aufbauende logische Schlussfolgerungen zu durchdringen. Die Darstellung erfolgt meist analytisch oder algorithmisch, wobei die Aussagen streng formal und beweisbar sind. Heuristische Modelle und der kreative Umgang mit Komplexität Heuristiken wiederum zeichnen sich durch ein pragmatisches Vorgehen aus. Sie entstehen häufig dort, wo eine exakte Abbildung der Realität aufgrund von Komplexität, Unsicherheiten oder fehlenden Daten nicht möglich ist.
Heuristische Modelle arbeiten mit Vereinfachungen, Annahmen und manchmal sogar absichtlichen Unschärfen, um Modelle zu erzeugen, die trotz ihrer Fehler oder Ungenauigkeiten nützliche Einsichten liefern können. In den Sozial- und Biowissenschaften sind heuristische Modelle weit verbreitet. Sie erlauben Forscherinnen und Forschern, Hypothesen in formaler Sprache darzustellen, deren Konsequenzen zu überprüfen und so grundlegende Ideen zu testen. Die Annahmen dieser Modelle müssen nicht zwangsläufig empirisch beweisbar oder wahrheitsgetreu sein. Vielmehr dienen sie als geistige Werkzeuge, sogenannte „Fabeln“ oder Gedankenspiele, die zum besseren Verständnis oder zur Anregung neuer Forschungsfragen beitragen.
Die Präsentation heuristischer Modelle kann analytisch erfolgen, indem bestimmte Annahmen in mathematische Gleichungen überführt werden. Algorithmische Perspektiven können ebenfalls eine Rolle spielen, etwa wenn allgemeine Schritte in einem Prozess abstrahiert und als allgemeine Verfahren dargestellt werden. Außerdem sind computerbasierte Simulationen eine gängige Möglichkeit, mit heuristischen Modellen experimentell zu arbeiten. Hierbei ergeben sich jedoch Herausforderungen: Ohne strenge Verknüpfung von Annahmen und Ergebnissen bleiben diese Simulationen oft schwer interpretierbar und können mehr Verwirrung als Verständnis stiften. In-silico-Modelle: Computergestützte Abbilder der Realität Der Begriff In-silico stammt von der Analogie zu In-vivo und In-vitro und beschreibt mathematische Modelle, die auf Computern simuliert werden, um Prozesse in der realen Welt nachzubilden.
Sie sind besonders in den Physikwissenschaften und in der Ingenieurwissenschaft verbreitet, wo genaue Modelle auf empirisch messbaren Parametern basieren und Vorhersagen mit hoher Zuverlässigkeit treffen. In-silico-Modelle werden vor allem numerisch gelöst oder simuliert. Sie reproduzieren relevante Eigenschaften realer Systeme und ermöglichen Vorhersagen über deren zukünftigen Zustand. Typische Beispiele sind die Simulation von Himmelsmechanik bei Raumfahrtmissionen oder die Berechnung von mechanischen Belastungen in Bauwerken. In der Forschung dienen sie dazu, Theorien anhand von Daten zu überprüfen oder umgekehrt experimentelle Ergebnisse besser zu verstehen.
Der Anspruch von In-silico-Modellen ist ein enger Bezug zur Realität. Diskrepanzen zwischen Simulation und experimentellen Befunden führen oft zu einer kritischen Neubewertung der zugrunde liegenden Theorien. Deshalb sind In-silico-Modelle sowohl Werkzeuge der Vorhersage als auch der Theorieprüfung. Die drei Präsentationsformen von Modellen Neben der Art der Modelle unterscheidet sich auch ihre Präsentation in drei Formen: analytisch, algorithmisch und computational. Die analytische Präsentation ist geprägt von formalen, oft geschlossenen mathematischen Darstellungen, etwa durch Differentialgleichungen oder algebraische Systeme.
Sie ermöglicht es, Modelle schriftlich zu formulieren und mit bewährten Techniken Lösungen oder qualitative Aussagen abzuleiten. Algorithmische Präsentationen fokussieren auf Verfahren und Regeln, die von Computern ausgeführt werden können. Sie beschreiben Abläufe, nach denen aus gegebenen Bedingungen Lösungen oder Ergebnisse ermittelt werden können. Hier steht die Konstruktion von Algorithmen im Vordergrund, die universelle Eigenschaften des zu untersuchenden Systems erfassen. Computationale Präsentationen hingegen sind Simulations-basiert.
Sie setzen auf numerische Näherungslösungen, Monte-Carlo-Methoden oder Agentenbasierte Simulationen, um das Verhalten komplexer Systeme zu untersuchen. Sie sind oft der einzige Weg, wenn analytische oder algorithmische Beschreibungen nicht zugänglich oder zu rein theoretisch sind. Wechselwirkungen und Herausforderungen Die drei Modelltypen sind nicht strikt getrennt, sondern bilden ein Spektrum. Abstrakte Modelle liefern allgemein gültige Aussagen, die die Basis für heuristische Modelle sein können. Heuristische Modelle bringen oft kreative Hypothesen hervor, die wiederum in In-silico-Modelle integriert und überprüft werden können.
Doch gerade in den empirisch orientierten Sozial- und Biowissenschaften zeigt sich, dass die Balance zwischen Realitätsnähe und Anwendbarkeit eine große Herausforderung ist. Heurismen können zwar Einsichten bringen, sind aber anfällig für Fehlschlüsse, wenn man ihre Annahmen zu ernst nimmt. In-silico-Modelle sind oft sehr datenintensiv und erfordern ein gutes Verständnis der zugrunde liegenden Theorien, sonst droht eine blinde Abhängigkeit von Simulationsergebnissen ohne tieferes Verständnis. Zudem steht die Wissenschaftscommunity immer wieder vor der Aufgabe, Modelle so transparent und nachvollziehbar wie möglich zu gestalten, um Vertrauen in ihre Ergebnisse zu garantieren. Der stetige Austausch zwischen Theorie, Simulation und empirischer Überprüfung ist dabei entscheidend.