Die Zahl Pi ist eine der bedeutendsten Konstanten in der Mathematik, bekannt für ihre unendliche, nicht periodische Dezimalentwicklung und ihre fundamentale Rolle in Geometrie, Analysis und zahlreichen Anwendungsbereichen. Gleichzeitig ist Pascals Dreieck ein klassisches mathematisches Objekt, das auf den ersten Blick nichts mit Kreisen oder Pi zu tun haben scheint. Es ist eine wohlstrukturierte Anordnung binomialer Koeffizienten, die in vielen Bereichen wie Kombinatorik, Wahrscheinlichkeitsrechnung und Algebra Anwendung findet. Doch hinter dieser vermeintlichen Trennung verbirgt sich seit Jahrhunderten eine faszinierende Verbindung, die in den letzten Jahrzehnten immer wieder Forscher und Mathematikliebhaber inspiriert hat. Die Entdeckung von Pi in Pascals Dreieck überzeugt skeptische Gemüter, zeigt die Schönheit mathematischer Zusammenhänge und eröffnet neue Perspektiven für die Analyse von Reihen und binomialen Strukturen.
Ursprünge und Geschichte der Verbindung zwischen Pi und Pascal Schon in der Antike hat sich die Mathematik mit der Berechnung von Pi beschäftigt, wobei die frühesten Annäherungen durch Archimedes oder später Nilakantha Somayaji erarbeitet wurden. Nilakantha, ein indischer Mathematiker des 15. Jahrhunderts, entwickelte eine besonders elegante Reihe zur Annäherung von Pi, die heute noch als Nilakantha-Reihe bekannt ist. Diese Reihe beschreibt Pi als Summe einer alternierenden Reihe rationaler Brüche, deren Nenner Produkte dreier aufeinanderfolgender Zahlen sind. Interessanterweise haben moderne Forscher wie Daniel Hardisky diese klassische Reihe neu interpretiert und dabei eine überraschende Verbindung zu Pascals Dreieck hergestellt.
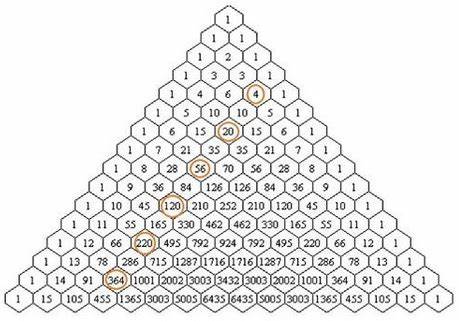
Hardisky stützte sich dabei auf Beobachtungen von Tony Foster, welcher herausfand, dass die Nenner der Nilakantha-Reihe als Flächen von Pythagoreischen Dreiecken interpretiert werden können. Da diese Dreiecke wiederum ganzzahlige Seitenlängen besitzen und durch bestimmte Parameter beschrieben werden, lässt sich ihr Flächeninhalt mit Produkten aufeinanderfolgender Zahlen darstellen – genau die Art von Zahlen, die auch in den Binomialkoeffizienten von Pascals Dreieck auftauchen. Mathematische Grundlagen: Binomialkoeffizienten und Pascals Dreieck Pascals Dreieck ist eine dreiecksförmige Anordnung von Zahlen, bei der jede Zahl die Summe der beiden Zahlen direkt darüber ist. Mathematisch entsprechen die Zahlen den Binomialkoeffizienten, die auch in der Binomialtheorie verwendet werden. Ein Binomialkoeffizient C(n, k) gibt an, auf wie viele Arten man k Elemente aus einer Menge von n Elementen auswählen kann.
Diese Koeffizienten treten nicht nur in Kombinatorik und Wahrscheinlichkeitsrechnung auf, sondern auch in Polynomausdrücken, wenn man Potenzen von Summen entwickelt. Die Verbindung zu Pi entsteht, wenn man unendliche Reihen betrachtet, die Pi approximieren, und deren Nenner beziehungsweise Summanden mit diesen Binomialkoeffizienten in Beziehung gesetzt werden können. Zum Beispiel kann die Leibniz-Reihe für Pi durch die Summe der Kehrwerte von bestimmten Binomialkoeffizienten ausgedrückt werden. Ebenso gibt es Umformungen der Nilakantha-Reihe, bei denen die Nenner explizit über Binomialkoeffizienten dargestellt werden – eine Beobachtung, die es erlaubt, Pi im Kontext von Pascals Dreieck zu sehen. Die Nilakantha-Reihe und ihre Modifikation Die Nilakantha-Reihe stellt Pi dar als 3 plus eine unendliche abwechselnde Reihe, in der Brüche mit Zählern 4 im Zähler und Nennern aus Produkten aufeinanderfolgender Zahlen auftauchen, zum Beispiel 4/(2·3·4) - 4/(4·5·6) + 4/(6·7·8) und so weiter.
Daniel Hardisky modifizierte diese Darstellung, indem er die Nenner der Terme als Binomialkoeffizienten umschrieb. Seine Version lautet 3 plus (2/3) mal eine Reihe, in der die Summanden Wechsel von Kehrwerten bestimmter Binomialkoeffizienten sind, nämlich C(4,3), C(6,3), C(8,3) und so weiter. Diese Umformung knüpft die Annäherung an Pi direkt an die Struktur von Pascals Dreieck an und hebt die Rolle der Binomialkoeffizienten hervor. Die Nenner sind dabei eng mit den Flächen von Pythagoreischen Dreiecken verbunden, die durch spezielle Werte parametrisiert sind. So erhält man eine geometrische Intuition hinter der Serie, die Pi definiert.
Pythagoreische Dreiecke als Schlüssel zur Verknüpfung Die Seiten eines pythagoreischen Dreiecks lassen sich durch Zahlen m und n mit der Bedingung m > n > 0 darstellen: a = 2mn, b = m² - n², c = m² + n². Die Fläche des Dreiecks ergibt sich als A = ab/2 = mn(m² - n²). Werden hier spezielle Werte für n genutzt, zum Beispiel n = 1, führt dies zu Produkten dreier aufeinanderfolgender Zahlen (m - 1) m (m + 1), die wie die Nenner in der Reihe für Pi erscheinen. Diese Beobachtung stellt den Zusammenhang zwischen Pythagoräischen Flächen, den Binomialkoeffizienten von Pascals Dreieck und der Approximierung von Pi her. Die Zahlen, die hier entstehen, sind eng mit der Binomialstruktur von Pascals Dreieck verbunden und erklären, warum sich Pi über diese Anordnung ausdrücken lässt.
Weitere Reihen für Pi und ihre binomialen Darstellungen Neben der Nilakantha-Reihe gibt es weitere Reihen, die Pi ungeachtet ihrer Herkunft mit Binomialkoeffizienten in Verbindung bringen. Zum Beispiel die Leibniz-Reihe, die Pi auf einfache Weise als alternierende Summe von Kehrwerten von ungeraden Zahlen darstellt, lässt sich auch als alternierende Summe von Kehrwerten bestimmter Binomialkoeffizienten repräsentieren. Konkret kann man schreiben, dass Pi/4 gleich einer alternierenden Reihe der Kehrwerte von C(3,1), C(5,1), C(7,1) und so weiter ist, was wiederum die Verknüpfung mit Pascals Dreieck verdeutlicht. Ebenso wurde von Jonas Castillo Toloza eine außergewöhnliche Reihe entdeckt, in der Pi minus 2 als eine Folge von Brüchen mit Zählern 1 und Nennern, die sich aus den Dreieckszahlen (Triangularzahlen) ergeben, dargestellt wird. Diese Reihe wechselt nach einem bestimmten Muster von Vorzeichen und verbindet erneut Pascals Dreieck, da auch Dreieckszahlen direkt mit Binomialkoeffizienten zusammenhängen, nämlich als C(n,2).
Diese Ergebnisse erweitern das Bild, wie vielfältig Pi in binomialen Strukturen verborgen sein kann. Bedeutung und Anwendungen der Entdeckungen Die Entdeckung solcher Verbindungen zwischen Pi und Pascals Dreieck ist nicht nur eine mathematische Kuriosität, sondern auch ein Spiegelbild der tiefen Vernetzung unterschiedlicher mathematischer Bereiche. Die Rekursivität von Pascals Dreieck, seine Verbindung zur Kombinatorik und die historischen Reihen für Pi werden auf unerwartete Weise miteinander verknüpft. Solche Erkenntnisse verstärken unser Verständnis von Zahlentheorie, Reihenentwicklungen und kombinatorischen Strukturen. Obwohl diese Reihen nicht unbedingt die effizientesten Methoden für die numerische Bestimmung von Pi darstellen, liefern sie wertvolle Einsichten in die Natur mathematischer Konstanten und deren Approximationen.