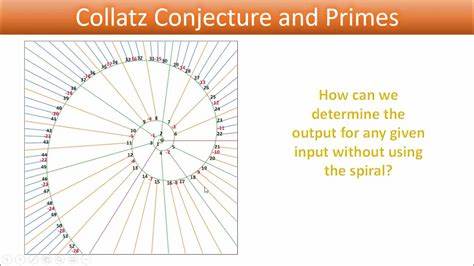
Die Collatz-Vermutung, auch unter Namen wie 3n+1-Verfahren bekannt, ist eines der bekanntesten ungelösten Probleme der Mathematik. Sie beschreibt eine Iteration über natürliche Zahlen, bei der jede ungerade Zahl mit 3 multipliziert und 1 addiert wird, während gerade Zahlen halbiert werden. Die Vermutung besagt, dass unabhängig von der Startzahl die Folge letztendlich immer bei der Zahl 1 endet. Obwohl diese Aussage extrem simpel erscheint, wurde sie bisher weder bewiesen noch widerlegt und fasziniert daher seit Jahrzehnten Forscher und Zahlenliebhaber. Die klassische Betrachtung der Collatz-Folge führt oft zu scheinbar chaotischen Zahlenreihen, deren Muster schwer zu durchdringen sind.
Eine moderne Herangehensweise zielt darauf ab, das zugrunde liegende Rauschen zu reduzieren, um die verborgenen Strukturen sichtbar zu machen. Genau an dieser Stelle spielen Primfaktorzerlegungen eine wichtige Rolle. Durch die sorgfältige Betrachtung der Primfaktoren bestimmter Zahlen in der Folge lassen sich charakteristische Muster aufdecken, die den Ablauf der Collatz-Iteration maßgeblich beeinflussen. Im Kern geht es dabei um die Analyse des sogenannten „Kontrollwertes“ bei jedem Schritt der Iteration. Für eine gegebene ungerade Zahl c betrachtet man die Zahl c+1, deren Primfaktorzerlegung Aufschluss darüber gibt, wie die Folge als nächstes verläuft.
Insbesondere sind die Faktoren 2 und 3 von zentraler Bedeutung, da sie in den Multiplikations- und Teilungsoperationen der Folge stark zum Tragen kommen. Die reduzierten Schritte des Collatz-Prozesses zeigen, dass durch die Optimierung, welche unnötige Iterationen eliminiert, jede ungerade Zahl c in einen Wert überführt wird, der sich durch Multiplikation mit 3 und anschließendes Teilen durch 2 charakterisieren lässt. Dieses Verfahren lässt sich weiter interpretieren, indem man die Anzahl der Zweien in der Primfaktorzerlegung von c+1 untersucht. Diese Anzahl bestimmt die Länge der sogenannten aufsteigenden Kette innerhalb der Folge. Die aufsteigende Kette beschreibt eine Folge von Werten, bei denen primär Faktoren von 2 schrittweise durch Faktoren von 3 ersetzt werden.
Dabei spiegelt die Anzahl der Zweien den Fortschritt innerhalb dieser Kette wider: Je mehr Zweien vorhanden sind, desto weiter am Beginn der Kette steht der Wert, während eine verringerte Anzahl auf einen fortgeschrittenen Schritt anzeigt. Wenn keine Zweier mehr in der Primfaktorzerlegung vorkommen, ist der obere Bereich dieser aufsteigenden Kette erreicht. Außerdem spielt die Anzahl der Dreien eine gegensätzliche Rolle: Sie zeigt an, wie viele Stufen bereits „aufgestiegen“ wurden. Durch das gezielte Austauschen von Zweien gegen Dreien und umgekehrt lässt sich die Struktur der Collatz-Kette quasi als Spiel mit Primfaktoren verstehen. Diese Sichtweise entwirrt die Verbindungen zwischen aufeinanderfolgenden Zahlen der Collatz-Folge und zeigt, wie bestimmte Zahlen miteinander verknüpft sind.
Ein weiteres überraschendes Ergebnis dieser Analyse ist, dass die Primfaktorzerlegung von c+1 nicht nur den Aufstieg innerhalb der Folge kontrolliert, sondern auch Hinweise auf den Weg rückwärts gibt. Das klassische Collatz-Verfahren ist zumeist vorwärtsgerichtet; das bedeutet, man kann nur schwer bestimmen, von welcher Zahl eine gegebene Zahl „kam“. Die Untersuchung der Primfaktoren erlaubt es jedoch, diesen Weg umzukehren und mögliche Vorgänger zu identifizieren, indem man Dreier wieder in Zweier umwandelt und daraus die Ausgangswerte ableitet. Betrachtet man große Zahlen und ihre Collatz-Sequenzen, wird das Zusammenspiel von Primfaktoren besonders deutlich. Viele Zahlenketten lassen sich in Abschnitte mit konstanten Grundstrukturen zerlegen, deren Unterschiede im Wesentlichen in der Zahl der Zweier und Dreier im Kontrollwert bestehen.
Dabei ergibt sich die Gesamtlänge eines aufsteigenden Abschnitts aus der Summe dieser beiden Faktoren. Eine interesssante Eigenschaft ist, dass die Primfaktorzerlegungen benachbarter Zahlen in der Folge oft sehr unterschiedlich sind. Dies erklärt, warum der Übergang von einer Zahl zur nächsten in der klassischen Darstellung der Collatz-Sequenz unregelmäßig wirkt. Die Faktoren der Kontrollwerte passen sich nämlich auf eine Weise an, die nicht einfach vorausgesagt werden kann, wodurch sich die Komplexität der Vermutung erklärt. Diese Erkenntnisse eröffnen neue Wege, um die Collatz-Vermutung zu verstehen.
Durch das Fokussieren auf Primfaktorzerlegungen wird die Folge in dynamische Ketten von Zahlen verwandelt, deren Verlauf von der Verteilung der Faktoren 2 und 3 bestimmt wird. Die Untersuchung der Muster und Übergänge dieser Faktoren könnte dazu beitragen, die Grenzen der Vermutung immer weiter einzugrenzen oder möglicherweise sogar einen Beweis zu liefern. Im weiteren Sinne spiegelt die Analyse der Collatz-Folge mittels Primfaktorzerlegungen eine grundlegende Eigenschaft vieler dynamischer Systeme wider: Hinter komplexen und chaotisch erscheinenden Prozessen können sich einfache Strukturen und Regeln verbergen. Die Betrachtung der Primfaktoren liefert ein Werkzeug, diese Strukturen zu entwirren und das Verhalten der Zahlenmengen systematisch zu erfassen. Zusammenfassend kann gesagt werden, dass die Primfaktorzerlegung von Zahlen in der Collatz-Sequenz nicht nur ein theoretisches Hilfsmittel ist, sondern ein zentrales Element, um die Vermutung besser zu verstehen.
Die Verknüpfung von Faktoren 2 und 3 steuert den Ablauf der Folge und zeigt Wege, wie man die scheinbare Unberechenbarkeit in berechenbare Muster überführen kann. Sollte sich diese Herangehensweise weiter bewähren, könnten mathematische Beweise, die auf der Primfaktorstruktur der Zahlen basieren, die Lösung für eines der großen offenen Probleme der Zahlentheorie bringen. Bis dahin schafft die Untersuchung der Primfaktorzerlegung nicht nur ein elegantes Interpretationsmodell, sondern bereichert auch das Verständnis für das faszinierende Verhalten der Collatz-Folge.