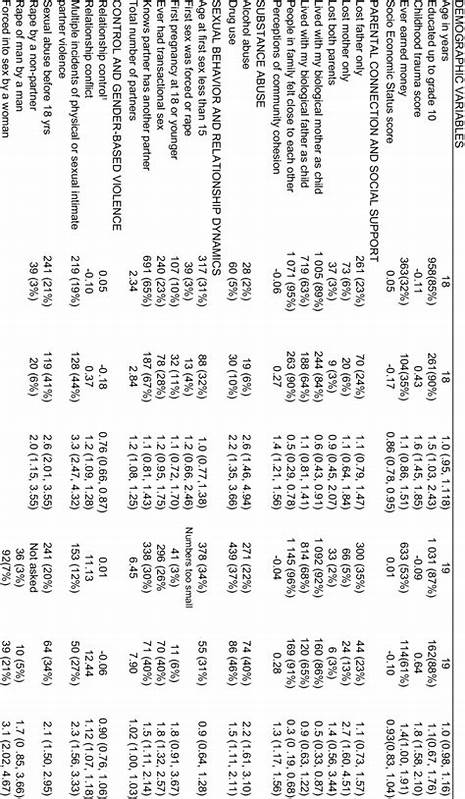
Die ganzzahlige lineare Programmierung (Integer Linear Programming, ILP) hat sich in den letzten fünfzig Jahren von einer eher theoretischen Disziplin zu einem zentralen Werkzeug in der Betriebsforschung und Entscheidungsfindung entwickelt. Die rasante Entwicklung von algorithmischen Verfahren und Rechenressourcen hat dazu geführt, dass Probleme, die vor Jahrzehnten noch unlösbar schienen, heute effizient und zuverlässig bearbeitet werden können. Dabei spielen moderne Mixed-Integer Linear Programming (MILP) Solver eine entscheidende Rolle, die in der Lage sind, selbst große und komplexe Probleme innerhalb von Sekunden optimal zu lösen. MILP vereint die Vorteile linearer Optimierung mit den Möglichkeiten, Variablen auf ganzzahlige Werte zu beschränken. Diese Eigenschaft ist für viele praktische Anwendungen unerlässlich, bei denen diskrete Entscheidungen getroffen werden müssen, wie zum Beispiel bei Ressourcenzuweisungen, Produktionsplanungen oder Logistiknetzwerken.
Die zunehmende Leistungsfähigkeit der MILP Solver hat die Tür zu neuen Anwendungsfeldern geöffnet, von der Transportoptimierung über Supply Chain Management bis hin zu Finanz- und Telekommunikationssystemen. Ein Schlüsselelement der Fortschritte im Bereich der ganzzahligen linearen Programmierung ist die Weiterentwicklung der sogenannten Branch-and-Cut-Verfahren. Diese kombinieren die klassische Branch-and-Bound-Methode mit sogenannten Schnitten (Cuts), die die Lösungsmenge einschränken und somit den Suchraum effizient reduzieren. Die letzten Jahrzehnte brachten zahlreiche Innovationen in der Art und Weise, wie Schnitte generiert und angewendet werden, was eine erhebliche Leistungssteigerung bei der Lösung großer MILP-Probleme ermöglicht hat. Parallel dazu haben sich Dantzig-Wolfe- und Benders-Zerlegungen als kraftvolle Werkzeuge etabliert, um große und komplexe Probleme durch Zerlegung in kleinere, besser handhabbare Teilprobleme zu lösen.
Diese Methoden nutzen die Struktur der zu optimierenden Modelle aus und ermöglichen damit, Probleme zu bearbeiten, die mit klassischen Ansätzen kaum bewältigbar wären. Neuere Forschungsansätze konzentrieren sich darauf, diese Zerlegungsverfahren noch effizienter zu gestalten und mit modernen Branch-and-Cut-Algorithmen zu kombinieren. Ein weiterer bedeutender Fortschritt besteht in der Integration von heuristischen Verfahren mit exakten Algorithmen. Während exakte Methoden globale Optimalität garantieren, können heuristische Ansätze in kürzerer Zeit gute Lösungen liefern. Die Kombination dieser beiden Welten in hybriden Algorithmen trägt dazu bei, die Gesamtlaufzeit zu reduzieren und die Lösungsqualität zu verbessern.
Machine Learning und künstliche Intelligenz werden zunehmend genutzt, um Entscheidungen innerhalb der Algorithmen zu optimieren, etwa bei der Wahl von Schnitten oder Variablen zum Branching. Moderne Softwarepakete für MILP profitieren zudem von erheblicher Hardwareentwicklung. Die Nutzung paralleler Rechenarchitekturen und Cloud-Computing ermöglicht es, rechenintensive Optimierungsaufgaben an externe Server auszulagern und so die Berechnungszeiten drastisch zu verringern. Veränderungen in der Softwarearchitektur sorgen dafür, dass heutige MILP-Solver auf verschiedenen Plattformen skalierbar und anpassbar sind, was zu einer breiteren Verfügbarkeit und Anwendung beiträgt. Die praktischen Anwendungen der ganzzahligen linearen Programmierung haben in den letzten Jahren einen enormen Zuwachs erfahren.
In der Transport- und Logistikbranche unterstützen ILP-Modelle die Routenplanung, Ladungsoptimierung und das Flottenmanagement. Im Supply Chain Management ermöglicht MILP eine präzise Planung von Lagerbeständen, Produktionskapazitäten und Lieferterminen. Darüber hinaus finden sich Anwendungen in der Finanzbranche für Portfoliooptimierung und Risikomanagement, in Produktionsumgebungen zur effizienten Nutzung von Ressourcen sowie in Telekommunikationsnetzen für Bandbreitenzuweisung und Netzwerkdesign. Die Zukunft der ganzzahligen linearen Programmierung verspricht weitere spannende Entwicklungen. Die kontinuierliche Verbesserung von Algorithmen, die Integration von Data-Science-Technologien und neue Modellierungstechniken werden es ermöglichen, noch komplexere und realitätsnähere Problemstellungen zu bewältigen.
Gleichzeitig stellen die steigende Komplexität von Anwendungsfällen und die wachsende Datenmenge Herausforderungen dar, denen die Forschung durch innovative Ansätze begegnet. Insgesamt zeigt die Entwicklung der letzten fünfzig Jahre, dass ganzzahlige lineare Programmierung ein dynamisches und sich ständig weiterentwickelndes Feld ist, das entscheidende Beiträge zur Lösung praktischer Optimierungsprobleme leistet. Die effektive Kombination von theoretischem Fortschritt, technologischem Fortschritt und realer Anwendung macht MILP auch heute zu einem der wichtigsten Werkzeuge moderner Entscheidungsunterstützungssysteme.