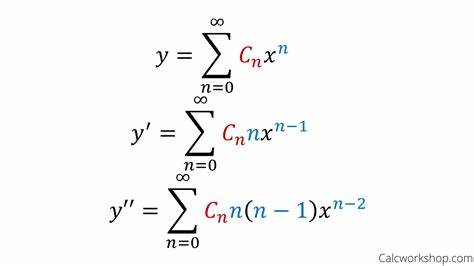Die Mathematik hat seit jeher versucht, Lösungen für Polynomgleichungen zu finden – vom quadratischen Binom bis hin zu komplexen höheren Graden. Besonders faszinierend ist dabei die Verbindung zwischen Algebra und Kombinatorik, die eine völlig neue Sichtweise eröffnet: die Verwendung der Hyper-Catalan-Reihe zur Lösung allgemeiner Polynomgleichungen. Dabei spielt ein herausragendes algebraisch-kombinatorisches Objekt, genannt die Geode, eine zentrale Rolle, das tiefere Einblicke in die Natur dieser Zahlenfamilie ermöglicht. Diese innovative Methodik hebt sich deutlich von klassischen Lösungsansätzen wie der Radikalmethode ab und macht dort weiter, wo die traditionelle Algebra gemäß den Erkenntnissen von Galois endet. Ursprünge und Geschichte der Hyper-Catalan-Zahlen Die traditionellen Catalan-Zahlen sind seit dem 18.
Jahrhundert bekannt und zählen verschiedene kombinatorische Strukturen, insbesondere die Anzahl der möglichen Triangulierungen eines Polygons. Ihre Anwendung in der Lösung der quadratischen Gleichung ist ebenso elegant wie lehrreich. So ist es beispielsweise bekannt, dass die Generating-Funktion der Catalan-Zahlen eine Lösung einer quadratischen Gleichung darstellt. Doch diese Zahlen bilden nur den Anfang einer weitaus größeren Struktur. Die Hyper-Catalan-Zahlen erweitern dieses Konzept, indem sie nicht nur Triangulierungen sondern auch Zerlegungen eines Polygons in verschiedenartige Teilpolygone – darunter Quadrilaterale, Pentagone und so weiter – zählen.
Bereits im 19. und frühen 20. Jahrhundert wurden von Mathematikern wie Erdélyi und Etherington bis hin zu Kreweras und Tutte bedeutende Fortschritte in der Erforschung dieser Zahlen gemacht. Allerdings blieben viele ihrer faszinierenden Eigenschaften bislang weitgehend unerforscht oder wurden nicht mit der Lösung allgemeiner Polynomgleichungen in Verbindung gebracht. Die Kombinatorische Geometrie des Polygonzerlegens Die Grundlage für die Hyper-Catalan-Zahlen bildet die Betrachtung sogenannter Subdigone: konvexe, dachförmig orientierte Polygone, die durch nicht-kreuzende Diagonalen in kleinere Polygonflächen unterschiedlicher Art zerlegt sind.
Jeder solcher Subdigon-Typ lässt sich durch einen unendlichen Vektor beschreiben, dessen Einträge die Anzahl der enthaltenen Dreiecke, Vierecke, Fünfecke usw. angeben. Durch die Anwendung eines algebraischen Operators, der als Panelling-Operator bezeichnet wird, können diese kleineren Teilpolygone auf vielfältige Weise miteinander kombiniert werden, um größere Subdigone zu formen. Die zugehörige algebraische Struktur lässt sich in einen Formalismus übertragen, der die Bildung von Potenzreihen über einer Vielzahl von Variablen ermöglicht. Diese Mächtigkeit erlaubt es, eine sogenannte Subdigon-Polyserie zu definieren, die als Generating-Funktion der Hyper-Catalan-Zahlen fungiert.
Diese Polyserie löst formal eine unendliche polynomiale Gleichung, deren Variablen mit den unterschiedlichen Polygonarten bzw. Panellings korrespondieren. Die Hyper-Catalan-Serie als Lösung von Polynomgleichungen Der wesentliche Durchbruch liegt darin, dass sich allgemeine univariate Polynomgleichungen mit Hilfe dieser Hyper-Catalan-Serie formal lösen lassen. Während klassische Methoden nach Radikalen suchen, die gemäß dem Satz von Abel-Ruffini für Polynome höheren Grades ab dem fünften Grad im Allgemeinen nicht existieren, setzt die Hyper-Catalan-Methode auf unendliche Potenzreihenlösungen, die formal jede Polynomgleichung repräsentieren. Die Gleichung hat dabei stets die Struktur 0 = 1 - α + t₂α² + t₃α³ + t₄α⁴ + .
.. wobei die tₖ Variablen symbolisch für die Gewichtung der jeweiligen Polygonflächenarten stehen. Die Lösung α ergibt sich dann als formale Potenzreihe mit den Hyper-Catalan-Zahlen als Koeffizienten, die aus der Anzahl entsprechender Polygonzerlegungen hervorgehen. Diese Darstellung ist weit mehr als eine bloße theoretische Kuriosität.
Sie erlaubt nämlich eine explizite, geschlossene Form der Koeffizienten, die sich in geschickter Weise kombinatorisch interpretieren lassen. Daraus folgt unmittelbar ein universelles Lösungsschema für Polynomgleichungen beliebigen Grades, das bisherige klassische Beschränkungen überwindet. Kombinatorische Formeln und der Einfluss der Euler’schen Polyederformel Die Hyper-Catalan-Zahlen besitzen eine bemerkenswerte geschlossene Formel, die eng mit der Euler’schen Polyederformel zusammenhängt, welche eine fundamentale Beziehung zwischen der Anzahl von Ecken, Kanten und Flächen eines Polygons oder Polyeders beschreibt. Genauer lässt sich jeder Hyper-Catalan-Koeffizient durch Fakultätsquotienten ausdrücken, die die Vertex-Edge-Face-Struktur der passenden Subdigone kodieren. Diese Verbindung ist keineswegs zufällig, sondern zeigt, wie tief die Topologie und Kombinatorik eines Polygons mit den algebraischen Lösungen zusammenhängen.
Durch geeignete Variablenersetzungen lässt sich die allgemeine Polynomgleichung in eine Version überführen, die formal genau von dieser Hyper-Catalan-Reihe gelöst wird. Die Geode: Ein Mysterium in der Algebra der Hyper-Catalan-Zahlen Die Untersuchung der Hyper-Catalan-Polyserie nach weiteren inneren Strukturen führt zur Entdeckung eines neuen algebraisch-kombinatorischen Arrays, das als Geode bezeichnet wird und die Hyper-Catalan-Zahlen fundamentaler kodiert. Die Geode taucht auf, wenn man die Serie nach der Anzahl der Flächen schichtet – also die Hyper-Catalan-Serie „nach Ebenen“ zerlegt. Dabei zeigt sich eine erstaunliche Faktorisierung, die nahelegt, dass die Geode selbst ein eigenständiges mathematisches Objekt mit tieferem Bedeutungsgehalt ist. Ihre Einträge scheinen mit speziellen geordneten unvollständigen Bäumen verbunden zu sein und weisen unregelmäßige, teils enorm große Primfaktoren auf, was auf eine sehr komplexe innere Struktur hinweist.
Mathematische Vermutungen und offene Fragen zu Geode und Hyper-Catalan Während klare Formeln für die Hyper-Catalan-Zahlen existieren, ist die genaue Bestimmung der Geode-Zaheln nach wie vor Gegenstand aktueller Forschung und Konjekturen. Ein Teil der mathematischen Gemeinschaft vermutet, dass die Geode als kodierende Struktur für gewisse Klassen von Bäumen oder Polygonzerlegungen dienen könnte, möglicherweise eng verknüpft mit nichtkreuzenden Partitionen und anderem combinatorischen Geflecht. Ebenso interessant ist die Frage, wie diese reiche Kombinatorik mit der klassischen Galois-Theorie harmoniert, die ja die Grenzen algebraischer Lösbarkeit mit Radikalen charakterisiert. Die Hyper-Catalan-Reihenlösung eröffnet hier eine ganz andere Perspektive: Nicht die endlich-radikale Lösbarkeit, sondern die unendliche Potenzreihen-Darstellung der Lösungen rückt in den Mittelpunkt. Praktische Anwendung und numerische Approximation Trotz der abstrakten Natur bietet das Konzept auch praxisorientierte Vorteile.
So lässt sich etwa die Hyper-Catalan-Reihe verwenden, um numerische Approximationen von Polynomwurzeln systematisch zu erzeugen. Dabei kann man mit nur wenigen Gliedern der Reihe eine erste Näherung erhalten, die durch wiederholtes „Bootstrapping“ – also das Einsetzen verbesserter Ergebnisse in den Ausgangsausdruck – schnell zu hoher Genauigkeit konvergiert. Ein Beispiel ist die Berechnung der Wurzeln kubischer Gleichungen nach Wallis, bei der selbst eine begrenzte Anzahl an Koeffizienten der Hyper-Catalan-Reihe zu numerisch präzisen Lösungen führt. Damit stellt die Methode eine interessante Alternative zu klassischen numerischen Verfahren wie dem Newton-Raphson-Verfahren dar. Weiterhin ermöglicht die Verbindung zu Lagrange’scher Inversionstechnik eine elegante theoretische Begründung der Formalreihen und deren Koeffizienten, die auf ältere mathematische Methoden zurückgreift und diese gleichzeitig weit übertrifft.
Zukunftsperspektiven und Bedeutung für die Mathematik Die Erforschung der Hyper-Catalan-Reihen und der Geode bietet einen verheißungsvollen Pfad für die Weiterentwicklung der Algebra, Kombinatorik und numerischen Mathematik. Sie stellen eine Brücke dar zwischen rein algebraischen Fragen, geometrisch-kombinatorischen Strukturen und praktischen Rechenmethoden. Darüber hinaus regt diese Arbeit dazu an, das Umfeld der katalanischen Zahlreihen in der Online-Enzyklopädie der Integer-Sequenzen (OEIS) systematisch um Hyper-Catalan-bezogene Folgen zu erweitern. Dies könnte die Entdeckung neuer Zusammenhänge fördern und eine tiefere Einsicht in die vielfältigen Erscheinungsformen dieser Zahlen und ihrer Objekte bieten. Abschließend lässt sich festhalten, dass die Hyper-Catalan-Reihentechnik nicht nur als universelles Werkzeug zur Lösung von Polynomgleichungen dient, sondern auch als Keim für neue Theorien in der Kombinatorik und Algebra.
Sie trägt zum Umdenken hinsichtlich der Lösbarkeit von Gleichungen bei und fordert traditionelle Paradigmen heraus, indem sie formal unendliche Reihenlösungen statt endliche Radikale in den Vordergrund rückt. Die Adaption und Vertiefung dieser Methoden in Lehre, Forschung und angewandte Mathematik wird mit großer Wahrscheinlichkeit eine Vielzahl an neuen Erkenntnissen hervorbringen und die vernetzte Sicht auf algebraische, kombinatorische und analytische Strukturen weiter festigen.