In der Welt der Computerspiele spielt Geschwindigkeit eine entscheidende Rolle. Besonders in der 3D-Grafik, wo Rechenoperationen millionenfach pro Sekunde durchgeführt werden müssen, sind effiziente Algorithmen unverzichtbar. Eines der bemerkenswertesten Beispiele für solche Optimierungen findet sich im Kultspiel Quake aus den 90er Jahren. Quake verwendete eine verblüffend schnelle Methode zur Berechnung der inversen Quadratwurzel, die direkt die Leistung der Grafik-Engine verbesserte. Doch was steckt hinter diesem scheinbar magischen Algorithmus, wie funktioniert er und warum ist er so schnell? Tauchen wir tiefer in die Mathematik und Computertechnik hinter Quakes Fast Inverse Square Root ein.
Warum ist die inverse Quadratwurzel in Spielen wichtig? Viele 3D-Programme müssen Vektoren normalisieren – das heißt, deren Länge auf 1 setzen, um Richtungen zu definieren, ohne die Skalierung zu verändern. Die Länge eines Vektors wird mit Hilfe des Satzes von Pythagoras berechnet und beinhaltet eine Quadratwurzel. Für eine Normalisierung wird nicht die Länge selbst, sondern die inverse Länge benötigt, die man erhält, wenn man durch die Quadratwurzel dividiert. Da diese Operation tausendfach pro Frame und Frame pro Sekunde ausgeführt wird, summiert sich jedes kleine Zeitersparnis enorm. Normale Berechnungen der Quadratwurzel sind auf heutigen Prozessoren immer noch relativ teuer und können durch Multiplikationen und Bitmanipulationen manchmal deutlich beschleunigt werden.
Die Fast Inverse Square Root Funktion von Quake erlangte Ruhm durch ihre Kombination aus mathematischem Know-how und technischen Tricks. Der Kern dieser Methode basiert auf einer cleveren Schätzung in Kombination mit einer Iteration des Newton-Raphson-Verfahrens, einem universellen numerischen Verfahren zur schnellen Annäherung an Nullstellen von Funktionen. Im Falle der inversen Quadratwurzel führt ein sorgfältig gewählter Startwert zu einer extrem schnellen Konvergenz auf den exakten Wert. Die Implementierung der Funktion wirkt auf den ersten Blick fast wie Zauberei: Eine Fließkommazahl wird als ganze 32-Bit-Zahl interpretiert, Bitverschiebungen werden benutzt, um exponentielle Operationen zu ersetzen, und eine sogenannte magische Konstante korrigiert das Ergebnis. Dieses Vorgehen basiert auf der Tatsache, dass Fließkommazahlen intern in einem speziellen Format abgespeichert werden, das Mantisse und Exponent getrennt hält.
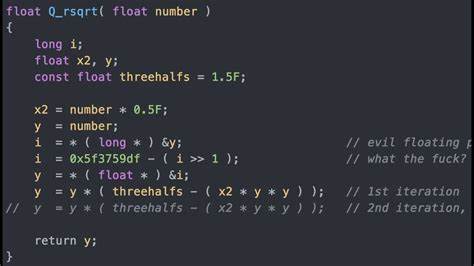
Anstatt teure Rechenoperationen auf reales Gleitkomma durchzuführen, werden Interimsschritte als Ganzzahlen behandelt, was große Geschwindigkeitsvorteile bringt. Im Quellcode sieht die Funktion folgendermaßen aus: Zunächst wird die halbe Eingabe berechnet und die Fließkommdaten werden als Integerbits interpretiert. Dann wird der Integerwert mit der magischen Zahl 0x5f3759df manipuliert, die sozusagen den exponentiellen Mittelwert für die Inverse festlegt. Der Vorgang der Bitverschiebung halbiert quasi den Exponenten – da der Exponent in Gleitkommazahlen in binären Schritten gespeichert ist, entspricht ein Rechts-Shift etwa einer Division durch zwei. Durch die Subtraktion von der magischen Zahl wird diese geteilte, aber noch unverzerrte Form in eine Vernünftige Nährung verwandelt.
Anschließend wird der Integerwert wieder zurück in eine Fließkommazahl umgewandelt und eine Iteration einer verbesserten Näherung mittels Newtons Methode durchgeführt. Newton-Raphson ist ein Verfahren, welches aus einer ersten Schätzung Schritt für Schritt eine bessere Schätzung für eine Funktion liefert. Im Fall der inversen Quadratwurzel wird eine Funktion definiert, deren Nullstelle genau dem berechneten Wert entspricht. Dabei nutzt die Methode die Ableitung der Funktion, um zu ermitteln, in welche Richtung sich die Schätzung hinbewegen muss. Die Formel, die gestartet wird, lautet x = x * (1.
5f - (xhalf * x * x)), wobei x die vorläufige Schätzung ist und xhalf die halbe ursprüngliche Zahl. Diese eine Iteration genügt, da der Startwert bereits sehr nahe am exakten Wert liegt und weitere Iterationen nur minimalen Gewinn für erheblichen Rechenaufwand bringen würden. Das Herzstück der Geschwindigkeit liegt also im Startwert, der aus der Bitinterpretation der Gleitkommazahl abgeleitet wird und der magischen Zahl. Diese magische Zahl ist das Ergebnis umfangreicher Versuche und Optimierungen, um den Fehler im Startwert zu minimieren. Durch sie wird nicht nur der exponentielle Teil angepasst, sondern auch Fehler ausgeglichen, die durch binäre Rundungen und Ungenauigkeiten in der Darstellung entstehen.
Tatsächlich existieren Varianten der magischen Zahl, die für unterschiedliche Präzisionsanforderungen entwickelt wurden, doch die Version aus Quake ist bis heute die berühmteste. Das Verfahren ist nicht nur ein cleverer Hack, sondern demonstriert einen wichtigen Aspekt moderner Programmierung: die Nutzung von tiefem technischen Verständnis gepaart mit mathematischen Methoden, um die bestmögliche Performance zu erzielen. Es zeigt auch, wie systemnahe Programmierung Vorteile bringt, die auf höheren Abstraktionsebenen kaum möglich sind. Ein weiteres interessantes Detail ist die Tatsache, dass die Implementierung vollkommen ohne teure Divisionen oder Wurzeln auskommt. Stattdessen wird mit einfachen Operationen wie Bitverschiebungen, Subtraktionen und Multiplikationen gearbeitet.
In Zeiten, in denen Prozessoren deutlich langsamer waren als heute, waren solche Optimierungen essenziell. Auch heute können solche Tricks in zeitkritischen Anwendungen wie Spielen, Simulationen oder wissenschaftlichen Programmen von großem Vorteil sein. Natürlich ist die Methode nicht fehlerfrei und liefert nur eine Approximation. Doch für die meisten Anwendungen, bei denen die inverse Quadratwurzel verwendet wird, ist eine höhere Genauigkeit als sie durch die Kombination von magischem Startwert und einer Newton-Iteration erreicht wird, nicht nötig. Dies gilt besonders in Spielen, wo kleine Ungenauigkeiten visuell kaum auffallen, während Performance sehr wohl spürbar verbessert wird.
Die Popularität dieser Methode hat im Internet zu zahlreichen Diskussionen und Analysen geführt. Viele Entwickler haben die Umsetzung studiert, variiert und sogar verbessert. Es zeigt, wie ein einzelner Algorithmus weit über sein ursprüngliches Einsatzgebiet hinaus Inspiration liefern kann. Die Fast Inverse Square Root ist mittlerweile fast eine Legende und ein Paradebeispiel für clevere Algorithmen in der Computergrafik und Programmierung. Abschließend lässt sich sagen, dass die schnelle inverse Quadratwurzel von Quake ein Meilenstein im Bereich der effizienten Algorithmen ist.
Durch geschicktes Nutzen der internen Struktur von Gleitkommazahlen und Anwendung einer einzigen Newtonschen Optimierung wird eine schnelle und ausreichend genaue Schätzung ermöglicht. Dieses Verfahren veranschaulicht eindrucksvoll, wie tiefgründige Mathematik und systemnahe Programmierung zusammenkommen können, um praktische Probleme zu lösen. Wer sich mit der Optimierung von Algorithmen beschäftigt, sollte dieses Beispiel unbedingt kennen – es zeigt, dass manchmal die besten Lösungen jene sind, die mit Mut zu ungewöhnlichen Wegen und Verständnis der zugrundeliegenden Mechanismen entstehen.