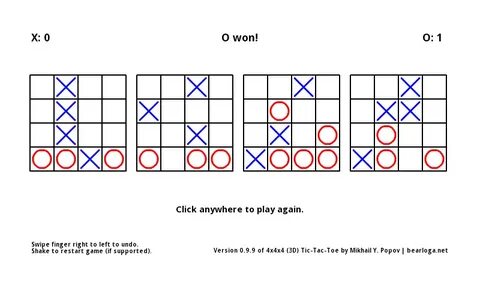
Tic-Tac-Toe ist eines der bekanntesten und am meisten gespielten Strategiespiele weltweit. Während die klassische Variante auf einem 3x3 Raster stattfindet und für erfahrene Spieler meist in einem Unentschieden endet, erweitert die dreidimensionale Version auf einem 4x4x4 Spielfeld die Komplexität enorm. Dieses Spiel wird auf einem Würfel aus 64 Zellen gespielt, bei dem der Versuch besteht, vier eigene Symbole in eine gerade Linie zu bringen. Diese Linie kann horizontal, vertikal, diagonal oder sogar entlang der Raumdiagonalen verlaufen, was die taktischen Möglichkeiten vielfältig und ausgesprochen spannend macht. Die größte Herausforderung besteht darin, eine Strategie zu entwickeln, mit der der erste Spieler stets gewinnen kann, unabhängig von den Zügen des Gegners.
Im Gegensatz zum klassischen 3x3 Tic-Tac-Toe, das bei perfektem Spiel beider Seiten immer unentschieden ausgeht, stellt 4x4x4 Tic-Tac-Toe eine andere Herausforderung dar. Es ist mathematisch bewiesen, dass der zweite Spieler, häufig mit dem Symbol „O“ versehen, niemals gewinnen kann, wenn der erste Spieler, symbolisiert durch „X“, optimal spielt. Allerdings sagt die sogenannte Strategie-Diebstahl-Argumentation aus der Spieltheorie nur aus, dass „O“ nicht gewinnen kann. Ob das Spiel zwangsläufig mit dem Sieg für „X“ endet oder in einem Unentschieden aufgeht, bleibt dabei zunächst unklar – ein Punkt, den die Forschung lange beschäftigte. Erst in den späten 1970er Jahren gelang Oren Patashnik der Durchbruch.
Mit Computern als Werkzeug erarbeitete er eine komplette Strategie für den ersten Spieler, die „X“ zum sicheren Sieg führt. Dieser bahnbrechende Beweis wurde in einer Veröffentlichung mit dem Titel „Qubic: 4x4x4 Tic-Tac-Toe“ zusammengefasst. Doch nicht nur die Theorie, sondern auch die praktisch nachvollziehbaren Züge dieser Strategie wurden dokumentiert und als Textdatei veröffentlicht, die eine umfassende Schritt-für-Schritt-Anleitung für „X“ darstellt. Das Wesen einer solchen Strategie liegt darin, für jede mögliche Spielsituation die optimale Antwort zu kennen. Dies geschieht durch eine sogenannte Positionsdatei oder Strategie-Dictionary, in der jeder denkbare Zustand des Spiels einem besten Zug zugeordnet wird.
In der Praxis ist es allerdings kaum möglich, jede Position einzeln zu speichern. Die Anzahl der möglichen Spielverläufe ist schier gigantisch. Um dies handhabbar zu machen, greifen Entwickler auf symmetrische Abbildungen, Drehungen und Spiegelungen des Spielfelds zurück. Dadurch können gleichartige Situationen zusammengefasst und die Datenmenge erheblich reduziert werden. Eine besonders clevere Methode zur Komprimierung ist die Nutzung von Muster-Markierungen.
Zum Beispiel werden die Positionen, in denen der zweite Spieler (O) seinen Zug machen könnte, mit einem gemeinsamen Symbol „O“ zusammengefasst. Dadurch lassen sich mehrere ähnliche Spielsituationen in einem Eintrag darstellen. Die Strategie für den ersten Spieler kann somit sehr knapp und effizient dargestellt werden, was eine Übersichtlichkeit schafft und den Computer dazu befähigt, schnell die optimale Antwort zu geben. Patashniks ursprüngliches Programm erreichte eine Kompaktheit von lediglich 2929 Zeilen, was bereits für damalige Computertechnik revolutionär war. Später gelang es mithilfe von erweiterten Kompressionstechniken und besserem Nutzen symmetrischer Situationen, diese Zahl auf unter 1000 Zeilen zu reduzieren.
Dieser Fortschritt zeigt eindrucksvoll, wie Mathematik und Informatik Hand in Hand gehen, um komplexe Spiele handhabbar zu machen. Die praktische Umsetzung eines so detaillierten Dictionaries ermöglicht die Erstellung eines für den Menschen kaum zu besiegenden Computergegners. Ein Algorithmus liest die aktuelle Spielsituation, erkennt über Transformationen die passende Eintragung im Wörterbuch und schlägt den optimalen Zug vor. Ist die Position nicht im Wörterbuch enthalten, werden logische Schlussfolgerungen herangezogen, um sicherzustellen, dass keine Fehler gemacht werden. Dabei muss das Programm mit sogenannten „erzwungenen Zügen“ oder „gezwungenen Folgen“ umgehen können, bei denen ein Spieler gezwungen ist, einen bestimmten Zug zur Blockade eines drohenden Gewinns zu machen.
Die Herausforderung für Entwickler liegt darin, das Wörterbuch maximal kompakt zu speichern, gleichzeitig aber alle relevanten Spielpositionen abzudecken. Werden Lücken gelassen, könnten dem Programm Fehler unterlaufen, die von einem erfahrenen Spieler ausgenutzt werden könnten. Ein weiteres Ziel besteht darin, nicht nur den ersten Spieler X optimal zu machen, sondern auch Strategien zu entwickeln, die optimale Antworten auf unterschiedliche Züge des Gegners bieten. Neben dem Einsatz in Computerspielen bietet die Erforschung von 4x4x4 Tic-Tac-Toe auch tiefe Einblicke in die Spieltheorie, Algorithmik und mathematische Beweisverfahren. Das Projekt exemplifiziert, wie Computersimulationen und formale Methoden eingesetzt werden können, um komplexe Probleme zu analysieren und zu lösen.
Dies ist insbesondere bei Spielen mit hoher Komplexität, wie etwa Schach oder Go, von Bedeutung. Die weiterführende Idee, die Kompression und Vereinfachung der Dictionaries noch weiter voranzutreiben, stellt eine anhaltende Herausforderung an Informatiker und Mathematiker dar. Einige der offenen Fragen beschäftigen sich mit der optimalen Algorithmik für die Komprimierung solcher Datensätze und der Frage, ob deren Bearbeitung in der Praxis überhaupt effizient möglich ist, ohne wichtige Informationen zu verlieren. Gewisse Ansätze deuten darauf hin, dass eine vollständige Kompression möglicherweise NP-schwer ist, was bedeutet, dass es keine effiziente Lösung gibt, die das optimale Ergebnis garantiert. Die Erforschung von 4x4x4 Tic-Tac-Toe und seiner Gewinnstrategien ist auch ein ideales Betätigungsfeld für Programmierwettbewerbe und algorithmische Herausforderungen wie zum Beispiel die Advent of Code Challenge.
Die Umsetzung verschiedener Aufgaben, wie das Komprimieren einer Strategiesammlung, das Prüfen der Vollständigkeit eines Wörterbuchs oder das Erstellen einer „unbesiegbaren“ KI, erfordern sowohl fachliches Wissen als auch kreatives Problemlösungsverhalten. Auf GitHub und ähnlichen Plattformen sind zudem verschiedene Tools und Programme zugänglich, die diese Materie aufgreifen und als Ausgangspunkt für eigene Experimente dienen können. Dabei sind viele Werkzeuge noch in einem frühen Entwicklungsstadium und laden zu weiteren Verbesserungen und Erweiterungen ein. Die Verbindung zwischen solchen mathematisch anspruchsvollen Problemen und der Unterhaltung durch Spiele zeigt eindrucksvoll, wie vielseitig der Bereich der Informatik sein kann. Während das Gewinnen bei 4x4x4 Tic-Tac-Toe vielleicht auf den ersten Blick wie ein simples Ziel erscheint, erfordert es doch tiefes Verständnis, präzise Analyse und innovative Programmierung.
Das Spiel projiziert damit eine spannende Brücke zwischen der spielerischen Welt des Freizeitabenteuers und der analytischen Tiefe der wissenschaftlichen Forschung. Die Erkenntnisse, die durch die Untersuchung solch eines Spiels gewonnen werden, haben Potenzial weit darüber hinaus, etwa bei der Optimierung von Suchalgorithmen, Mustererkennung oder künstlicher Intelligenz. Zusammengefasst kann gesagt werden, dass 4x4x4 Tic-Tac-Toe weit mehr als nur ein Spiel ist. Es ist ein faszinierendes Forschungsgebiet, eine Herausforderung für Programmierer und ein wunderbares Beispiel für die Kombination von theoretischer Mathematik mit praktischer Informatik. Die Möglichkeit, durch ein „Orakel“, nämlich das ausgefeilte Strategie-Dictionary, einen bestimmten Sieg zu garantieren, ist ein Meilenstein in der Algorithmik und der spielerischen Mathematik.
Die weitere Erforschung und das Spiel mit solchen Strategien verspricht auch in Zukunft spannende Einblicke und unterhaltsame Herausforderungen für Spieleliebhaber wie Forscher. Ob als Inspiration für komplexere Spiele, als Testfeld für KI oder einfach als faszinierendes Denkspiel – 4x4x4 Tic-Tac-Toe bleibt eine bemerkenswerte Perle in der Welt der Spieltheorie und Computermathematik.