Layer Normalization hat sich in den letzten Jahren als eine essentielle Technik zur Stabilisierung und Beschleunigung von tiefen neuronalen Netzwerken etabliert. Im Gegensatz zur Batch Normalization, die über eine Batch von Trainingsbeispielen normalisiert, erfolgt die Layer Normalization innerhalb einzelner Eingabeschichten und ist dadurch besonders für sequenzielle Daten und Anwendungen wie NLP oder RNN-basierte Modelle geeignet. Das Verständnis der Gradientenableitung im Backward Pass ist entscheidend, um Layer Normalization korrekt implementieren und optimieren zu können. In diesem umfangreichen Beitrag wird der gesamte Prozess der Gradientenbildung beim Backward Pass von Layer Normalization detailliert erläutert, angefangen bei einer Wiederholung des Forward Pass, bis hin zur komplexen Herleitung der partiellen Ableitungen mit dem Fokus auf eine klare mathematische und konzeptionelle Darstellung. Zu Beginn betrachten wir die Grundformel der Layer Normalization für einen einzelnen Eingabevektor x mit der Dimensionalität N.
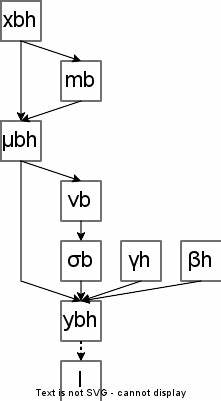
Die Normalisierung beruht auf der Berechnung des Mittelwerts μ und der Varianz σ² innerhalb dieses Vektors, gefolgt von einer Skalierung und Verschiebung mit trainierbaren Parametern γ und β. Die Formel für die Ausgabe y lautet: y = (x - μ) / √(σ² + ϵ) * γ + β. Hierbei sorgt der Zusatz ϵ für numerische Stabilität und verhindert Divisionen durch Null. Der Mittelwert μ wird als durchschnittlicher Wert aller Elemente xj berechnet, die Varianz σ² gibt die Streuung um den Mittelwert an und dient der Normierung, um die Verteilung der Aktivierungen zu standardisieren. Im Training ist der Backward Pass maßgeblich für die Anpassung der Modellparameter durch die Berechnung der Gradienten der Verlustfunktion bezüglich der Eingaben und Parameter.
Die Herausforderung bei Layer Normalization besteht darin, dass jedes Element xj nicht nur direkt die Ausgabe yj beeinflusst, sondern auch indirekt über die berechneten Mittelwerte und Varianzen alle anderen Ausgabekomponenten mitbestimmt. Deshalb müssen die Ableitungen mit Rücksicht auf diesen vernetzten Einfluss sorgfältig hergeleitet werden. Ein wichtiger Bestandteil der Backward-Pass-Berechnung betrifft die Gradienten bezüglich der Skalierungs- und Verschiebungsparameter γj und βj. Diese lassen sich relativ leicht bestimmen, da γ und β ausschließlich in der letzten Verarbeitungsstufe agieren. Die partiellen Derivate von y bezüglich γj und βj sind direkt an den normalisierten Eingang x^j gebunden.
Daraus folgt, dass die Gradienten dL/dγj und dL/dβj sich als Summen über das Produkt der Fehlergradienten dL/dyj mit den jeweiligen partiellen Ableitungen berechnen lassen. In der Praxis, bei Verwendung von Mini-Batches, werden die Gradienten über alle Batch-Elemente aufsummiert, da γ und β als Parameter der Schicht über die gesamte Batch geteilt werden. Die Ableitung dL/dx^j der Verlustfunktion bezüglich des normalisierten Eingangs ist ebenfalls recht unmittelbar: Sie wird als Produkt von dL/dyj und γj definiert, da γj die gewichtete Rolle im Transformationsschritt spielt. Die eigentliche Herausforderung liegt jedoch in der Berechnung von dL/dxj, also dem Gradienten bezüglich der ursprünglichen Eingangssignale xj. Aufgrund der Berechnung von μ und σ² über alle Elemente des Eingabevektors x, beeinflusst eine Veränderung von xj sämtliche Elemente der Normalisierung.
Durch Anwendung der Kettenregel und Berücksichtigung der gegenseitigen Abhängigkeiten entsteht eine komplexe Gleichung, welche die partiellen Ableitungen von μ und σ² nach xj benötigt. Der Ableitungsprozess verwendet das Produkt- und Summenregel-Prinzip und macht explizit die Ableitung der inversen Standardabweichung rstd = 1 / √(σ² + ϵ) nach den einzelnen xj sichtbar. Von zentraler Bedeutung ist die Erkenntnis, dass aufgrund der Definition von μ als Mittelwert und der Tatsache, dass die Summe der Abweichungen ∑(x_p - μ) null ist, einzelne Terme in den Ableitungen wegfallen, was die endgültige Herleitung vereinfacht. Die finale verdichtete Formel für den Gradienten dL/dxj zeigt, dass dieser als eine gewichtete Kombination von drei wesentlichen Komponenten verstanden werden kann: Der direkte Einfluss von dL/dx^j, die mittlere Wirkung aller dL/dx^k über die Batch-Dimension und die gewichtete Summe der Produkte aus den Gradienten dL/dx^k mit den normalisierten Eingaben x^k. Diese Kombination wird durch die inverse Standardabweichung rstd skaliert, was den reellen Einfluss der Varianz auf die Gradienten verdeutlicht.
Das Resultat erleichtert die effiziente Umsetzung des Backpropagation-Algorithmus für Layer Normalization erheblich, da es mögliche Redundanzen vermeidet und klar definiert, wie lokale und globale Einflüsse im Eingaberaum zu berücksichtigen sind. Die Bedeutung dieser Herleitung liegt nicht nur in der theoretischen Eleganz, sondern auch in praktischen Implikationen für Trainingseffizienz und Modellstabilität. Insbesondere bei tiefen und komplexen Architekturen, wie Transformern oder rekurrenten neuronalen Netzen, spielt die genaue Berechnung der Gradienten eine enorme Rolle für den Lernerfolg und die Vermeidung von Explodieren oder Verschwinden der Gradienten. Durch die Anwendung der ausführlich hergeleiteten Formeln können Entwickler und Forscher Layer Normalization implementieren, die nicht nur robuste Vorwärtsberechnungen liefert, sondern auch genaue und stabile Gradienten für den Rückwärtsschritt. Dies fördert eine bessere Konvergenzgeschwindigkeit und höhere Modellgenauigkeiten.
Darüber hinaus ist das Verständnis der inneren Mechanismen von Layer Normalization auch hilfreich bei der Fehlersuche und beim Debugging von Trainingsprozessen. Abweichungen im Gradientenfluss, welche die Trainingsdynamik negativ beeinflussen, können so gezielter lokalisiert und behoben werden. Abschließend ist Layer Normalization eine unverzichtbare Methode in der modernen Deep-Learning-Praxis. Die Berechnung der Gradienten im Backward Pass, besonders der komplexe Teil der Ableitung nach den Eingaben xj, bildet das Fundament für eine erfolgreiche Trainingsoptimierung. Durch detaillierte mathematische Herleitungen und präzise Formeln kann der Anwender verstehen, wie die verschiedenen Komponenten der Normalisierung zusammenwirken und wie sie in der Praxis effizient umgesetzt werden.
Wer sich mit Layer Normalization und ihrer Implementierung intensiv auseinandersetzt, gewinnt dadurch entscheidende Vorteile für das Design anspruchsvoller und leistungsfähiger neuronaler Modelle in vielfältigen Einsatzgebieten.