In den letzten Jahren haben neuronale Netzwerke die Welt der künstlichen Intelligenz maßgeblich geprägt, insbesondere im Bereich der Bildverarbeitung und Mustererkennung. Trotz beeindruckender Erfolge bleibt jedoch die Funktionsweise tiefer neuronaler Netzwerke oft undurchsichtig. Warum schaffen es diese Netzwerke, komplexe Klassifikationsaufgaben zu lösen, und welche Grenzen existieren dabei? Um diese Fragen zu verstehen, lohnt es sich, neuronale Netzwerke aus einer mathematischen Perspektive zu betrachten, insbesondere im Zusammenhang mit mannigfaltigen Strukturen und der Topologie. Neuronale Netzwerke transformieren Eingabedaten durch zahlreiche Schichten auf eine Art und Weise, die es ermöglicht, unterschiedliche Klassen mittels linearer Trennung voneinander zu unterscheiden. Diese Transformationen können als Abbildungen betrachtet werden, die den Raum der Eingabedaten kontinuierlich verzerren, ohne ihn zu zerreißen oder zu schneiden.
Hier kommt die Topologie ins Spiel: Sie untersucht genau solche Eigenschaften von Räumen, die durch stetige Transformationen erhalten bleiben. Eines der zentralen Konzepte hierbei ist die Idee der Mannigfaltigkeiten. Ein manifold ist ein Raum, der lokal wie ein euklidischer Raum aussieht, aber global komplexere Strukturen annehmen kann. Natürliche Daten, etwa Bilddaten, werden oft angenommen, sich auf solchen niederdimensionalen Mannigfaltigkeiten im hochdimensionalen Eingaberaum zu befinden. Diese Annahme wird als Mannigfaltigkeits-Hypothese bezeichnet und liefert eine Erklärung dafür, warum neuronale Netzwerke trotz der enormen Datenkomplexität gut generalisieren können.
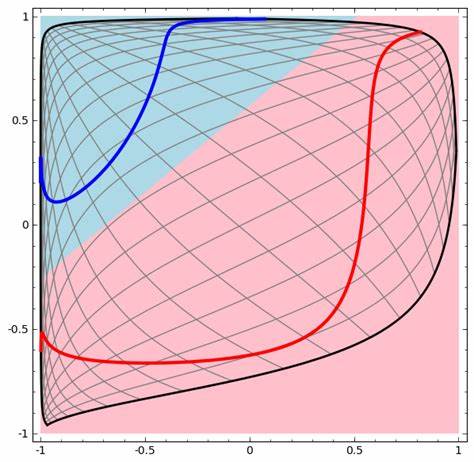
Das Verständnis der Topologie der Daten ist deshalb nicht nur ein theoretisches Unterfangen, sondern hat praktische Konsequenzen für die Auslegung und Leistungsfähigkeit von neuronalen Netzwerken. Beispielsweise gibt es Situationen, in denen sich zwei Klassen in der Eingabedatenmenge so verknäuelt oder verschlungen darstellen, dass einfache Netzwerke mit wenigen Neuronen unmöglich eine klare Trennung erzielen können. In solchen Fällen ist es mathematisch nachweisbar, dass eine Mindestanzahl von Neuronen erforderlich ist, um die Klassen in einer höherdimensionalen Repräsentation voneinander trennen zu können. Ein anschauliches Beispiel hierfür sind zwei von einander umschlungene Kurven oder Spiralen im zweidimensionalen Raum. Ein einfaches neuronales Netzwerk mit wenigen verborgenen Einheiten ist nicht in der Lage, diese zu trennen, da jede Schicht des Netzwerks topologische Eigenschaften erhält.
Ein Netzwerk, das nur aus schichten mit zwei Neuronen besteht, kann die topologische Struktur der umschlungenen Klassen nicht entsprechend verändern, was den Erfolg bei der Klassifikation verhindert. Interessant ist, dass jede Schicht aus einer linearen Transformation gefolgt von einer nichtlinearen, stetigen und monotonen Aktivierungsfunktion wie der Tangens-Hyperbolicus-Funktion (tanh) besteht. Diese Schichten sind sogenannte Homöomorphismen, was bedeutet, dass sie topologische Eigenschaften unverändert lassen. Die Daten werden zwar verzerrt, gespreizt oder zusammengedrückt, aber nicht zerschnitten oder gefaltet. Dadurch entsteht eine Abbildung, die stetig und invertierbar ist, solange die Gewichtematrix nicht singulär ist.
Diese Tatsache lässt sich nutzen, um die Funktionsweise von neuronalen Netzwerken durch sogenannte kontinuierliche Visualisierungen zu beobachten. Dabei wird visualisiert, wie sich die Darstellung eines Datensatzes im geometrischen Raum von Schicht zu Schicht verändert, bis eine lineare Trennung durch eine Hyperbene möglich wird. Erste Entwicklungen dieser Visualisierung ermöglichen ein intuitives Verständnis darüber, wie tiefere Schichten komplexe Datenstrukturen entwirren und vereinfachen. Die Topologie bietet auch einen Rahmen, um schwierige Konzepte innerhalb des maschinellen Lernens wie das vernetzte oder geknotete Verknüpfen von Datenmodellen zu durchdringen. Beispielsweise können Datensätze, die man sich als zwei miteinander verbundene Tori, also Donut-förmige Mannigfaltigkeiten, vorstellen kann, eine Klassifikation nur dann zulassen, wenn der Netzwerkraum in eine ausreichend hohe Dimension erweitert wird.
Damit werden Verknüpfungen im Datenraum sichtbar und entwirrbar. Dieser Zusammenhang zwischen Knotentheorie und neuronalen Netzwerken eröffnet spannende Perspektiven, da er nahelegt, dass manche Klassifikationsprobleme mit einem zu flachen oder engen Netzwerk prinzipiell nicht lösbar sind. Das bedeutet, dass nicht allein die Tiefe eines Netzes entscheidend ist, sondern auch die Dimension seiner verborgenen Schichten eine fundamentale Rolle spielt, um die topologische Komplexität der Daten zu bewältigen. Im Kontext moderner Anwendungen wie der Bildklassifikation und natürlicher Sprachverarbeitung bringt dies eine neue Perspektive in die Gestaltung von Netzarchitekturen. Klassische neuronale Schichten, die affine Transformationen mit punktweisen Aktivierungsfunktionen kombinieren, sind limitiert in ihrer Fähigkeit, topologische Verwicklungen zu lösen.
Daher gewinnen neue Schichttypen an Bedeutung, die darauf ausgelegt sind, Mannigfaltigkeiten gezielter zu manipulieren, etwa durch das Erlernen von Vektorfeldern, welche die Daten kontinuierlich verschieben und entwirren. Ein alternativer Ansatz zur klassischen linearen Klassifikation ist die Nutzung von k-Nearest-Neighbor (k-NN) Algorithmen, die stark von einer guten Datenrepräsentation abhängen. Mittels neuronaler Netze kann man lernen, geeignete Repräsentationen zu erstellen, auf denen k-NN effizient arbeitet und so die Trennung der Klassen verbessert wird. Dadurch wird der Fokus vom streng linearen Trennen hin zur Anordnung der Datenpunkte in einem Raum verlagert, in dem Punkte derselben Klasse näher beieinander liegen und Punkte unterschiedlicher Klassen weiter entfernt. Trotz der vielversprechenden theoretischen Grundlagen bleiben Herausforderungen in der Praxis bestehen.
Lokale Minima im Optimierungsprozess können dazu führen, dass Modelle suboptimale Lösungen finden, etwa wenn sie versuchen, die Mannigfaltigkeiten lediglich lokal zu strecken, anstatt sie global sinnvoll zu entwirren. Die Anwendung von kontraktiven Regularisierungen und weiteren Techniken zielt darauf ab, solche Fehler zu reduzieren und robustere Netzwerke zu erzielen. Aus topologischer Sicht nötigen Klassenverteilungen neuronale Netzwerke dazu, mit höherdimensionalen Darstellungen zu arbeiten, um Variationen, Verknüpfungen und komplexe Formen zu erfassen. Darin liegt eine tiefe Verbindung zwischen abstrakter Mathematik und praktischen Algorithmen des maschinellen Lernens. Das Erkennen und Ausnutzen dieser Verbindung verspricht nicht nur ein besseres Verständnis bestehender Modelle, sondern auch die Entwicklung neuartiger Architekturen und Verfahren.
Insgesamt zeigt sich, dass das Zusammenspiel von neuronalen Netzwerken, Mannigfaltigkeiten und Topologie eine faszinierende Schnittstelle ist, die sowohl theoretisch als auch praktisch von großer Bedeutung ist. Sie eröffnet Wege, die Grenzen heutiger Technologien zu überwinden und bilden eine Brücke zwischen reiner Mathematik und angewandter Informatik. Neue Forschungsansätze, die diese Perspektiven vertiefen, können das Potenzial neuronaler Netzwerke und KI-Systeme in vielen Anwendungsgebieten weiter entfesseln.