Der schnellste Weg zum Färben von Graphen: Revolutionäre Algorithmen verändern die Graphentheorie

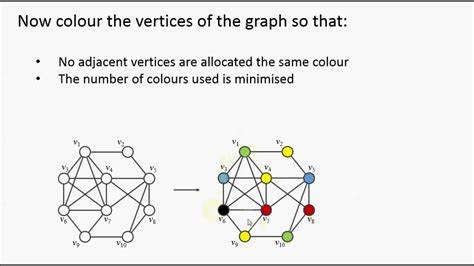
Graphentheorie ist ein zentrales Forschungsgebiet in Mathematik und Informatik, das sowohl theoretische als auch praktische Bedeutung hat. Eine der herausforderndsten Aufgaben ist das Färben von Graphen, bei der den Kanten eines Graphen Farben zugewiesen werden, sodass keine zwei Kanten, die an einem gemeinsamen Punkt anliegen, die gleiche Farbe erhalten. Diese Constraint ist nicht nur eine abstrakte mathematische Übung, sondern hat wichtige Anwendungen in Bereichen wie Luftverkehrskontrolle, Netzwerksicherheit und Ressourcenmanagement. Bis vor kurzem galten Algorithmen zum Färben von Graphen als relativ langsam und konnten trotz intensiver Forschung seit Jahrzehnten kaum verbessert werden. Doch seit 2024 hat sich die Situation dramatisch verändert, als Forscher neue Techniken entwickelten, die das Problem mit nahezu optimaler Geschwindigkeit lösen – eine Revolution, die weit über die Grenzen reiner Theorie hinausgeht.

Um die Bedeutung dieses Durchbruchs zu verstehen, lohnt es sich, mit einem realen Beispiel zu beginnen: die Koordination des Bodenverkehrs am Flughafen Newark nahe New York. Die Herausforderung besteht darin, Flugzeuge so über Start- und Landebahnen, Taxiwege und zu ihren Gates zu leiten, dass es keine Kollisionen gibt. Modelliert man jeden wichtigen Punkt am Flughafen als Knoten eines Graphen und jede Strecke, die ein Flugzeug zurücklegen muss, als Kante zwischen diesen Knoten, entsteht ein komplexes Netzwerk. Das Ziel ist es, die einzelnen Kanten mit verschiedenen Farben zu versehen, wobei jede Farbe eine bestimmte Zeitperiode symbolisiert. Durch die Farbzuweisung wird sichergestellt, dass nie zwei Flugzeuge denselben Knoten zur gleichen Zeit nutzen und somit Kollisionen vermieden werden können.

Die Herausforderung besteht darin, all diese Kanten schnell mit Farben zu versehen, selbst wenn dieser Graph aus Milliarden von Verbindungen besteht. Die klassischen Algorithmen, die seit den 1960er-Jahren verwendet werden, waren zwar korrekt, aber langsam und bei riesigen Graphen praktisch unbrauchbar. Hier setzt die neue Generation von Algorithmen an, die seit 2024 entwickelt wurden und einen Paradigmenwechsel darstellen. Ein Meilenstein der Graphentheorie war das Theorem von Vadim Vizing aus dem Jahr 1964. Er bewies, dass man zur minimalen Färbung einer Graphkante maximal um eins mehr Farben benötigt als die größte Anzahl von Kanten, die an einem Punkt zusammenlaufen.

Obwohl dieses Ergebnis elegant und fundamental ist, war Vizings eigener Algorithmus zum tatsächlichen Färben sehr langsam, mit einer Laufzeit proportional zum Produkt aus der Anzahl der Kanten m und der Anzahl der Knoten n im Graphen. In den folgenden Jahrzehnten wurden die Algorithmen zwar verbessert, die Fortschritte waren jedoch allmählich und erreichten nur bis zu einer Laufzeit proportional zu m mal der Quadratwurzel von n. Dieser Umstand erzeugte eine Art Stillstand in der Forschung, da neue Ideen fehlten, um die Geschwindigkeit signifikant zu erhöhen. Viele Versuche, das altbekannte Problem schneller zu lösen, blieben erfolglos, bis die Forschungslandschaft 2024 von einem plötzlichen Innovationsschub geprägt wurde. Sepehr Assadi von der University of Waterloo sowie parallele Forschungsteams präsentierten Ergebnisse, die das Problem grundlegend beschleunigten.

Assadi erreichte eine Laufzeit von ungefähr n², während andere Teams den Wert auf m mal der dritten bzw. vierten Wurzel von n reduzieren konnten. Diese Revolution wurde durch den Einsatz neuartiger Techniken ermöglicht, insbesondere durch die geschickte Integration von Zufallsverfahren, die bisher kaum genutzt wurden. Der entscheidende Paradigmenwechsel bestand darin, sich nicht länger darauf zu konzentrieren, eine einzelne Kante besonders schnell zu färben, sondern mehrere Kanten nahezu gleichzeitig zu bearbeiten. Diese strategische Wende ermöglichte es, die Zeitkomplexität näher an die theoretische Untergrenze zu bringen: den linearen Aufwand in Bezug auf die Anzahl der Kanten m.

Denn selbstverständlich kann ein Algorithmus niemals schneller sein, als die Zeit, die benötigt wird, um alle Kanten überhaupt einmal zu betrachten. Die Forscher übernahmen daher die Idee eines „Vorstrichs“ aus der Malerwelt. In der Praxis verwendet man vor dem endgültigen Farbauftrag einen Grundierungsanstrich, um die Oberfläche gleichmäßig vorzubereiten und spätere Arbeitsgänge zu erleichtern. Analog dazu „grundierten“ sie den Graphen mit einer zufallsbasierten Methode, die den Großteil der Kanten nach einem Zufallsschema vorfärbte. Dadurch blieben nur bestimmte komplexe Stellen unberührt, die anschließend viel einfacher und oft parallel bearbeitet werden konnten.

Dieses Verfahren kombiniert Eleganz und mathematische Tiefe und führte zu Algorithmen mit Laufzeiten, die nur noch proportionale Größenordnungen zu m mal dem Logarithmus von m haben – praktisch eine lineare Zeit. Derartige Fortschritte wurden von Größen der Informatik begeistert aufgenommen. Robert Tarjan, Turing-Preisträger und Professor an der Princeton University, bezeichnete die neue Strategie als bahnbrechend. Sie wecke neue Hoffnungen auf eine Lösung eines Problems, das fast sechzig Jahre lang als festgefahren galt. Es ist ein klassisches Beispiel dafür, wie frische Perspektiven und interdisziplinäre Inspiration reale Paradigmen eines Forschungsfelds verändern können.

Dennoch bleiben noch offene Fragen: Die letzten Optimierungen enthalten nach wie vor logarithmische Faktoren in der Laufzeit, was bedeutet, dass sie knapp oberhalb einer perfekten linearen Zeit liegen. Die Forscher sind bestrebt, diese Faktoren vollständig zu eliminieren, was theoretisch möglich, aber bislang technisch extrem herausfordernd ist. Darüber hinaus wäre es wünschenswert, den Einsatz von Zufallselementen zu vermeiden, um Algorithmen mit garantierter Laufzeit unter allen Umständen zu erhalten. Das schließe auch deterministische Methoden ein, die unabhängig von Glück oder Zufall stets konstant schnell arbeiten. Diese Fragen sind nicht nur akademischer Natur, sondern haben konkrete praktische Auswirkungen.

In realen Anwendungen wie Netzwerkverwaltung, Telekommunikation, Scheduling und Verkehrssteuerung sind Algorithmen gefragt, die nicht nur schnell im asymptotischen Sinne sind, sondern auch stabil, vorhersehbar und effizient bei großen Datenmengen operieren. Daher ist es wichtig, dass die theoretischen Fortschritte in der Algorithmendynamik auch in praxistaugliche Software übertragen werden. Die enorme Bedeutung dieser neuen Algorithmen liegt auch im Potenzial, zahlreiche Probleme in der Informatik effizienter zu lösen. Graphfärbung ist eng verwandt mit vielen anderen Aufgaben wie Matching-Algorithmen, Ressourcenzuweisung und Netzwerkoptimierung. Fortschritte in der Grundtechnik können daher eine ganze Reihe von Anwendungen beschleunigen und neue Forschungsfelder eröffnen.

Ein weiterer interessanter Aspekt ist die Interdisziplinarität, die bei der Erarbeitung dieser Methoden eine Rolle spielt. Die Kombination von Zufallsprozessen, graphentheoretischem Wissen und algorithmischer Effizienz verdeutlicht, wie moderne Forschung oft an der Schnittstelle verschiedener Disziplinen angesiedelt ist. Diese Vielfalt der Ansätze fördert Innovationen und schafft Lösungen, die sich nicht auf ein isoliertes Fachgebiet beschränken. Zusammengefasst markiert der aktuelle Durchbruch im Färben von Graphen eine Ära der nahezu optimalen Algorithmen, die theoretische Grenzen erreichen und damit eine Vielzahl von Anwendungen transformieren können. Während weiterhin Herausforderungen bestehen, ist der Weg für praktische und schnelle Lösungen geebnet, die in Zukunft ein fester Bestandteil moderner Computerwissenschaften und angewandter Mathematik sein werden.

Insgesamt wird klar, dass der Fortschritt im Graphfärbeproblem weit mehr ist als eine mathematische Kuriosität. Er zeigt, wie tief verwurzelte Herausforderungen mit Kreativität, Kollaboration und dem Mut, neue Wege zu gehen, überwunden werden können. Die derzeitigen Spitzenalgorithmen sind somit ein Meilenstein, der das Feld der Graphentheorie neu definiert, und eröffnen faszinierende Perspektiven für Wissenschaft und Technik.