Rekursion stellt in der Programmierung ein mächtiges Konzept dar, das besonders in JavaScript aufgrund seiner Flexibilität und Ausdrucksstärke eine zentrale Rolle spielt. Dabei ruft eine Funktion sich selbst auf, um ein Problem Schritt für Schritt zu lösen. Die Verwendung von Rekursion ermöglicht es, Aufgaben zu bewältigen, die mit normalen Schleifen oder iterativen Ansätzen schwer oder unübersichtlich wären. Neben mathematischen Problemen, wie der Berechnung von Fakultäten oder der Fibonacci-Folge, ist Rekursion besonders wertvoll bei der Arbeit mit hierarchischen Datenstrukturen, beispielsweise bei der Traversierung von Bäumen oder Verschachtelungen. Auf den ersten Blick mag Rekursion komplex und schwer verständlich erscheinen, doch mit den richtigen Konzepten und praktischen Beispielen kann man dieses Werkzeug schnell meistern und effektiv nutzen.
Grundlegend lässt sich Rekursion durch zwei wesentliche Komponenten beschreiben: den Abbruchfall, damit die Funktion nicht endlos wiederholt wird, und den rekursiven Schritt, bei dem die Funktion sich selbst mit einem veränderten Parameter aufruft und somit allmählich auf den Abbruchfall zusteuert. Ein klassisches Beispiel, um das Prinzip zu verdeutlichen, ist die Berechnung der Fakultät einer Zahl. Hierbei multipliziert man eine Zahl mit der Fakultät der um eins kleineren Zahl, bis man bei der Eins angekommen ist, welche als Abbruchbedingung dient. Die Implementierung in JavaScript gestaltet sich folgendermaßen: eine Funktion nimmt eine Zahl entgegen und prüft, ob sie den Wert Eins erreicht hat. Falls ja, gibt sie Eins zurück.
Andernfalls erfolgt der rekursive Aufruf mit der um eins verminderten Zahl. Dieses Prinzip illustriert anschaulich, wie durch den rekursiven Aufruf komplexe Abläufe elegant vereinfacht werden können. Ein weiteres praktisches Beispiel ist die Berechnung der Summe über einen Zahlenbereich. Hierbei summiert eine Funktion stilistisch das obere Ende des Bereichs auf das Ergebnis eines rekursiven Aufrufs, bei dem das obere Ende um eins reduziert wird, bis dieses mit dem unteren Ende identisch ist. Die Logik sorgt dafür, dass jeder Wert einmal addiert wird, wobei die Funktion schrittweise zum Basisfall zurückkehrt.
Dieses Beispiel zeigt, wie Rekursion zur Aggregation von Werten genutzt werden kann, ohne auf iterative Schleifenkonstruktionen zurückzugreifen. Die bekannte Fibonacci-Folge demonstriert jedoch auch die Grenzen einfacher rekursiver Implementierungen. Die naive Lösung berechnet jeden Wert durch Addition der beiden vorhergehenden, wobei die Funktion sich daher mehrfach mit denselben Eingaben aufruft. Dies führt zu exponentiellen Laufzeiten und verringert die Performance erheblich. Um diesen Nachteil zu beheben, bieten sich Optimierungstechniken wie Memoisierung an.
Dabei werden Zwischenergebnisse in einem Speicher gehalten und bei Bedarf sofort zurückgegeben. Dies reduziert die Anzahl der erforderlichen Funktionsaufrufe drastisch und bringt die Laufzeit auf eine lineare Komplexität. Tail-Recursion ist eine weitere mächtige Optimierungsmöglichkeit, bei der der letzte Funktionsaufruf in einer rekursiven Funktion eine Rekursionsstelle ist, die es modernen JavaScript-Engines erlaubt, den bestehenden Stackframe wiederzuverwenden. Dadurch vermindert sich die Wahrscheinlichkeit eines Stack Overflows bei tiefen Rekursionen. Tail-Recursion verändert das Layout der Funktion leicht, indem jedwede Rechenoperation vor den rekursiven Aufruf ausgelagert wird und nur das Ergebnis weitergereicht wird.
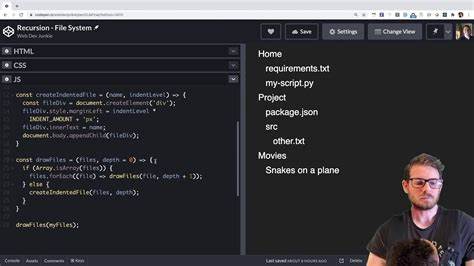
Allerdings ist die Unterstützung für Tail-Call-Optimierung in JavaScript aktuell noch nicht in allen Umgebungen einheitlich gegeben. Neben den bereits genannten mathematischen Beispielen spielt Rekursion besonders bei der Traversierung von verschachtelten Objekten und Baumstrukturen eine unschätzbare Rolle. Natürliche Baumgebilde, wie DOM-Elemente, Verzeichnisse oder hierarchische Daten, können hier mit einer kurzen rekursiven Funktion durchlaufen und bearbeitet werden. Dabei ruft die Funktion für jeden Knoten alle Kindknoten rekursiv auf, bis das Ende der Baumstruktur erreicht ist. Die Verwendung von Rekursion in solchen Szenarien sorgt für eine klare, intuitive und wartbare Lösung.
Trotz der vieler Vorteile sollte man bei der Verwendung von Rekursion auch mögliche Nachteile beachten. Zu tiefe Rekursionen können zu einem Stapelspeicherüberlauf (Stack Overflow) führen und so das Programm zum Absturz bringen. Ebenso erhöht jeder Funktionsaufruf die Laufzeit durch Aufrufkosten, was bei großen Datenmengen ohne Optimierung zu Performanceproblemen führen kann. Außerdem ist dabei stets auf klare und eindeutige Basisfälle zu achten, damit sich die Funktion nicht unendlich selbst aufruft. Wo sinnvoll, sollte man zusätzlich Optimierungen implementieren oder gegebenenfalls iterative Alternativen in Erwägung ziehen.