Faszinierende Welt der Polyeder entdecken mit dem Polyhedra Viewer

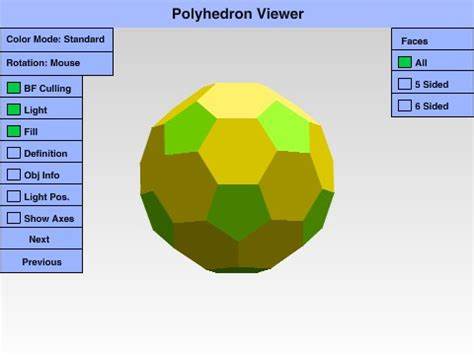
Die geometrische Form der Polyeder übt seit Jahrhunderten eine besondere Faszination auf Mathematiker, Künstler und Wissenschaftler aus. Polyeder sind dreidimensionale Körper, die von ebenen Flächen begrenzt werden. Während die meisten Menschen vielleicht mit den bekannten platonischen Körpern wie Tetraeder, Würfel oder Ikosaeder vertraut sind, verbirgt sich hinter der Welt der Polyeder eine überraschende Vielfalt an Formen, deren Eigenschaften und Verwandtschaften eine außergewöhnliche Komplexität und Schönheit aufweisen. Der Polyhedra Viewer ist eine moderne Anwendung, die genau diese Vielseitigkeit visualisiert und es ermöglicht, die Beziehungen zwischen den verschiedenen Polyederklassen auf eine intuitive Weise zu erleben und zu verstehen. Das Herzstück des Polyhedra Viewers bildet die Präsentation der 120 konvexen, regulär-gesichteten Polyeder zusammen mit ihren Verwandlungen.

Dieses Netzwerk aus Operationen erlaubt es Nutzern, die Verbindungen zwischen den einzelnen Formen nachzuvollziehen und ein tiefes Verständnis für die Struktur der Polyederwelt zu entwickeln. Dabei sind nicht nur bekannte Figuren wie die platonischen oder archimedischen Körper enthalten, sondern auch die weniger geläufigen Johnson-Soliden, deren Konstruktionen und Zusammensetzungen von besonderem Interesse sind. Die platonischen Körper gelten als die Urformen der Polyeder. Sie besitzen regelmäßig viele gleiche Flächen und sind vollkommen symmetrisch. Der Tetraeder, Würfel, Oktaeder, Dodekaeder und Ikosaeder stehen exemplarisch für diese Klasse.

Ihre mathematische Reinheit und ästhetische Anmutung machen sie sowohl in der Kunst als auch in der Wissenschaft zu Ikonen. Der Polyhedra Viewer zeigt diese Formen nicht isoliert, sondern auch in ihren abgewandelten Gestalten, etwa in Form von Trunkierungen, Rektifizierungen oder Snub-Varianten, die durch den Einsatz bestimmter geometrischer Operationen entstehen. Neben den platonischen Körpern umfasst der Viewer auch die archimedischen Polyeder, die sich durch regelmäßige Flächen, aber variierende Flächentypen auszeichnen. Diese erweitern das Spektrum der Formen signifikant und demonstrieren, wie aus Symmetrie, Klarheit und Variation neue ästhetische Formen entstehen können. Ebenso werden die unendlichen Reihen von Prismata und Antiprisma dargestellt, die als Grundbausteine und Übergangsformen fungieren und deren praktische und theoretische Bedeutung innerhalb der Polyederwelt kaum zu überschätzen ist.

Ein besonderer Abschnitt des Polyhedra Viewers widmet sich den Johnson-Soliden, die nach Norman Johnson benannt sind. Diese 92 Polyeder besitzen reguläre Flächen, jedoch fehlt ihnen die vollständige symmetrische Äquivalenz der Ecken. Dadurch zeichnen sie sich durch eine gewisse Unregelmäßigkeit aus, die ihnen aber keineswegs ihre Anziehungs- und Forschungsenergie nimmt – im Gegenteil. Viele davon entstehen durch Kombinationen von Pyramiden, Cupolæ und Rotundæ mit Prismen und Antiprisma, was ihre komplexe und faszinierende Entstehungsgeschichte zeigt. Der Viewer erlaubt es, auch diese besonderen Formen detailliert zu betrachten und in die verschiedenen Kategorien, wie etwa ortho-, gyro- oder bi-elonierte Solide, einzutauchen.

Darüber hinaus bietet die Anwendung einen Einblick in augmentierte, diminuierte und gyrate Polyeder. Diese entstehen durch gezielte Veränderungen an bereits existierenden Formen, wobei Teile hinzugefügt oder entfernt und so neue Varianten geschaffen werden. Diese Prozesse zeugen von der immensen Vielfalt der Welt der Polyeder und spiegeln gleichzeitig eine künstlerische Herangehensweise wider, die aus Mathematik und Design schöpft. Ein weiterer Höhepunkt im Polyhedra Viewer ist die Möglichkeit, mittels einer interaktiven Oberfläche die Polyeder zu manipulieren. Nutzer können Formen auswählen, drehen, verkleinern oder vergrößern und so selbst die Verschmelzungen und Divergenzen von einzelnen Polyedern nachvollziehen.

Diese direkte Visualisierung macht komplexe mathematische Konzepte greifbar und kann sowohl für interessierte Laien als auch für Experten in den Bereichen Mathematik, Architektur, Design oder Kunst von großem Nutzen sein. Über die Darstellung der konvexen und regulären Polyeder hinaus lädt der Polyhedra Viewer auch dazu ein, die rein ästhetische und konzeptuelle Dimension der Polyederwelt zu erforschen. Von den Kepler-Poinsot-Körpern, die zwar regulär aber nicht konvex sind, bis hin zu den Catalanischen Körpern, die als Duale der archimedischen Solide gelten und unregelmäßige Flächen besitzen, bietet sich ein reichhaltiger Fundus an Formen, der weit über die Grundtypen hinausgeht. Selbst mehrdimensionale Erweiterungen, wie der vierdimensionale Tesserakt oder das grand antiprism, werden in seinem erweiterten Kontext diskutiert und eröffnen faszinierende Perspektiven auf Geometrie jenseits unseres dreidimensionalen Raumes. Für alle, die tiefer in die polyedrische Welt eintauchen wollen, bietet der Polyhedra Viewer Links zu weiterführenden Ressourcen, die auf umfangreichen Datenbanken und Forschungsprojekten basieren.

So stammen viele Inspirationen und die zugrundeliegenden geometrischen Daten etwa von George W. Hart, dessen «Virtual Polyhedra» eine der umfangreichsten Sammlungen an Polyederwissen darstellt. Auch Visualisierungen von David I. McCooey und Anselm Levskaya werden verlinkt, wodurch Nutzer Zugang zu noch detaillierteren Modellen und Konstruktionsprinzipien erhalten. Die Integration von Conway-Operationen, welche spezielle geometrische Transformationen ermöglichen, erlaubt es, durch einfache Schritte komplexe neue Polyederformen zu erschaffen.

Dies stellt eine Brücke zwischen der exakten Mathematik und der kreativen Gestaltung dar. Ebenso bietet die Seite von Stacy Speyer künstlerisch inspirierte Modelle an, was zeigt, dass Polyeder keineswegs nur trocken-mathematische Objekte sind, sondern auch lebendige Formen der Kunst und des Designs darstellen. Ein besonderes Merkmal des Polyhedra Viewers ist die moderne technische Umsetzung. Die Seite wurde mit React und X3DOM aufgebaut, was die interaktive 3D-Darstellung in Echtzeit ermöglicht und so ein sehr fließendes Nutzererlebnis schafft. Die Benutzerfreundlichkeit und der intuitive Zugriff auf komplexe Daten machen den Viewer zu einem wertvollen Werkzeug für Bildung und Forschung.

Dabei ist auch die Integration sozialer Funktionen, wie das Teilen auf Facebook, Twitter und Reddit, ein wichtiges Element, um das Interesse an Polyedern und geometrischen Formen zu fördern und eine Community von Gleichgesinnten zu bilden. Der Reichtum der polyedrischen Formen, ihre Verwandtschaften und Transformationen, die durch den Polyhedra Viewer anschaulich gemacht werden, öffnen spannende Anwendungsmöglichkeiten. In der Architektur etwa dienen Grundprinzipien der Polyeder als Grundlage für modulare Strukturen, Kuppeln oder innovative Designobjekte. In der Chemie und Materialwissenschaft helfen Polyeder bei der Modellierung von Molekülstrukturen und Kristallgittern. Selbst in der Computergrafik und Spielentwicklung sind polyedrische Modelle von großer Bedeutung für die Gestaltung von virtuellen Welten.

Für alle, die sich für Mathematik, Geometrie, Kunst oder Design interessieren, eröffnet sich mit dem Polyhedra Viewer eine faszinierende Welt, die zum Entdecken, Verstehen und Gestalten einlädt. Die Kombination aus didaktisch sinnvoller Aufbereitung, wissenschaftlicher Genauigkeit und künstlerischem Anspruch macht das Werkzeug einzigartig. Es unterstützt nicht nur das Lernen, sondern inspiriert dazu, die Formen in neuen Kontexten zu sehen und kreativ zu nutzen. Wer sich auf eine Reise durch die vielfältigen Ebenen der Polyederwelt begeben möchte, findet mit dem Polyhedra Viewer einen verlässlichen und inspirierenden Begleiter. Die Möglichkeit, Formen zu visualisieren, zu manipulieren und deren Beziehungen nachzuvollziehen, fördert das Verständnis für komplexe geometrische Zusammenhänge und vermittelt zugleich die zeitlose Schönheit dieser faszinierenden Körper.

Die stetig wachsende digitale Plattform, verbunden mit wissenschaftlicher Expertise und künstlerischem Gestaltungswillen, sichert dem Thema auch in Zukunft eine herausragende Position im Bereich der Bildung und Forschung. Schlussendlich zeigt der Polyhedra Viewer, dass die Welt der Polyeder weit mehr ist als nur eine Sammlung von geometrischen Figuren. Es ist ein lebendiges Universum aus Formen, Transformationen und Prinzipien, das nicht nur mathematisch fundiert, sondern auch visuell und ästhetisch ansprechend ist. Wer sich darauf einlässt, wird mit neuen Perspektiven und einem tiefen Verständnis für die Struktur, Schönheit und Vielfalt geometrischer Körper belohnt.