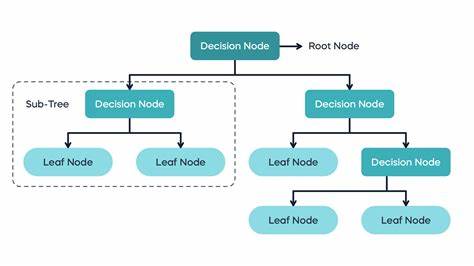
Entscheidungsbäume zählen zu den beliebtesten Methoden im Bereich des maschinellen Lernens, nicht zuletzt wegen ihrer intuitiven Interpretierbarkeit und breiten Anwendbarkeit bei Klassifikations- und Regressionsproblemen. Die Implementierung solcher Bäume, insbesondere der sogenannten CART-Algorithmen (Classification and Regression Trees), erfordert ein tiefgehendes Verständnis der zugrundeliegenden Konzepte sowie der mathematischen und algorithmischen Herausforderungen, die mit der Baumerstellung einhergehen. Ein zentrales Ziel bei der Implementierung ist es dabei, effiziente Modelle zu schaffen, die auch auf größeren Datensätzen ohne exponentiellen Rechenaufwand trainiert werden können.Zu Beginn der Entwicklung eines Entscheidungsbaums ist die Definition der grundlegenden Datenstrukturen unerlässlich. Hierbei wird zwischen Knoten unterteilt: Blattknoten, die eine Vorhersage speichern, und innere Knoten, welche basierend auf bestimmten Merkmalen eine Entscheidung treffen, um die Daten in zwei Teilmengen zu zerlegen.
Blattknoten speichern beispielsweise bei Klassifikationsproblemen Wahrscheinlichkeitsvektoren, während sie bei Regressionsproblemen konstante Werte, meist Mittelwerte der Zielvariable, halten. Innere Knoten hingegen benötigen Informationen zum Index des verwendeten Merkmals, dem Aufteilungswert und Referenzen zu den linken und rechten Kindknoten. Die Art des Split-Werts kann numerisch oder in Form einer Menge (für kategoriale Merkmale) vorliegen.Das Herzstück der Baumkonstruktion liegt in der Auswahl geeigneter Splits, die die Reinheit der resultierenden Knoten maximieren. Unterschiedliche Kriterien wie Gini-Impurität, Entropie oder der quadratische Verlust kommen hierbei zum Einsatz.
Diese Maße bewerten, wie homogen die Zielwerte innerhalb eines Knotens sind. Für Klassifikationsbäume wird dazu häufig die Verteilung der Klassen über Wahrscheinlichkeiten geschätzt, wobei beispielsweise die Entropie auch numerische Stabilität berücksichtigen muss, etwa indem Wahrscheinlichkeiten von Null bei der Berechnung ignoriert werden. Für Regression hingegen kommt meist der quadratische Verlust zum Tragen, der auf der Varianz der Zielwerte in den Teilmengen basiert.Die Herausforderung besteht darin, für jede mögliche Aufteilung aller Merkmale diejenige zu finden, welche den Informationsgewinn maximiert oder die Unreinheit minimiert. Der naive Ansatz, alle möglichen Teilungen auszuprobieren und für jede die Kriterien neu zu berechnen, führt allerdings zu einer Zeitkomplexität von O(D N² log N), wobei D die Anzahl der Merkmale und N die Anzahl der Datenpunkte ist.
Dies wird schnell unpraktikabel, insbesondere bei großen Datensätzen. Durch geschickte Beobachtungen lässt sich dieser Aufwand reduzieren, zum Beispiel indem man sukzessive nur jeweils einen Datenpunkt von einer Seite zur anderen verschiebt und dabei die Kriterien in konstanter Zeit aktualisiert. So sinkt die Komplexität auf etwa O(D N log N).Auch Stichprobengewichte werden bei der Implementierung berücksichtigt. Diese geben nicht jedem Datenpunkt den gleichen Einfluss bei der Aufteilung.
Gewichtete Datensätze können beispielsweise bei unbalancierten Klassen oder bei Ensemble-Methoden wie Boosting zum Tragen kommen. Das Ermitteln von Wahrscheinlichkeiten und Knotenwerten erfolgt dann gewichtet, was zu präziseren oder spezielleren Bäumen führen kann.Eine besondere Schwierigkeit stellen kategoriale Merkmale dar. Klassisch behandeln viele Implementierungen diese, indem sie sie mittels One-Hot-Encoding in numerische Merkmale umwandeln. Dies kann allerdings die Anzahl der Merkmale stark erhöhen und die Trainingszeit verlängern.
Eine Alternative ist die sogenannte One-vs-Rest-Strategie beim Splitten, bei der jeder Wert eines kategorialen Merkmals einzeln als Teilmenge gegen die übrigen getestet wird. So werden nicht alle möglichen Teilmengen durchprobiert, deren Anzahl exponentiell mit der Anzahl der Kategorien ansteigen würde. Für univariate Ausgänge (etwa binäre Klassifikation oder univariatem Regression) gibt es zudem eine Optimierung basierend auf der Sortierung der Kategorien nach deren durchschnittlichem Zielwert. Diese Idee stammt aus einem klassischen statistischen Verfahren von Fisher und sorgt dafür, dass nur zusammenhängende Partitionen betrachtet werden müssen, was signifikant Zeit spart.Die rekursive Baumkonstruktion beginnt stets mit einer Wurzel, die alle Trainingsdaten umfasst, und splittet dann schrittweise weiter, solange Kriterien wie minimale Blattgröße, maximale Baumtiefe oder minimale Reduzierung der Unreinheit erfüllt sind.
Ist ein Knoten rein (beispielsweise enthält er nur Daten einer Klasse) oder die Grenzen von Stichprobengröße oder Tiefe erreicht, wird ein Blatt erzeugt, das die finale Vorhersage beinhaltet.Schließlich spielt die Vorhersage eine ebenso große Rolle wie der Trainingsprozess. Das Durchlaufen des Baumes für neue Datenpunkte ist sehr effizient und in logarhythmischer Zeit bezüglich der Anzahl der Trainingspunkte möglich. Dabei wird an jedem inneren Knoten geprüft, ob der Wert eines Merkmals unter oder über dem Split-Punkt liegt oder bei kategorialen Merkmalen ob die Kategorie dem linken oder rechten Kind zugeordnet ist. Die Zuordnung erfolgt solange rekursiv bis ein Blatt erreicht wird, dessen Wert ausgegeben wird.
Bei Klassifikation kann dies eine Wahrscheinlichkeitsverteilung über die Klassen sein, woraus mit einfachen Operationen wie dem Argmax eine finale Klasse abgeleitet werden kann.Die vorgestellten Konzepte sind in der Praxis hervorragend geeignet, um eigene Implementierungen von Entscheidungsbäumen in Python umzusetzen, die nicht nur funktional sind, sondern auch ausreichend performant für kleinere bis mittlere Datensätze funktionieren. Durch die Unterstützung von Stichprobengewichten und kategorialen Merkmalen sowie der Verwendung effizienter Update-Formeln für Aufteilungskriterien gelingt es, vielerlei Varianten von Entscheidungsbäumen zu realisieren, die auch Basisfunktionen moderner Machine-Learning-Bibliotheken wie scikit-learn oder LightGBM entsprechen.Insgesamt entsteht so ein leistungsfähiges Werkzeug, das die Kraft von Entscheidungsbäumen für Klassifikations- und Regressionsaufgaben nutzbar macht. Die realistische Zeitkomplexität und der modulare Aufbau mit klar getrennten Komponenten für Knoten, Splits, Kriterien und Baumaufbau fördern zudem die Erweiterbarkeit, etwa um Ensemble-Methoden wie Random Forests oder Boosting in Folgebeiträgen zu integrieren.
Die Wahl geeigneter Kriterien und die Einbindung von kategorischen Features durch clevere Strategien sichern zudem eine breite Anwendbarkeit der Modelle auf vielfältige Datentypen und Problemstellungen. Ein tieferes Verständnis dieser Mechanismen befähigt Entwickler und Data Scientists dazu, Entscheidungsbäume flexibel an ihre individuellen Anforderungen anzupassen und performant zu trainieren.