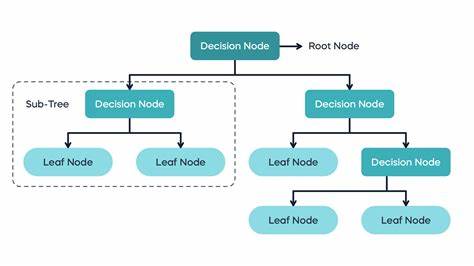
Entscheidungsbäume sind eine der grundlegendsten und gleichzeitig leistungsfähigsten Methoden im maschinellen Lernen. Sie bieten eine intuitive Möglichkeit, komplexe Entscheidungsprozesse in Form von baumartigen Strukturen darzustellen, die sowohl klassifizieren als auch regressieren können. Trotz ihrer Einfachheit weisen Entscheidungsbäume jedoch wichtige Schwächen auf: Insbesondere neigen sie zu hoher Varianz. Das bedeutet, dass kleine Veränderungen in den Trainingsdaten oft zu stark unterschiedlichen Bäumen führen, was die Verlässlichkeit der Vorhersagen einschränkt. Zudem zeigen Entscheidungsbäume eine begrenzte Flexibilität, da sie Achsen-gerichtete Splits verwenden, die nicht immer ideale Trennungen der Daten ermöglichen.
Vor diesem Hintergrund entstand die Notwendigkeit, Methoden zu entwickeln, die Entscheidungsbäume zu stabileren und leistungsfähigeren Modellen erweitern. Zwei zentrale Konzepte helfen hier weiter: Bagging – kurz für Bootstrap Aggregating – und die Random Forests, eine auf Bagging basierende Methode mit zusätzlicher Zufallskomponente bei der Merkmalsauswahl. Bagging stellt eine grundlegende Technik dar, um die Varianz von Modellen zu reduzieren. Dabei werden zahlreiche Trainingsdatensätze durch Bootstrapping, also zufälliges Ziehen mit Zurücklegen aus dem Originaldatensatz, erzeugt. Für jeden dieser Datensätze wird ein Modell – in unserem Kontext meist ein Entscheidungsbaum – trainiert.
Anschließend werden die Vorhersagen aller Modelle gemittelt, was zu einer Stabilisierung der resultierenden Schätzung führt. Theoretisch strebt man mit unendlich vielen unkorrelierten Modellen die Erwartung des optimalen Klassifikators an, da sich zufällige Fehler gegenseitig ausgleichen. In der Praxis sind unendliche Datensätze nicht verfügbar, doch Bootstrapping kommt dieser Idee nahe und lieferte empirisch überzeugende Ergebnisse. Die Besonderheit von Entscheidungsbäumen als Basis-Lernverfahren liegt darin, dass sie als instabil gelten – selbst kleine Variationen im Datensatz können die Struktur eines Baums erheblich verändern. Gerade deshalb profitieren Entscheidungsbäume besonders von Bagging, da dadurch die inhärente Varianz stark reduziert werden kann, ohne den Bias maßgeblich zu erhöhen.
Random Forests gehen über Bagging hinaus, indem sie zusätzlich bei jedem möglichen Split nur eine zufällige Teilmenge der Merkmale berücksichtigen. Diese weitere Randomisierung dient einem entscheidenden Zweck: Die einzelnen Bäume werden dadurch weniger korreliert. Ohne diese Maßnahme besteht die Gefahr, dass die durch Bagging erzeugten Bäume sich sehr ähnlich sind, da dominante Merkmale immer an erster Stelle für Splits gewählt werden. Dadurch limitiert die Korrelation zwischen Bäumen die Wirkung des Mittelns auf die Varianzreduktion. Die zufällige Merkmalsauswahl bei jedem Split zwingt jeden Baum, unterschiedliche Pfade im Entscheidungsprozess zu erkunden, wodurch die Diversität der Bäume erhöht wird.
Dieses Verfahren führt zu einer weiteren Reduktion der Vorhersagevarianz und letztlich zu verbesserten Modellergebnissen. Praktisch hat sich bewährt, für Klassifikationsprobleme eine Quadratwurzel der Gesamtanzahl der Merkmale auszuwählen, während bei Regressionsproblemen etwa ein Drittel der Gesamtmerkmale herangezogen wird. Der Bias-Varianz-Handel ist in diesem Kontext von hoher Bedeutung. Während die einzelne Baumstruktur durch Einschränkung der betrachteten Merkmale bei jedem Split eine leichte Verschlechterung der lokalen Genauigkeit erfahren kann – also einen erhöhten Bias im Modell erzeugt – führt die gleichzeitige Verringerung der Korrelation zwischen den Bäumen zu einem größeren Gewinn bei der Varianzreduktion. Im Ergebnis verbessert sich die Gesamtsystemleistung.
Gerade dieser Ausgleich macht Random Forests zu äußerst robusten und flexibel einsetzbaren Werkzeugen im maschinellen Lernen. Technisch gesehen beginnt das Training eines Random Forests, wie auch bei Bagging, mit der Erzeugung mehrerer Bootstrappedatensätze aus den Originaldaten. Für jeden dieser Datensätze wird ein Entscheidungsbaum erzeugt, bei dem in jedem Split lediglich eine zufällige Auswahl von Merkmalen zugelassen wird. Unterschiedliche Trainingsdatensätze und zufällige Merkmalswahl führen zu variierenden Baumstrukturen. Die Vorhersage eines Random Forests basiert auf dem Aggregat aller Einzelbaumvorhersagen, wobei im Falle der Klassifikation meist ein Mehrheitsvotum, beziehungsweise bei Regression der Mittelwert genommen wird.
Ein weiterer wichtiger Vorteil dieses Verfahrens ist die Möglichkeit, das sogenannte Out-of-Bag-Error (OOB-Error) abzuschätzen. Da bei der Bootstrapziehung ungefähr 37 Prozent der Originaldaten bei jedem Baum nicht als Trainingsdaten verwendet werden, dienen diese als unbeeinflusste Testbeispiele. Durch Auswertung der Vorhersagen dieser nicht ins Training einbezogenen Daten entsteht eine schlüssige Fehlerschätzung ohne die Notwendigkeit einer separaten Validierungsmenge oder eines aufwendigen Kreuzvalidierungsverfahrens. Dies erleichtert die Modellbewertung und spart Ressourcen. Random Forests weisen darüber hinaus weitere praktische Vorteile auf.
Da die Basisstruktur aus Entscheidungsbäumen besteht, sind Random Forests im Allgemeinen resistent gegenüber Ausreißern und können sowohl numerische als auch kategoriale Daten ohne spezielle Vorverarbeitung verarbeiten. Sie benötigen auch keine Normalisierung oder Skalierung der Features, was die Vorbereitung der Daten vereinfacht. Die Anzahl der Hyperparameter ist vergleichsweise gering, typischerweise beschränkt sie sich auf die Anzahl der Bäume im Wald, die maximale Tiefe der Einzelbäume, die Anzahl der Merkmale, die bei jeder Aufspaltung berücksichtigt werden, sowie Einstellungen wie Mindestanzahl von Beobachtungen in einem Blattknoten. Dadurch sind Random Forests relativ einfach zu konfigurieren und liefern selbst ohne aufwändiges Hyperparameter-Tuning solide Ergebnisse. Nichtsdestotrotz besitzen Random Forests, wie jede Methode, auch Nachteile.
Weil sie zahlreiche Einzelbäume generieren, können die Trainingszeiten und Speicheranforderungen insbesondere bei großen Datensätzen recht hoch sein. Allerdings lässt sich die Berechnung durch die Unabhängigkeit der Einzelbäume sehr gut parallelisieren, was moderne Mehrkern- und Clusterumgebungen effizient nutzen. In puncto Interpretierbarkeit büßen Random Forests gegenüber einzelnen Entscheidungsbäumen ein: Die einfache Visualisierung eines Baumes ist aufgrund der Vielzahl von Bäumen nicht mehr praktikabel. Dennoch existieren Verfahren, wie etwa die Analyse der Merkmalswichtigkeit, um zumindest Einsicht in die maßgeblichen Einflussfaktoren zu gewinnen. Aus angewandter Perspektive hat sich die Kombination aus Bagging und Random Forests als effektive Methode etabliert, um Modelle mit geringerer Varianz und gleichzeitig niedrigem Bias zu erstellen.
In vielen realen Anwendungsfällen – von der medizinischen Diagnostik über Finanzprognosen bis hin zur Bild- und Textklassifikation – liefern Random Forests robuste und zuverlässige Vorhersagen. Sie bieten einen guten Einstiegspunkt und solide Benchmark-Ergebnisse, gerade auch bei strukturierten tabellarischen Daten. Die theoretischen Grundlagen von Bagging und Random Forests wurzeln in der Statistik und Lerntheorie. Der entscheidende Vorteil ergibt sich aus der Tatsache, dass das arithmetische Mittel unabhängiger Zufallsvariablen deren Varianz verringert. Da die Einzelbäume mit Bootstrapping und Feature-Unterstichproben diversifiziert werden, sind sie nicht vollkommen korreliert, was den Varianzabfall ermöglicht.
Dennoch bleibt eine gewisse positive Korrelation zwischen den Bäumen bestehen und bestimmt letztlich das Ausmaß der Varianzreduktion. In der Praxis ist es daher wichtig, die Hyperparameter so zu wählen, dass eine gute Balance zwischen Varianz- und Biasreduktion erzielt wird. Ein weiteres Merkmal von Random Forests ist ihre Resistenz gegen Überanpassung mit zunehmender Baumanzahl. Im Gegensatz zu einzelnen Bäumen wächst mit wachsender Baumanzahl nicht die Gefahr der Überanpassung. Vielmehr stabilisiert sich das Ensemble, da durch Mittelung die zufälligen Schwankungen einzelner Bäume minimiert werden.
Das bedeutet aber nicht, dass die Wahl anderer Hyperparameter wie maximaler Baumtiefe oder Minimalgröße der Blätter keine Rolle spielt. Gerade hier kann eine zu starke Komplexität der einzelnen Bäume zu erhöhter Varianz führen, die durch Bagging nicht vollständig kompensiert werden kann. Im Vergleich zu Boosting, einer weiteren populären Ensemble-Technik, sind Random Forests leichter einzusetzen und weniger anfällig für das Überanpassen an Trainingdaten. Boosting fokussiert sich stärker auf schwer zu klassifizierende Beispiele und bindet Modelle sequenziell ein, was häufig zu höherer Genauigkeit führen kann, dabei aber komplexer in der Parametereinstellung und Berechnung ist. Random Forests sind daher besonders attraktiv, wenn eine starke, robuste Lösung mit minimalem Tuningbedarf gewünscht wird.
In der praktischen Implementierung zeigt sich, dass moderne Bibliotheken wie scikit-learn in Python, caret in R oder andere Frameworks effiziente und benutzerfreundliche Werkzeuge für Random Forests bereitstellen. Sie bieten darüber hinaus Hilfsmittel zur Visualisierung, Evaluierung, Feature-Importance-Bestimmung und zur automatischen Optimierung der Parameter. Eigene Implementierungen erfordern ein Verständnis der einzelnen Komponenten – etwa des Bootstrappings, der Baumkonstruktion und der Zufallsauswahl von Merkmalen – sind aber sehr lehrreich und helfen, das Verhalten der Algorithmen besser zu verstehen. Zusammenfassend lässt sich sagen, dass die Entwicklung von Bagging bis zu Random Forests einen wichtigen Schritt in der Evolution von Entscheidungsbäumen markiert. Sie liefern effektive Mittel, um die inhärente Instabilität einzelner Bäume auszugleichen und robustere Vorhersagemodelle zu generieren.
Die Verbindung von Bootstrap-Sampling mit zufälliger Merkmalsauswahl fördert die Diversität innerhalb des Modellensembles, was die Varianz signifikant senkt und somit die Generalisierungsfähigkeit verbessert. Aufgrund ihrer Einfachheit, Flexibilität und starken Performance bleiben Random Forests eine der meistgenutzten Methoden im maschinellen Lernen und dienen oftmals als Ausgangspunkt für weiterführende Analysen und Modellierungsprojekte.