Bias-Varianz-Dilemma: Das entscheidende Gleichgewicht für erfolgreiche Machine-Learning-Modelle

Das Bias-Varianz-Dilemma ist eines der fundamentalsten Konzepte im Bereich des maschinellen Lernens und der Statistik. Es beschreibt die Herausforderung, die richtige Balance zwischen der Vereinfachung eines Modells und dessen Komplexität zu finden, um eine möglichst präzise Vorhersage auf neuen, unbekannten Daten zu ermöglichen. Die Bedeutung dieses Trade-offs kann kaum überschätzt werden, da er entscheidend darüber entscheidet, wie gut ein Modell in der Praxis funktioniert. Das Dilemma entsteht durch den Zwiespalt zwischen Bias, also systematischer Verzerrung, und Varianz, der Empfindlichkeit gegenüber Schwankungen in den Trainingsdaten. Beim Aufbau eines Machine-Learning-Modells steht man meist vor der Entscheidung, wie komplex das Modell gestaltet sein soll.

Ein einfaches Modell, wie zum Beispiel eine lineare Regression, ist meist robust und leicht interpretierbar. Es imponiert durch geringe Varianz, reagiert aber möglicherweise nicht ausreichend flexibel auf komplizierte Zusammenhänge in den Daten. Diese Einschränkung im Modell führt zu einem hohen Bias, da das Modell die zugrundeliegenden Muster nicht vollständig erfassen kann und folglich Fehler macht. Im Gegensatz dazu steht ein sehr komplexes Modell, etwa ein tiefes neuronales Netz mit zahllosen Parametern oder ein stark verzweigter Entscheidungsbaum. Diese Modelle können extrem flexibel sein und nahezu beliebige Funktionen approximieren.

Allerdings sind sie häufig überempfindlich gegenüber kleinen Änderungen in den Trainingsdaten. Sie passen sich so genau an das vorliegende Trainingsset an, dass sie dessen Rauschen und Ausreißer mitlernen. Diese hohe Varianz führt dazu, dass das Modell auf neuen, unbekannten Daten schlechter abschneidet, obwohl es im Trainingsset eine nahezu perfekte Leistung erzielt. Ein einfaches anschauliches Beispiel aus dem Alltag kann das Bias-Varianz-Dilemma erläutern: Stellen Sie sich vor, Sie möchten Tiere als Hunde oder Katzen klassifizieren, basierend auf Merkmalen wie Größe und Gewicht. Ein Modell, das eine gerade Linie als Entscheidungsgrenze verwendet, trifft eine grobe Schätzung.

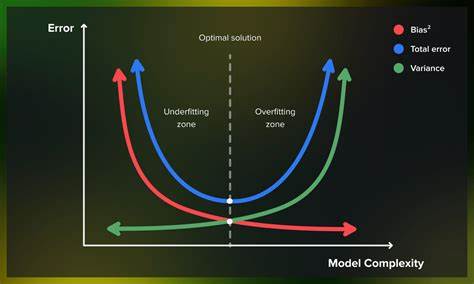
Es weist einen hohen Bias auf, weil Hunde und Katzen sich in der Realität nicht sauber linear trennen lassen. Andererseits kann ein Modell mit einer stark gewundenen Linie alle Trainingsdaten perfekt trennen, aber für neue Tiere völlig falsche Entscheidungen treffen, da es zu stark an die eigenartigen Ausprägungen der Trainingsbeispiele angepasst ist – ein Fall von hoher Varianz. Der Schlüssel zur Lösung dieses Dilemmas liegt darin, ein Modell zu entwickeln, das weder zu einfach noch zu komplex ist. Das optimale Modell navigiert geschickt zwischen der Unteranpassung – wenn es wichtige Muster übersieht – und der Überanpassung – wenn es zu sehr auf die Details der Trainingsdaten reagiert. Diese Balance ermöglicht eine gute Generalisierung, also die Fähigkeit, auf neuen Daten zuverlässig korrekte Vorhersagen zu treffen.

Die Herausforderung bei der praktischen Modelentwicklung ist jedoch, dass die perfekte Entscheidungsfunktion, oft als sogenannte Oracle-Funktion bezeichnet, in der Regel unbekannt ist. Diese hypothetische Funktion kennte alle zugrunde liegenden Zusammenhänge und Datenverteilungen. Da wir aber nur auf eine begrenzte Menge an Trainingsdaten zugreifen können, versuchen wir, uns diesem Ideal so gut wie möglich anzunähern. Die Auswahl der richtigen Modellklasse wird dabei zur zentralen Weichenstellung. Verschiedene Modelle lassen sich als unterschiedliche Funktionsräume verstehen, in denen man nach der bestmöglichen Lösung sucht.

Lineare Modelle bilden beispielsweise eine überschaubare Teilmenge aller möglichen Funktionen mit niedrigem Bias, aber möglicherweise hohem Fehler aufgrund mangelnder Flexibilität. Komplexere Modelle erweitern diesen Suchraum, bergen jedoch das Risiko höherer Varianz. Der Anspruch besteht darin, eine Modellklasse zu wählen, deren optimaler Vertreter den geringstmöglichen Abstand zur Oracle-Funktion hat und gleichzeitig durch die verfügbaren Daten gut gelernt werden kann. Zur Minimierung der Varianz greifen viele Praktiker auf Regularisierungstechniken zurück. Diese Methoden fügen dem Lernprozess eine Art Schutzmechanismus hinzu, um die Modellkomplexität zu begrenzen oder die Werte der Modellparameter zu kontrollieren.

Beispiele sind L1- und L2-Regularisierung, die dafür sorgen, dass das Modell nicht zu sprunghaft auf einzelne Trainingspunkte reagiert. Dadurch wird der Raum der möglichen Modelle effektiv eingeschränkt, was wiederum hilft, ein ausgewogenes Modell zu finden. Ein weiterer zentraler Aspekt ist die Wahl der richtigen Bewertungskriterien und Validierungsmethoden. Da der wahre Risiko- oder Fehlerwert nicht bekannt ist, wird das sogenannte empirische Risiko berechnet, basierend auf den beobachteten Trainingsdaten. Gute Praktiken wie Cross-Validation helfen, dieses empirische Risiko auf unterschiedlichen Datenpartitionen zu schätzen und so zu vermeiden, dass man ein Modell wählt, das nur auf einer spezifischen Stichprobe gut funktioniert.

In der Praxis ist das Bias-Varianz-Dilemma allgegenwärtig und betrifft nahezu alle Modelle und Anwendungen. Ob bei der medizinischen Diagnostik, beim autonomen Fahren oder bei Empfehlungen auf Streaming-Plattformen – die richtige Balance zwischen Modellvereinfachung und Flexibilität zu finden, entscheidet über den Erfolg oder Misserfolg eines Systems. Fortschritte im Bereich des maschinellen Lernens erlauben heute immer komplexere Modelle, aber der Bias-Varianz-Trade-off bleibt bestehen und stellt eine Art Navigationshilfe dar. Automatisierte Methoden wie Hyperparameter-Optimierung oder neuronale Architektur-Suche zielen darauf ab, die Modellkomplexität systematisch zu regulieren und das bestmögliche Gleichgewicht zu finden. Nichtsdestotrotz bleibt das grundsätzliche Verständnis des Trade-offs für Data Scientists und Entwickler essenziell.