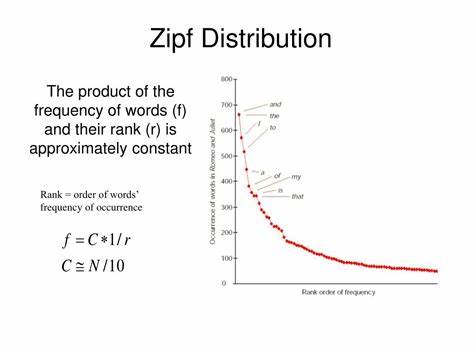
Zipfs Gesetz gehört zu den interessantesten Phänomenen, die unser Verständnis von Sprache, Gesellschaft und Natur bereichern. Es beschreibt eine scheinbar einfache, aber tiefgreifende Verteilung, die sich in vielen Bereichen findet – von der Häufigkeit von Wörtern in Texten bis hin zur Bevölkerung von Städten. Dieses Gesetz enthüllt ein Muster, das viele als Beweis für eine gewisse natürliche Ordnung im Chaos ansehen. Auch wenn es mathematisch betrachtet einfach ist, eröffnet Zipfs Gesetz vielseitige Perspektiven auf komplexe Systeme und ihre Dynamiken. Das grundsätzliche Prinzip von Zipfs Gesetz ist bestechend einfach: Wenn man Objekte nach ihrer Häufigkeit oder Größe sortiert, so besagt das Gesetz, dass die Häufigkeit des n-tplatzierten Objektes ungefähr dem Kehrwert seiner Position entspricht.
Konkret bedeutet das etwa, dass das zweithäufigste Wort halb so häufig auftritt wie das häufigste und das dritthäufigste rund ein Drittel so oft. Diese einfache Formel führt zu einer charakteristischen Kurve, die eine sogenannte Power-Law-Verteilung darstellt. Es entsteht eine klare Beziehung zwischen Rang und Häufigkeit, die überraschend konsistent in verschiedenen Kontexten beobachtet werden kann. Besonders in der Linguistik hat Zipfs Gesetz große Bekanntheit erlangt. Für viele Sprachen gilt, dass bestimmte Wörter enorm häufig vorkommen, während die Mehrheit nur sehr selten verwendet wird.
Ein klassisches Beispiel aus dem Englischen sind die Wörter "the", "of" und "and", die zu den Spitzenreitern zählen. Die Häufigkeit dieser Wörter folgt genau der Zipfschen Verteilung und lässt sich robust in fast allen natürlichen Sprachen nachweisen. Dieses Phänomen führt zu wichtigen Erkenntnissen: So können Forscher etwa unterscheiden, ob eine Sprache natürlich entstanden oder künstlich konstruiert wurde, denn konstruierte Sprachen weichen oft von diesem Muster ab. Auch in der Welt der Städte zeigt Zipfs Gesetz seine Gültigkeit. Betrachtet man die Bevölkerung von Großstädten, so ist häufig zu beobachten, dass die zweitgrößte Stadt etwa halb so viele Einwohner hat wie die größte, und die drittgrößte etwa ein Drittel so viele.
Dieses Verhältnis gilt nicht nur auf Länderebene, sondern lässt sich über verschiedene Kontinente und Epochen hinweg feststellen. Warum genau sich diese Verteilung einstellt, ist in der Wissenschaft weiterhin Gegenstand intensiver Debatten. Es spricht jedoch vieles für die Existenz selbstorganisierender Prozesse innerhalb von urbanen und sozialen Systemen. Überraschenderweise findet Zipfs Gesetz auch im Bereich der Cybersicherheit Anwendung. Wenn man beliebte Passwörter analysiert, folgt deren Häufigkeit ebenfalls einer Zipfschen Verteilung.
Ein kleiner Bereich an populären Passwörtern wird von vielen verwendet, während die meisten Passwörter nur von wenigen oder gar einer einzelnen Person genutzt werden. Diese Erkenntnis hat direkte Auswirkungen auf Sicherheitsstrategien, denn es zeigt die Notwendigkeit, häufig verwendete Passwörter zu vermeiden und robuste Alternativen zu fördern. Die Muster lassen sich hier als Warnsignal verstehen und verdeutlichen, wie weitreichend Zipfs Gesetz in ganz unterschiedlichen Feldern anwendbar ist. Interessanterweise trifft Zipfs Gesetz nicht auf die Häufigkeit einzelner Buchstaben zu. Anders als Wörter, die sich dynamisch in Sprachsystemen entwickeln, sind Buchstaben Bestandteile von festgelegten Schriftsystemen, die durch korrekte Regeln definiert werden.
Buchstabenhäufigkeiten spiegeln nicht das gleiche komplexe Selbstorganisationsverhalten wider und folgen daher anderen statistischen Verteilungen. Neben den direkten Anwendungen steht Zipfs Gesetz für ein tieferliegendes Muster komplexer, selbstorganisierender Systeme. Es scheint als hätte jede natürliche oder soziale Struktur eine Art Anziehungspunkt, der bewirkt, dass bestimmte Elemente bevorzugt auftreten und damit das System langfristig prägt. In der Forschung wird dies oft mit Begriffen wie Attraktor-Dynamik beschrieben, bei der das System sich in bestimmten Zuständen stabilisiert und dabei charakteristische Muster erzeugt. Manchmal wird allerdings angezweifelt, ob Zipfs Gesetz tatsächlich ein Naturgesetz ist oder eher ein Artefakt der Art, wie wir die Welt betrachten.
Untersuchungen mit zufällig generierten Wörtern haben gezeigt, dass diese ebenfalls Zipf-ähnliche Verteilungen aufweisen können. Dies lässt vermuten, dass Zipfs Gesetz auch durch die Wahl der Betrachtungsweise, nämlich die Benutzung des Wort-Rangs als unabhängige Variable, reproduzierbar ist. Somit könnte das Gesetz teilweise durch die Perspektive des Beobachters entstehen, was in philosophischer Hinsicht unsere Vorstellung von Objektivität in der Wissenschaft hinterfragt. Um das Phänomen besser zu verstehen, haben Forscher verschiedene Modelle entwickelt, die zum Beispiel eine Art präferentielle Anziehung simulieren. Die Idee dahinter ist, dass Wörter, die bereits häufig vorkamen, eine größere Wahrscheinlichkeit besitzen, erneut gewählt zu werden.
Diese so genannten Attraktor-Modelle können Zipfs Verteilung noch exakter abbilden und liefern Hinweise darauf, dass natürliche Prozesse oft von Rückkopplungen und Wahrscheinlichkeitsverstärkungen geprägt sind. Solche Modelle simulieren beispielsweise auch, wie Sprache entsteht oder wie Nutzerverhalten in Netzwerken verläuft. Ein spannender Aspekt ist dabei die Untersuchung, wie sich diese Verteilungen im Vergleich zu rein zufällig erzeugten Daten verhalten. Während zufällige Wortfolgen schon Zipf-ähnliche Muster zeigen können, ist in natürlichen Sprachen die Verteilung durchdachter und zeigt einen glatteren Verlauf. Dies unterstreicht, dass natürliche Sprachen auf einer effizienten Nutzung begrenzter Ressourcen basieren und auf Bedeutungsschwerpunkte hin optimiert sind, was in zufälligen Daten fehlt.
Die Diskussion, ob Zipfs Gesetz ein fundamentaler Mechanismus oder eher eine statistische Eigenschaft durch bestimmte Betrachtungsweisen ist, bleibt offen. Klar ist jedoch, dass es eine mächtige Linse bietet, um die Struktur von scheinbar chaotischen Systemen zu erforschen. Ob bei der Analyse von Wortverteilungen, Stadtgrößen, Internetnutzung oder Passwortverteilungen – Zipfs Gesetz führt immer wieder zu spannenden Erkenntnissen über das menschliche Verhalten und die zugrundeliegenden Dynamiken von Systemen. Darüber hinaus stellt sich die Frage, ob Zipfs Gesetz auch auf höheren Ebenen wie Satzstrukturen oder semantischen Clustern anwendbar ist. Da die meisten Sätze in der Regel einzigartig sind, ist eine Analyse durch reine Häufigkeiten schwierig.
Hier könnten jedoch Gruppierungen von semantisch ähnlichen Sätzen – etwa Begrüßungen oder Witze – ein nützliches Werkzeug sein, um Zipf-artige Verteilungen sichtbar zu machen. Diese Richtung eröffnet neue Forschungswege zur Analyse und Klassifizierung von Texten und Kommunikation. Zipfs Gesetz hat durch seine überraschende Universalität auch Einfluss auf andere Wissenschaftsbereiche, etwa in der Memetik, Informationswissenschaft oder sogar in der Erforschung künstlicher Intelligenz. Es hilft zu verstehen, wie sich Bedeutung, Relevanz und Nutzung innerhalb komplexer Systeme verteilen und wie sich daraus stabile Muster ableiten lassen. Die Idee, dass aus einfachen Regeln komplexe Strukturen entstehen, wird dadurch sehr anschaulich.
Seine Bedeutung zeigt sich auch daran, dass Zipfs Gesetz immer wieder Gegenstand von Diskussionen und Medienberichten ist. Es regt nicht nur Fachwissenschaftler zum Nachdenken an, sondern fasziniert auch die breite Öffentlichkeit, die in ihm ein Symbol für die versteckte Ordnung unserer Welt sieht. Youtube-Kanäle, Foren und Blogs widmen ihm Erklärvideos, Diskussionen und Experimente, was Zipfs Gesetz zu einem der bekanntesten Beispiele für Machtgesetze in der Popularwissenschaft macht. Egal ob in der Sprachwissenschaft, den Sozialwissenschaften, der Stadtplanung oder der Cybersecurity – Zipfs Gesetz bleibt ein Schlüsselwerkzeug, um den Puls komplexer Systeme zu messen und Muster zu erkennen, die anderenfalls verborgen blieben. Seine schlichte mathematische Form täuscht darüber hinweg, wie tiefgreifend und weitreichend seine Implikationen sind.
Zusammengefasst fasziniert Zipfs Gesetz nicht nur durch seine einfache Aussage, sondern durch die erstaunliche Universalität und die Vielzahl von Anwendungen. Es hilft, Verteilungen zu verstehen, die auf den ersten Blick zufällig erscheinen, und verweist auf das Zusammenspiel von Zufall, Ordnung und Entwicklung in natürlichen und sozialen Systemen. Darüber hinaus fordert es uns heraus, die Rolle des Beobachters und die Grenzen unserer Erkenntnis immer wieder kritisch zu hinterfragen und offen für neue Modelle und Erklärungen zu bleiben.