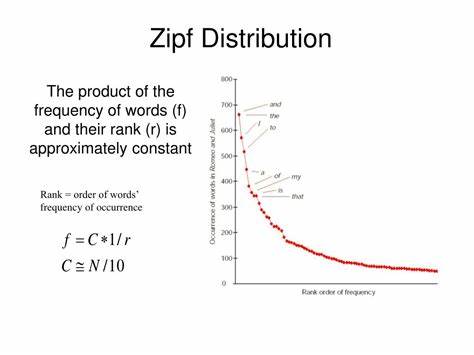
Zipfs Gesetz gehört zu den erstaunlichsten empirischen Gesetzen der Statistik und Linguistik. Es beschreibt eine Besonderheit, die in vielen Bereichen des Lebens und der Wissenschaft beobachtet wird: Wenn man Daten in absteigender Reihenfolge sortiert, ist der Wert des n-ten Elements oft ungefähr umgekehrt proportional zu seinem Rang. Das klingt zunächst recht abstrakt, doch in der Praxis zeigt Zipfs Gesetz verblüffende Muster, die von der Häufigkeit von Wörtern in einem Text bis hin zu den Größen von Städten reichen. Das wohl bekannteste Beispiel von Zipfs Gesetz findet sich in der Sprachwissenschaft. Wenn man alle Wörter eines Textes zählt und nach ihrer Häufigkeit sortiert, zeigt sich, dass das am häufigsten vorkommende Wort etwa doppelt so oft erscheint wie das zweithäufigste, dreimal so oft wie das dritthäufigste und so weiter.
Im Englischen etwa ist das Wort "the" das am häufigsten benutzte Wort, gefolgt von "of" und "and". Diese Verteilung folgt einem inversen Potenzgesetz, das mathematisch durch Zipfs Formel beschrieben wird. Interessanterweise blieb das Phänomen zunächst unerkannt, bis der amerikanische Linguist George Kingsley Zipf es in den 1930er Jahren systematisch untersuchte. Doch schon Jahrzehnte vor Zipf hatten andere Forscher ähnliche Beobachtungen gemacht, etwa Felix Auerbach, der Anfang des 20. Jahrhunderts die Größe von Städten in Relation zu ihrem Rang betrachtete.
Städte mit höherem Rang sind im Schnitt ungefähr proportional kleiner als die nächstgrößere Stadt. Diese Rang-Größen-Verteilung zeigt eine erstaunliche Regelmäßigkeit, die sich auch auf viele wirtschaftliche, soziale oder natürliche Systeme übertragen lässt. Die Bedeutung von Zipfs Gesetz reicht weit über die Linguistik hinaus. Ein bekanntes Beispiel ist die Stadtentwicklung: Wenn Städte nach ihrer Bevölkerungszahl geordnet werden, folgt die Verteilung genau dieser Regel. Große Metropolen wie New York oder Tokio sind im Verhältnis viel größer als kleinere Städte, und der Größenunterschied entspricht ziemlich genau der Inversen ihres Rangs.
Doch neuere Studien zeigen auch, dass dieses Gesetz nicht immer perfekt zutrifft – es gibt Abweichungen, die durch komplexere Mechanismen in der Gesellschaft bedingt sind. Was macht Zipfs Gesetz aber so faszinierend? Es offenbart, dass hinter scheinbar zufälligen oder chaotischen Verteilungen verborgene, universelle Prinzipien wirken. Das lässt sich auch auf die Entstehung von Wörtern in Sprachen übertragen, wo der "Aufwand" von Sprechern und Hörern eine Rolle spielt. Zipf selbst stellte den sogenannten "Prinzip der geringsten Anstrengung" auf, der besagt, dass Menschen dazu neigen, sich so auszudrücken, dass weder sie selbst noch ihr Gesprächspartner unnötigen Aufwand hat. Dieses Gleichgewicht führt zu der typischen Verteilung von Wortfrequenzen.
Mathematisch lässt sich Zipfs Gesetz durch eine spezielle Wahrscheinlichkeitsverteilung, die Zipf-Verteilung, oder eine Verallgemeinerung der harmonischen Reihe beschreiben. Dabei gibt es Parameter, die je nach Kontext die Form der Verteilung beeinflussen. Zum Beispiel berücksichtigt die Zipf-Mandelbrot-Verteilung einen zusätzlichen Korrekturfaktor, der manche Abweichungen von der idealen Gesetzmäßigkeit erklärt. Neben Sprache und Stadtgrößen findet Zipfs Gesetz Anwendung in Bereichen wie Wirtschaft, Biologie und sogar in der Musikwissenschaft. So zeigen Daten über Firmenumsätze, Einkommen oder die Häufigkeit von Musiknoten ähnliche Verteilungen.
Selbst in der Analyse von Genexpressionen in Zellen und bei der Untersuchung von Walgesängen konnten Parallelitäten entdeckt werden, die auf eine universelle Ausbreitung dieses Gesetzes hinweisen. Das Phänomen wirft eine Reihe von praktischen Fragen auf. Zum Beispiel kann Zipfs Gesetz bei der Textanalyse helfen, Autorenprofile zu erstellen oder die Spracheigenschaften unbekannter Texte zu entschlüsseln. In der Informationswissenschaft wird es genutzt, um die Effizienz von Suchmaschinen zu verbessern oder Muster in großen Textdatenbanken auszuwerten. Auch in der Kryptographie und bei der Suche nach außerirdischer Intelligenz spielt Zipfs Verteilung eine Rolle, denn Texte oder Signale, die natürlichen Sprachen entsprechen, weisen typischerweise Zipf-ähnliche Häufigkeiten auf.
Ein anderer spannender Aspekt sind die verschiedenen Erklärungsansätze für Zipfs Gesetz. Einige Forscher sehen es als Ergebnis von rein statistischen Prinzipien, die auch in zufällig erzeugten Texten entstehen können. Andere argumentieren, dass dynamische Prozesse wie das sogenannte "preferentielle Wachstum" – das Prinzip, dass Erfolg tendenziell weiteren Erfolg begünstigt – der Grund sein könnten. Dieses wird oft mit dem Bild "Die Reichen werden reicher" beschrieben und findet sich ebenfalls in urbanen Wachstumsprozessen und finanziellen Verteilungen wieder. Die Vielseitigkeit von Zipfs Gesetz macht es zu einem spannenden Forschungsfeld, das sich ständig weiterentwickelt.
Moderne Methoden, insbesondere im Bereich der Big Data und des maschinellen Lernens, eröffnen immer neue Möglichkeiten, dieses Phänomen zu untersuchen und zu verstehen. So könnte es etwa helfen, natürliche von künstlichen Sprachen oder sogar von Täuschungen zu unterscheiden. Trotz all dieser Fortschritte bleibt Zipfs Gesetz ein Rätsel, das Wissenschaftler fasziniert. Es zeigt, dass in vielen verschiedenen Systemen ein ähnliches Muster auftaucht, das Hinweise auf zugrunde liegende Ordnungsprinzipien gibt. Ob im geschriebenen Wort, in den Metropolen der Welt oder in den Lautäußerungen von Walen, Zipfs Gesetz verbindet unterschiedliche Welten durch eine einfache mathematische Beziehung.
In der heutigen Zeit, da Daten in riesigen Mengen generiert und analysiert werden, hat Zipfs Gesetz fast noch mehr Bedeutung gewonnen. Es unterstützt dabei, große Informationsfluten zu strukturieren, Zusammenhänge zu erkennen und Vorhersagen zu treffen. Insbesondere die Optimierung von Suchalgorithmen, das Verstehen von Sprachmodellen und die Analyse sozialer Netzwerke profitieren von diesem fundamentalen Gesetz. Zusammenfassend lässt sich sagen, dass Zipfs Gesetz ein universelles Muster offenbart, das tief in der Struktur von Sprache, Gesellschaft und Natur verwurzelt ist. Die Suche nach seinen Ursprüngen und Anwendungen ist nicht nur ein intellektuelles Abenteuer, sondern auch von praktischem Nutzen für Technologie, Wissenschaft und Wirtschaft.
Wer die Geheimnisse von Zipfs Gesetz entschlüsselt, gewinnt Einblicke in die Ordnung hinter dem Chaos unserer Welt.