Die Cardioid – ein Name, der sowohl in der Mathematik als auch in der angewandten Wissenschaft für staunende Blicke sorgt. Als eine der schönsten und faszinierendsten Kurven überhaupt, zeichnet sich die Cardioid durch ihre charakteristische Herzform aus. Sie ist weit mehr als ein ästhetisches Phänomen; sie hat tiefgründige mathematische Wurzeln und erscheint immer wieder an unerwarteten Orten in der Natur und Technik. Ihre einzigartige Form ist kein Zufall, sondern das Ergebnis von komplexen geometrischen und analytischen Prozessen, die sowohl Profis als auch Laien gleichermaßen begeistern. In diesem Beitrag wird die Cardioid in ihrer ganzen Vielseitigkeit beleuchtet – von ihrer Entdeckung über ihre mathematische Beschreibung bis hin zu praktischen Anwendungen und verblüffenden visuellen Beispielen.
Die Geschichte der Cardioid reicht weit zurück, doch genau lässt sich die erste Entdeckung nicht klar zuordnen. Bekannt ist, dass Étienne Pascal, Vater des berühmten Mathematikers Blaise Pascal, im 17. Jahrhundert die nahe verwandte Limakrose erforschte. Die eigentliche Cardioid erhielt ihren Namen allerdings erst im 18. Jahrhundert durch Johann Castillon, und weitere wichtige mathematische Erkenntnisse zur Kurve wurden von Philippe de la Hire veröffentlicht.
Die Cardioid ist damit ein historisches Objekt der Mathematik, das bereits seit mehreren Jahrhunderten die Aufmerksamkeit auf sich lenkt. Aber was genau ist eine Cardioid? Im Kern handelt es sich um eine Kurve, die beim Abrollen eines Kreises um einen gleich großen festen Kreis entsteht. Wird ein Punkt am rollenden Kreis markiert und seine Bahn verfolgt, entsteht die herzförmige Cardioid. Diese Konstruktion macht das Wesen der Cardioid anschaulich und ermöglicht es sogar, die Bewegung physisch zu demonstrieren. Dabei zeigt sich, wie scheinbar einfache geometrische Aktionen zu komplexen und ästhetisch ansprechenden Formen führen können.
Mathematisch lässt sich die Cardioid auf verschiedene Arten beschreiben. Besonders elegant ist dabei die Darstellung in Polarkoordinaten, wo sie durch die Gleichung r = a(1 - cos θ) definiert wird. Diese einfache Formel beschreibt eine geschlossene Kurve mit einer charakteristischen Spitze und einer glatten Herzform. Die Parametrisierung erlaubt es zudem, die Kurve mittels algebraischer und trigonometrischer Methoden zu analysieren und zu manipulieren. Dieses mathematische Fundament ist die Basis dafür, dass die Cardioid weit über die theoretische Ebene hinaus Bedeutung hat.
Ein besonders spannender Aspekt ist die Verbindung zwischen der Cardioid und der Mandelbrot-Menge, einem berühmten Objekt aus der komplexen Dynamik. Die Mandelbrot-Menge ist bekannt für ihre komplexen Strukturen und fraktalen Eigenschaften und zeigt im Zentrum eine herzförmige Region, die exakt einer Cardioid entspricht. Diese Entdeckung macht deutlich, dass die Cardioid nicht nur ein geometrisches Kurvenwunder ist, sondern auch in der Theorie der komplexen Zahlen eine herausragende Rolle spielt. So verbindet sie elementare Geometrie mit modernen Forschungsthemen. Neben der theoretischen Bedeutung hat die Cardioid auch praktische Anwendungen gefunden.
In der Audio- und Tontechnik ist das cardioide Mikrofon ein bewährtes Beispiel. Hier beschreibt die Cardioid die Empfindlichkeit des Mikrofons als Funktion der Schallquelle im Raum – maximale Empfindlichkeit von vorne und stark reduzierte von den Seiten und hinten. Diese Verhalten wird durch die sogenannte Richtcharakteristik des Mikrofon-Modells erklärt, das also auf einer Cardioid basiert. Das macht die Kurve nicht nur zu einer mathematischen Schönheit, sondern zu einem Werkstoff moderner Technik. Auch in der Optik und Physik taucht die Cardioid bemerkenswert auf.
Wer schon einmal einen Lichtstrahl in eine Kaffeetasse leuchten ließ, hat durchaus schon eine Cardioid gesehen, ohne es zu wissen. Die reflektierten Lichtstrahlen bilden an der Oberfläche der Flüssigkeit eine sogenannte Caustic-Kurve, die einer Cardioid entspricht. Diese physikalischen Muster entstehen durch die Reflexion von Licht an gekrümmten Oberflächen und sind ein hervorragendes Beispiel für die Verbindung von Mathematik und Naturphänomenen. Die genaue Erklärung erfolgt über die Theorie der Absolutreflexionen und die Berechnung der sogenannten Hüllkurven oder Envelopes von Linien. Besonders faszinierend ist, dass die Cardioid als Hüllkurve einer Familie von Geraden konstruiert werden kann.
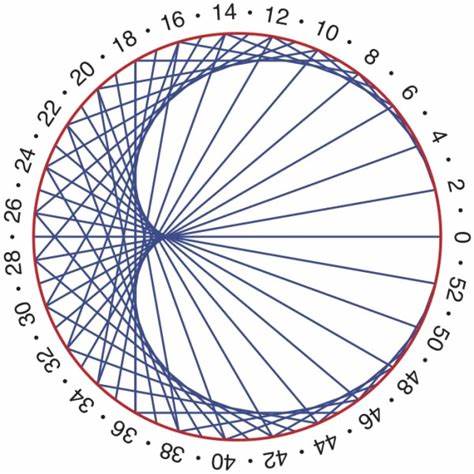
Indem man eine bestimmte Punktfolge an einem Kreis nummeriert und then Linien zwischen den Punkten mit doppelter Nummer modulo der Anzahl verbindet, entsteht eine beeindruckende visuelle Darstellung der Cardioid. Dieses einfache Spiel mit geraden Linien und modularer Arithmetik führt zu einer komplexen Kurve. Die Envelope-Technik ist in der Mathematik eine unverzichtbare Methode, um Kurven als Grenzen von Kurvenscharen zu definieren. Hier unterstützt sie das Verständnis der Cardioid und macht ihre Konstruktion sogar für Schüler und Interessierte zugänglich. Die vielfältigen Erscheinungsformen und die Kombination aus historischen, mathematischen und praktischen Aspekten machen die Cardioid zu einem Symbol für die Schönheit der Mathematik.
Sie zeigt, wie schon einfache Konzepte zu komplexen Mustern führen und wie diese Muster sowohl die Natur beschreiben als auch technische Lösungen ermöglichen. Somit überbrückt die Cardioid die Disziplinen und richtet sich an ein breites Publikum, vom Mathematiklehrer über den Ingenieur bis zum Naturbeobachter. Wer sich selbst mit der Cardioid beschäftigen möchte, kann dies mit einfachen Mitteln tun. Printable Vorlagen mit nummerierten Punkten auf einem Kreis ermöglichen es, die Verbindungslinien selbst zu zeichnen und so die Herzkurve entstehen zu lassen. Noch reizvoller sind Animationen und Flipbooks, die Schritt für Schritt die Entstehung der Cardioid visualisieren und so das Verständnis sowie die Faszination vertiefen.
Diese interaktiven Methoden fördern das intuitive Erfassen komplexer mathematischer Objekte. Im Zuge der modernen Digitalästhetik hat die Cardioid auch eine Rolle als Gestaltungselement gefunden. Ihre elegante Form eignet sich hervorragend für Logos, Grafiken und Designs, welche die Verbindung von Natur, Mathematik und Technik symbolisieren wollen. Damit ist die Cardioid nicht nur ein mathematisches Gebilde, sondern auch ein kultureller Referenzpunkt. Abschließend lässt sich sagen, dass die Cardioid mehr als eine simple Kurve ist.
Sie ist ein faszinierender Schatz der Geometrie, eine Brücke zwischen Theorie und Praxis und ein Beispiel dafür, wie Mathematik in vielfältigen Kontexten lebendig wird. Ob in der akustischen Welt der Mikrofone, bei Lichtreflexionen im Alltag oder im Denken über komplexe Zahlen und Fraktale – die Cardioid ist ein ständiger Begleiter, der zum Verweilen, Staunen und weiterforschen einlädt. Ihre geheimnisvolle Form verdeutlicht eindrucksvoll, dass Mathematik mehr ist als Zahlen und Formen; sie ist die Sprache, in der die Natur ihre schönsten Geschichten erzählt.