Jede Wissenschaftsdisziplin hat ihre eigene Art, Wissen zu strukturieren und zu verstehen. Während Mathematik oft durch detaillierte, abstrakte Definitionen und logischen Aufbau geprägt ist, so verlaufen die Erkenntniswege in den angewandten Wissenschaften häufig pragmatischer und funktionaler. Die Welt der Analogelektronik zeigt dabei auf faszinierende Weise, wie sich selbstbezügliche Abstraktionen als epistemologische Grundlage manifestieren. Dieser ungewöhnliche Ansatz bietet einen einzigartigen Weg, komplexe physikalische Realitäten zu modellieren, zu simulieren und zu verstehen – jedoch mit einer gewissen Portion Surrealismus und Witz. Mathematiker definieren Zahlen nicht einfach als „die Dinge, mit denen wir zählen“, sondern bauen sie schrittweise durch logische Konstruktionen auf.
Die Null entsteht aus der Kardinalität der leeren Menge, „Eins“ durch die Menge der leeren Menge und „Zwei“ durch eine Menge, die sowohl die leere Menge als auch deren Menge enthält. Ähnlich komplex lassen sich Reelle Zahlen und verschiedene Arten von Unendlichkeiten konstruieren. Dieses Vorgehen reflektiert eine epistemologische Haltung, die in der Welt der Zahlen durch präzise Definitionen und formale Logik das Verständnis schafft. Ganz anders gestaltet sich der Zugang in vielen Anwendungsbereichen, etwa in den Ingenieurwissenschaften oder der Softwareentwicklung. Hier stehen abstrakte funktionale Einheiten im Mittelpunkt – sogenannte Black Boxes oder APIs.
Die Details sind häufig weniger wichtig oder sogar irrelevant für den jeweiligen Anwendungsfall. Ein Webentwickler muss nicht die physikalischen Gesetzmäßigkeiten hinter Transistoren kennen – er setzt stattdessen auf vorgefertigte Bausteine, um produktiv zu sein. Dieses Konzept des „Abstrahierens“ ermöglicht es, komplexe Systeme effizient zu nutzen, ohne sich mit der tiefen Physik zu befassen. Die Welt der Analogelektronik bildet jedoch eine bemerkenswerte Ausnahme oder vielmehr eine faszinierende Mischung. Obwohl die zu modellierenden Phänomene direkt auf physikalischen Prinzipien basieren, werden sie häufig durch ideale, mathematisch elegante Abstraktionen beschrieben, die zunächst keinerlei Verbindung zur physischen Realität erfordern.
Nehmen wir als Beispiel den Widerstand. Ein idealer Widerstand ist in der Elektrotechnik eine einfache Gleichung I = V/R. Diese Formel beschreibt einen linearen Zusammenhang zwischen Strom (I) und Spannung (V) bei einem Widerstand (R). Rein physikalisch betrachtet ist ein Widerstand jedoch ein komplexes Objekt mit mikroskopischen Eigenschaften, Temperaturabhängigkeit und Fertigungstoleranzen. Trotzdem arbeitet der Ingenieur oftmals ausschließlich mit der idealen Form der Gleichung, um das Verhalten im Gesamtsystem zu verstehen und vorherzusagen.
Die physikalische Realität wird in gewisser Weise ausgeblendet – der Widerstand als Konzept und mathematische Abstraktion ist für die Praxis ausreichend. Ein weiterer Baustein ist der Kondensator. Idealerweise folgt er ebenfalls einer einfachen Beziehung: Die Spannung V über einem Kondensator entspricht dem Ladungsstrom, multipliziert mit der Zeit und geteilt durch die Kapazität C. Physikalisch gibt es jedoch zahlreiche Einschränkungen. Die tatsächliche Ladung und Entladung können nicht beliebig schnell erfolgen, besonders bei Elektrolytkondensatoren ist die Ionenbewegung begrenzt.
Anstatt die komplexen physikalischen Vorgänge direkt zu modellieren, zerlegt man reale Kondensatoren in Kombinationen idealer Bauelemente. Ein realer Kondensator wird beispielsweise durch einen idealen Kondensator in Serie mit einem Widerstand (RESR) dargestellt. Diese selbstbezügliche Vorstellung erweitert das Modell, macht es jedoch gleichzeitig abstrakter – der reale Kondensator wird quasi durch andere idealisierte Komponenten repliziert. Das Modell lässt sich weiter verfeinern. Elektromagnetische Effekte wie parasitäre Induktivitäten werden durch einen zusätzlichen idealen Induktor repräsentiert.
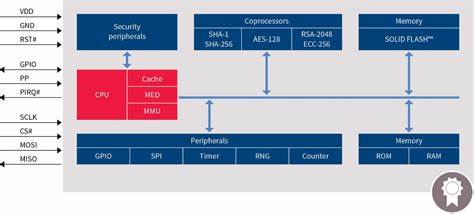
Selbst das langsame Selbstentladen des Kondensators wird durch einen parallel geschalteten Widerstand eingebaut. Man könnte theoretisch ewig weitermachen, um weitere Effekte wie temperaturabhängige Verluste hinzuzufügen. An dieser Stelle zeigt sich eine gewisse Paradoxie: Jedes reale physikalische Bauelement wird am Ende durch ein Netzwerk idealisierter, selbstbezüglicher Abstraktionen beschrieben, die alle zusammen den „realen“ Effekt simulieren. Dieses Vorgehen gilt natürlich nicht nur für einfache Bauelemente. Ein Transistor – das Herzstück moderner Elektronik – kann in seiner Funktionsweise so komplex sein, dass das entsprechende Modell im Datenblatt aus mehreren virtuellen Bauelementen besteht.
Dargestellt werden darin mehrere virtuelle Transistoren, Dioden, Spannungs- und Stromquellen, die das reale Bauelement auf abstrakter Ebene abbilden. Die Komplexität ist so enorm, dass diese Modelle nur mit softwaregestützter Simulation handhabbar sind. Die Programme, die hierfür verwendet werden, arbeiten mit proprietären, altmodischen Codierungen, die kaum mehr als verkettete Abstraktionen zulassen. Diese Methode – das ständige Erzeugen von neuen abstrakten Bausteinen zur Beschreibung der physikalischen Realität durch idealisierte Formeln und Modelle – ist ein charakteristisches Merkmal der Analogelektronik. Die Fachwelt akzeptiert sie als unumgänglich, auch wenn sie für Außenstehende bisweilen surreal wirkt.
Man kann es auch als eine Art Philosophie sehen: Anstatt zu versuchen, die mathematischen und physikalischen Grundlagen in ihrer Ursprünglichkeit vollständig zu durchdringen, akzeptiert man praktikable Ebenen idealisierter Modelle, die trotzdem miteinander interagieren und dadurch reale Phänomene erklären. Diese selbstbezügliche Herangehensweise hat weitreichende Konsequenzen für das Verständnis und die Entwicklung analoger Systeme. Zum einen ermöglicht sie es Entwicklern, komplexe Schaltungen zu entwerfen, obwohl niemand alle feinen physikalischen Details vollständig versteht. Andererseits führt sie aber auch zu einer gewissen Distanziertheit vom physikalischen Ursprung der Phänomene. Wichtig wird das Modell und seine Konsistenz in der Anwendung, nicht das letzte atomare Detail.
Darüber hinaus spiegelt sich in diesem Konzept auch die Herausforderung wider, die analoge Welt in der digitalen Technik zu verstehen und abzubilden. Denn letztlich muss ein Computer, dem wir eine Schaltung simulieren wollen, genau mit diesen idealisierten Modellen arbeiten. Sie sind die Sprache, mit der ein digitales System natürliche Prozesse approximiert – allerdings niemals perfekt, sondern nur mit einer gewissen Genauigkeit. Dieses Spannungsfeld zwischen Realität und Abstraktion ist eine treibende Kraft in der Weiterentwicklung von Hard- und Software für Elektronikdesign. In der breiteren Perspektive zeigt sich also: Die Erforschung und Nutzung analoger Systeme sind viel mehr als ein technisches Unterfangen, sie sind auch eine Auseinandersetzung mit Erkenntnisgrenzen und Modellen.
Die Art, wie Ingenieure und Wissenschaftler Wissen über reale Komponenten und deren Zusammenwirken konstituieren, ist ein Wechselspiel zwischen idealisierter Mathematik und physikalischer Wirklichkeit, vermittelt durch selbstbezügliche Abstraktionen. Dies macht gerade die Analogelektronik zu einem spannenden Feld, das viel über die Art und Weise verrät, wie Menschen mit Komplexität und Unsicherheit umgehen. Wer sich mit diesem Thema vertieft auseinandersetzt, wird nicht nur technisches Wissen gewinnen, sondern auch neue Einsichten in die Philosophie der Wissenschaft und Technik erlangen. Analoge Elektronik ist damit ein Beispiel für eine spezielle epistemologische Haltung, bei der das Modell nicht nur ein Abbild der Realität ist, sondern selbst eine eigene Realität innerhalb des Denkens und Handelns schafft. Diese Betrachtungsweise wertet das Verständnis analoger Systeme nicht ab, sondern hebt es vielmehr auf eine Metaebene.
Sie zeigt, dass unser Wissen über die Welt immer auch darauf beruht, wie wir sie abstrahieren, beschreiben und konstruieren. Selbstbezügliche Abstraktionen in der Analogelektronik sind deshalb mehr als nur Modellierungstechniken – sie sind Ausdruck einer eigentümlichen, aber genialen Teildisziplin menschlichen Erkenntnisstrebens.