Innovative Grundlagen der trapezförmigen Origami-Metamaterialien: Fundamentale Formen und ihre Charakterisierung

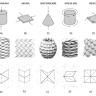
Origami, die jahrhundertealte Kunst des Papierfaltens, hat sich in den letzten Jahrzehnten von einer künstlerischen Praxis zu einem wissenschaftlichen und ingenieurtechnischen Forschungsfeld entwickelt. Insbesondere Origami-Metamaterialien – speziell entworfene faltbare Strukturen – gewinnen zunehmend an Bedeutung. Diese flexiblen, leichten und dennoch robusten Systeme nutzen die geometrischen Prinzipien des Origami, um außergewöhnliche mechanische Eigenschaften zu ermöglichen. Ein besonderer Forschungsfokus liegt dabei auf trapezförmigen Origami-Metamaterialien, deren grundlegende Formen und Deformationsmuster als Schlüssel zum Verständnis ihrer vielfältigen Einsatzmöglichkeiten dienen. Traditionell konzentrieren sich Studien im Bereich faltbarer Materialien häufig auf parallelogrammbasierte Origami-Tessellationen, wie die bekannte Miura-ori-Faltung.

Diese Muster sind für ihre hohe Biegsamkeit und bemerkenswerte Eigenschaften wie negative Poisson-Verhältnisse bekannt. Sie bestehen aus parallelen Linien und symmetrischen Flächen, was ihre theoretische Modellierung vereinfacht und zugleich bestimmte mechanische Reaktionen erzwingt. Allerdings begrenzen die starren geometrischen Rahmen parallelogrammbasierter Muster die Vielfalt der mechanischen Anpassungen, die möglich sind. Im Gegensatz dazu ermöglichen trapezförmige Flächenelemente durch ihre geringere Symmetrie eine größere Komplexität in der Struktur und damit eine erweiterte Bandbreite an Verformungsmodi. Das Verständnis fundamentaler Formen für trapezförmige Origami-Metamaterialien basiert auf der Untersuchung ihrer isometrischen, also nicht-dehnbaren, Linear- und Nichtlinear-Deformationen.

Isometrie bedeutet bei Origami, dass die einzelnen Flächen sich nicht dehnen oder komprimieren, sondern sich ausschließlich durch Falten und Biegen bewegen. Dabei tritt eine Differenzierung der Energieebenen zutage: Die Energie, die zum Biegen der einzelnen Falte notwendig ist, skaliert kubisch mit der Materialdicke, während Streckungen der Paneele linear mit der Dicke skaliert werden. Durch diese Differenzierung ist der elastische Verformungsprozess quasi-statisch und von den Materialien unabhängig, was bedeutet, dass das Kinematikverständnis des Faltmusters den ausschlaggebenden Faktor für das Materialverhalten darstellt. Im Kern der aktuellen Forschung steht die Erweiterung der bisher bekannten Modelle für parallelogrammbasierte Origami hin zu trapezförmigen Mustern. Solche Muster bilden quasi-zylindrische Flächen mit vierseitigen Elementen, deren benachbarte Zellen um eine gemeinsame Rotationsachse versetzt sind.

Diese Eigenart unterscheidet sie grundlegend von den meist flachen oder ebenen Plattformen parallelogrammbasierter Origami und bietet zugleich neue Freiheitsgrade in der Strukturmechanik. Die grundlegenden Formen der Struktur werden durch das sogenannte erste und zweite Fundamentale Form beschrieben. Das erste Fundamentale Formenkonzept definiert die Metrik der Oberfläche, indem es die inneren Abstände festlegt, wohingegen das zweite Fundamentale Form die Krümmung und damit die räumliche Einbettung der Oberfläche beschreibt. Die Kombination dieser grundlegenden geometrischen Größen ermöglicht es, die effektiven mechanischen Eigenschaften der Origami-Strukturen zu erfassen und in ein kontinuierliches Modell zu übersetzen, das von diskreten Faltmustern abstrahiert. Im Falle der trapezförmigen Origami-Metamaterialien finden sich zwei essenzielle isometrische Verformungsmodi.

Der erste ist ein rigider Atemmechanismus, bei dem die Struktur gleichmäßig „atmet“, sprich sie expandiert oder kontrahiert ohne dabei die einzelnen Flächen zu verformen, sondern ausschließlich durch Falten. Der zweite Modus ist eine nicht-rigide Scherung, welche eine komplexere, energiesparende Umgestaltung der Struktur bewirkt und dabei mit Veränderungen in der Orientierung der Hauptkrümmungsrichtungen einhergeht. Für die analytische Modellierung dieser Vorgehensweise wurden spezielle Ausschlussbedingungen für die Kompatibilität von Faltungen innerhalb einer Zelle entwickelt. Diese wurden in Form von Kompatibilitätsdiagrammen visualisiert, die sowohl die Amplituden der Faltbewegungen an den Knotenpunkten (Vertices) als auch die Biegungen der Fläche (Faces) abbilden. Durch diese duale Betrachtung ist es möglich, die Verformungen präzise zu charakterisieren und ein geschlossenes System von Gleichungen zu formulieren, das sowohl starre als auch flexible Faltungsmechanismen beschreibt.

Eine bedeutende Erweiterung des Forschungsgebiets stellt die Einführung der sogenannten Arc-Morph-Familie von Origami-Metastructures dar. Diese Kreationen vereinigen die Geometrien trapezförmiger Origami mit den variantenreichen Modifikationen der Arc-Miura- und Morph-Muster zu einer vielseitigen Designplattform mit drei Freiheitsgraden: zwei Winkelparameter α und β, die die Sektorwinkel der einzelnen Knoten bestimmen, sowie das Verhältnis der Kantenlängen q/p, welches die Proportionen der trapezförmigen Flächen zueinander definiert. Die Arc-Morph-Origami zeigen vielfältige Faltmechanismen sowie eine ausgeprägte räumliche Gestaltcharakteristik durch die räumliche Anordnung und Rotation der Einheitszellen. Experimente mit dem Arc-Miura-Modell, einer speziellen Untergruppe der Arc-Morph-Konstruktionen mit entwickelbarer Geometrie, belegen die theoretischen Vorhersagen. Gefertigt aus Polypropylen zeigt das Material sowohl die rigiden Atembewegungen als auch die komplexeren Scherbewegungen als Reaktion auf externe Belastungen.

Dabei gelingt es, die theoretisch vorhergesagten Beziehungen zwischen Höhe und Radius der quasi-zylindrischen Strukturen präzise im Experiment zu bestätigen. Die Verwendung monolithisch gefertigter, entwickelbarer Muster ermöglicht zudem qualitative Beobachtungen der nicht-rigiden Scherbewegungen, die besonders in Anwendungen mit heterogenen Lasten bedeutend werden. Die aerodynamische und mechanische Anpassungsfähigkeit trapezförmiger Origami eröffnet einen Horizont an Anwendungen. Besonders in der Entwicklung flexibler Tragwerksstrukturen, leichter Überzüge für Robotik und bei der Herstellung anpassungsfähiger Bauteile für Luft- und Raumfahrttechnik leisten diese metamaterialien einen entscheidenden Beitrag. Durch die gezielte Gestaltung der Faltmuster können maßgeschneiderte Effekte wie variable Steifigkeiten, kontrollierte Ausdehnungen und richtungsabhängige Krümmungen erzielt werden, die mit konventionellen Materialien nur schwer zu realisieren sind.

Die Verbindung zwischen diskreten geometrischen Konstruktionen und dem zugrundeliegenden kontinuierlichen Modell ist dabei von zentraler Bedeutung. Die Coarse-Graining-Methode, die durch das Aggregieren von Einzelzellbewegungen zu einem globalen Verformungsmodell führt, erlaubt eine präzise Beschreibung des mechanischen Verhaltens großer Origami-Flächen. Diese Methode berücksichtigt die komplexen Wechselwirkungen zwischen den Faltungen und schafft den Brückenschlag zu klassischen Theorien elastischer Platten und Schalen, wodurch eine integrierte Sicht auf Materialeigenschaften und Strukturmechanik entsteht. Zukünftige Forschungen könnten sich verstärkt der Entwicklung von noch komplexeren Faltmustern widmen, beispielsweise durch den Einbezug nicht-paralleler Kanten oder die Variation der Flächentypen innerhalb einer Tessellation. Darüber hinaus erfordert die experimentelle Validierung insbesondere der nicht-rigiden Verformungsmodi ausgeklügelte Messverfahren und belastungsspezifische Anordnungen, welche die gezielte Aktivierung einzelner Moden ermöglichen.

Die Kombination von Materialwissenschaft, Geometrie und Ingenieurwesen macht Origami-Metamaterialien zu einem dynamischen Gebiet mit großem Innovationspotenzial. Die Erkenntnisse zu den fundamentalen Formen von trapezförmigen Origami-Metamaterialien erweitern nicht nur das theoretische Verständnis, sondern eröffnen insbesondere für die praktische Ausgestaltung multifunktionaler, adaptiver Materialien neue Perspektiven. Ihre Anwendungen reichen von der Entwicklung effizienter Transport- und Verpackungslösungen bis hin zu adaptiven Schutzstrukturen in Architektur und Technik. Als lebendiges Beispiel für die Symbiose von Kunst und Wissenschaft inspiriert Origami die Materialforschung zu neuen Wegen der flexiblen, sicheren und ressourcenschonenden Gestaltung unserer gebauten Umwelt.