Laws, Potenzgesetze und Statistiken: Die Kunst der Datenanalyse In einer Welt, die zunehmend von Daten dominiert wird, ist die richtige Analyse und Interpretation dieser Daten von entscheidender Bedeutung. Insbesondere in den Naturwissenschaften gewinnt der Umgang mit Statistiken und die Ableitung von Gesetzmäßigkeiten immer mehr an Bedeutung. Der Physiker Mark Buchanan bringt in seinem Aufsatz „Laws, power laws and statistics“ wichtige Aspekte dieser Thematik auf den Punkt, und wir werfen einen Blick auf die Bedeutung von Gesetzen und Potenzgesetzen sowie auf die Herausforderungen der statistischen Datenanalyse. Zunächst ist es wichtig zu verstehen, was ein Gesetz in der Wissenschaft bedeutet. Ein Gesetz ist im Grunde genommen eine verallgemeinerte Regelmäßigkeit, die auf empirischen Beobachtungen basiert.
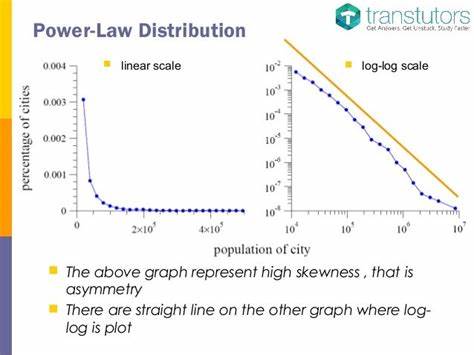
Dies kann eine mathematische Beziehung zwischen verschiedenen Variablen oder eine wiederkehrende Beobachtung in der Natur sein. Ein bekanntes Beispiel ist das Gutenberg-Richter-Gesetz, das die Verteilung der Erdbebenstärken beschreibt. Es stellt fest, dass die Wahrscheinlichkeit eines Erdbebens mit einer bestimmten Energie E invers zu E² abnimmt. Dieses Gesetz verdeutlicht das Fehlen einer inhärenten Skala für Erdbeben und hat weitreichende Konsequenzen für das Verständnis geophysikalischer Phänomene. Potenzgesetze sind eine besondere Form dieser Gesetze, die in vielen Naturphänomenen auftreten.
Sie zeichnen sich dadurch aus, dass die Beziehung zwischen zwei Größen einen konstanten Exponenten aufweist, was oft in der Form y = k * x^α dargestellt wird. Dies bedeutet, dass kleine Ereignisse häufig auftreten, während große Ereignisse vergleichsweise selten sind. Diese Verteilung ist in vielen Bereichen zu beobachten, von der Verteilung von Vermögen bis hin zur Häufigkeit von Tierarten in einem bestimmten Gebiet. Ein bedeutendes Problem bei der Analyse von Daten und der Aufstellung von Hypothesen ist die Qualität der zugrunde liegenden Daten. Hochwertige Daten sind selten, und die Interpretationen basieren oft auf unzureichenden Informationen.
Dies führt dazu, dass Forscher manchmal zu unwissenschaftlichen oder falschen Schlussfolgerungen gelangen. Oft werden methodische Fehler gemacht, etwa bei der Anwendung von Regressionsanalysen. Diese gängigen statistischen Verfahren setzen bestimmte Voraussetzungen voraus, die nicht immer gegeben sind. Buchanan zitiert eine wichtige Arbeit von Aaron Clauset und seinen Kollegen, die auf die Problematik der linearen Regression bei log-transformierten Daten aufmerksam machen. Wenn man Daten logarithmisch transformiert, ändern sich die ursprünglichen Verteilungseigenschaften und die Annahmen über die Fehlerverteilung, was zu verzerrten Ergebnissen führen kann.
Die Forscher schlagen vor, dass eine gründliche Analyse nicht nur auf der Anpassung einer Funktion an die Daten basiert, sondern auch eine Prüfung der zugrunde liegenden Hypothese erfordert. Ein kritischer Schritt bei der Untersuchung von Potenzgesetzen besteht darin, die Wahrscheinlichkeit zu ermitteln, dass die tatsächlichen Daten durch Zufall entstehen könnten, wenn man annimmt, dass es ein zugrunde liegendes Potenzgesetz gibt. Diese Analyse kann helfen festzustellen, ob die Annahme eines Potenzgesetzes überhaupt gerechtfertigt ist. Sollte diese Annahme scheitern, ist es unwahrscheinlich, dass die Daten tatsächlich ein Potenzgesetz widerspiegeln. Wenn die Annahme jedoch bestehen bleibt, reicht das nicht aus, um zu behaupten, dass die Daten tatsächlich einem Potenzgesetz folgen.
In einem nächsten Schritt sollte man die Güte der Anpassung zwischen dem Potenzgesetz und anderen möglichen Verteilungen, wie beispielsweise einer exponentiellen Verteilung, vergleichen. Diese methodischen Überlegungen mögen auf den ersten Blick pedantisch erscheinen, doch ihre Bedeutung zeigt sich in den Ergebnissen der analytischen Arbeiten von Clauset et al. Sie haben zahlreiche Datensätze, für die zuvor Potenzgesetze postuliert wurden, erneut analysiert. Dabei haben sie festgestellt, dass einige Daten, wie die Verteilung von Waldbränden oder die Verlinkungen von Webseiten, tatsächlich moderat gut von Potenzgesetzen beschrieben werden können. Andere Datensätze, wie beispielsweise die Verteilung von Wohlstand, zeigten dagegen keine deutliche Übereinstimmung mit einem Potenzgesetz.
Die Wiederentdeckung solcher Ergebnisse durch gründliche statistische Analysen bringt uns zu einem zentralen Punkt: Die menschliche Neigung, aus scheinbar einfachen Regressionstechniken falsche Schlussfolgerungen zu ziehen. Dies geschieht oft unbeabsichtigt, kann jedoch erhebliche Auswirkungen auf das gesamte Forschungsfeld haben. Die Verwendung unverifizierter statistischer Methoden führt dazu, dass Forscher und die breite Öffentlichkeit falsche Vorstellungen über die Natur der Daten entwickeln, was letztlich die wissenschaftliche Integrität gefährdet. Bereits ein kleiner Anstieg der statistischen Sophistizierung kann die Qualität der Forschung jedoch erheblich verbessern. Die Fähigkeit, kritisch mit Daten umzugehen, fördert nicht nur die Genauigkeit, sondern bewahrt auch das Vertrauen in die Wissenschaft als Mittel zur Entdeckung der Wahrheit und zur Trennung von Wunschdenken.
Ein weiteres bemerkenswertes Element in Buchanans Schreibweise ist die Betonung der kreativen Seite der Wissenschaft. Während Gesetze und Statistiken oft als trockene Materie erscheinen, sind sie eng mit dem kreativen Prozess der Theoriebildung und -überprüfung verbunden. Wissenschaftler müssen sich ständig neuen Daten und Theorien stellen und sich anpassen, wobei sie sich nicht auf das verlassen können, was offensichtlich oder „selbstverständlich“ erscheint. In einer zeitgenössischen Welt, in der Datenanalysen immer zugänglicher werden, aber auch gefährlicher, ist es unerlässlich, dass Forscher und die Öffentlichkeit sich der potenziellen Fallstricke bewusst sind. Der Umgang mit Daten erfordert kritisches Denken, Übung und eine solide Methodik.
Nur so kann sichergestellt werden, dass die gewonnenen Erkenntnisse den rigorosen Standards wissenschaftlicher Genauigkeit entsprechen. Zusammenfassend lässt sich sagen, dass die Untersuchung von Gesetzen und Potenzgesetzen in der Wissenschaft nicht nur eine technische Disziplin ist, sondern auch einen kreativen und oft herausfordernden Prozess darstellt. Forscher müssen lernen, die Fallstricke und Herausforderungen der Datenanalyse genau zu erkennen, um schlüssige und verlässliche Ergebnisse zu erzielen. Letztlich ist es die Mischung aus sorgfältiger Datenanalyse und kreativem Denken, die die Wissenschaft voranbringt und uns hilft, die komplexe Welt, in der wir leben, besser zu verstehen.