Das Good Regulator Theorem zählt zu den bedeutendsten, aber zugleich auch zu den am wenigsten intuitiv nachvollziehbaren Ergebnissen in der Theorie der Regelungssysteme. Bereits im Jahr 1970 formuliert von Conant und Ashby, behauptet das Theorem eine einfache, aber tiefgründige Wahrheit: Jeder gute Regler eines Systems muss im Grunde ein Modell dieses Systems sein. Doch was bedeutet das genau? Und warum wird gerade diese Erkenntnis als so grundlegend für die Agenten- und Steuerungstheorie betrachtet? Um diese Fragen zu beantworten, wollen wir die wesentlichen Aspekte des Good Regulator Theorems Schritt für Schritt erläutern und verständlich machen. Zunächst steht die Grundidee eines Regelsystems im Mittelpunkt. Stellen Sie sich ein Systemvariable vor, die zufälligen äußeren Einflüssen unterliegt.
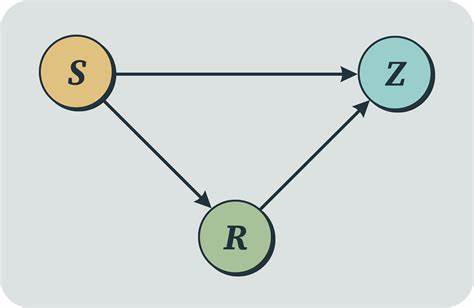
Ein Regler muss diese Störungen erfassen und durch geeignete Aktionen dafür sorgen, dass das Systemziel erreicht wird – ähnlich einem Thermostat, das mithilft, eine Raumtemperatur trotz wechselnder Außentemperaturen stabil zu halten. Im formalen Kontext wird die Systemvariable mit S bezeichnet, der Reglerzustand mit R und das Ergebnis der Regelung mit Z. Das Theorem analysiert, welche Eigenschaften R haben muss, um die bestmögliche Kontrolle über Z zu gewährleisten. Grundlage der Analyse ist eine grafische Darstellung in Form eines gerichteten azyklischen Bayes'schen Netzes. Dabei wirken Systemvariable S und Reglervariable R gemeinsam auf die Ergebnisvariable Z ein.
Das Besondere ist, dass R sich abhängig von S verhält, das heißt, die Verteilung von R ist konditioniert auf den Zustand S. Anders ausgedrückt: Der Regler passt sein Verhalten an den aktuellen Systemzustand an. Das Ziel besteht darin, die Unsicherheit beziehungsweise die Entropie der Ergebnisvariable Z zu minimieren, um eine möglichst präzise Kontrolle zu erlangen. Die Entropie ist ein Konzept aus der Informationstheorie und beschreibt die Unbestimmtheit einer Zufallsvariablen. Eine geringere Entropie bedeutet, dass das Ergebnis vorhersehbarer ist und damit im Sinne der Regelung besser kontrolliert wird.
Was macht also einen "guten" Regler aus? Im Sinne des Good Regulator Theorems wird ein guter Regler definiert als einer, der die Entropie von Z minimiert und dabei keine unnötige Komplexität aufweist. Das bedeutet konkret, wenn zwei Regler das gleiche Ergebnis erzielen, von denen einer deterministisch arbeitet und der andere zufällig, wird der deterministische Regler bevorzugt, da er einfacher und effektiver ist. Das mathematische Herzstück des Theorems ist die Behauptung, dass ein solcher guter Regler R immer als eine deterministische Funktion der Systemvariable S dargestellt werden kann. Einfach gesagt heißt das, dass für jeden Zustand von S genau ein bestimmter Wert von R gewählt wird, ohne Zufallselemente. In der Sprache der Wahrscheinlichkeitsverteilungen bedeutet dies, dass die bedingte Verteilung P(R|S) nur Werte 0 oder 1 annimmt und somit deterministisch ist.
Warum ist das so? Der Beweis des Theorems nutzt die sogenannte Konkavität der Shannon-Entropie. Die Entropiefunktion verhält sich so, dass jede Erhöhung der "Ungleichgewicht" innerhalb einer Wahrscheinlichkeitsverteilung zu einer niedrigeren Entropie führt. Wird beispielsweise die Wahrscheinlichkeit eines Ergebnisses erhöht, das ohnehin schon am wahrscheinlichsten ist, sinkt die Entropie insgesamt. Deshalb macht es aus entropischer Sicht keinen Sinn, Zufall in das Reglerverhalten einzubauen, wenn dadurch unterschiedliche Resultate erzielt werden – denn durch die Konzentration auf einen einzigen Zustand können die Unsicherheiten verringert werden. Eine wesentliche Zwischenaussage des Theorems, die sogenannte Hauptlemma, besagt, dass wenn ein Regler mehrere unterschiedliche Aktionen mit nicht-null Wahrscheinlichkeit bei einem bestimmten Systemzustand hervorruft und diese Aktionen unterschiedliche Ergebnisse im System bewirken, dann ist der Regler nicht optimal.
Er könnte durch einen Regler ersetzt werden, der diejenige Aktion mit der wahrscheinlichsten oder besten Auswirkung immer auswählt, was die Entropie des Ergebnisses reduziert. Das Theorem macht darüber hinaus deutlich, dass ein guter Regler die Systemvariable gewissermaßen "nachbildet". Da R eine eindeutige Funktion von S ist, spiegelt R alle relevanten Informationen über den Systemzustand wider. Aus diesem Grund stellen Conant und Ashby fest, dass ein guter Regler ein "Modell" des Systems sein muss – zumindest in einem sehr vereinfachten und formalen Sinn. Allerdings ist kritisch anzumerken, dass diese Aussage im engeren technischen Sinne verstanden werden muss.
Ein solcher "Modellbegriff" entspricht nicht unbedingt der umfassenden Vorstellung eines simulierten oder erklärenden Modells, wie es in der Praxis oft verwendet wird. Um die Abstraktheit der Aussagen zu verdeutlichen, sei ein Beispiel angeführt: Angenommen, das System hat drei Zustände und der Regler drei mögliche Reaktionen, die über eine Funktion ψ auf die Ergebnisvariable Z abgebildet werden. Wenn der Regler bei einem Systemzustand zufällig zwischen zwei Aktionen mit unterschiedlichen Ergebnissen wählt, steigt die Entropie der Resultate. Eine bessere Strategie ist es, immer diejenige Aktion zu wählen, die das Ergebnis mit der höchsten Wahrscheinlichkeit hervorruft, wodurch Entropie und Unsicherheit abnehmen und der Regler somit besser wird. Wenn jedoch zwei verschiedene Aktionen bei gleichem Systemzustand zum exakt gleichen Ergebnis führen, dann ist es unerheblich, mit welcher Wahrscheinlichkeit der Regler diese auswählt – da der Ausgang stets identisch ist, bleibt die Entropie unverändert.
Dennoch wird hier die unnötige Komplexität einer Zufallsentscheidung kritisiert, weshalb ein deterministischer Regler bevorzugt wird. Die Bedeutung des Good Regulator Theorems geht weit über einfache Beispiele wie Thermostate hinaus. In moderner Regelungstechnik, Agentenforschung und der Künstlichen Intelligenz verdeutlicht das Theorem die Notwendigkeit eines genauen Verständnisses des Umweltzustands, um effektive Steuerung oder Anpassung zu ermöglichen. Besonders im Bereich von intelligenten Agenten, die in dynamischen und unsicheren Umgebungen agieren, zeigt das Theorem, dass erfolgreiche Regelung eng mit der internen Repräsentation oder dem "Modell" der Umwelt verknüpft ist. Allerdings darf nicht übersehen werden, dass das Good Regulator Theorem einige Annahmen trifft, die in der Praxis nicht immer erfüllt sind.
Zum Beispiel setzt es voraus, dass der Regler perfekten Zugriff auf den Systemzustand hat, was in realen Anwendungen meist nicht der Fall ist. John Wentworth und andere Forscher haben das Theorem erweitert und verfeinert, um situationsabhängigere und robustere Formen zu untersuchen, in denen Regler eingeschränkte oder verrauschte Informationen berücksichtigen müssen. Kritisch hinterfragt wird außerdem die Bedeutung der Aussage, dass ein guter Regler ein "Modell" des Systems sein muss. Viele Fachleute zeigen auf, dass das Theorem in seiner formalen Auslegung schlicht sagt, dass der Regler deterministisch auf den Systemzustand reagieren sollte, was ein sehr schwaches und nicht wirklich reichhaltiges Verständnis von "Modell" ist. In komplexeren oder realweltlichen Szenarien ist es nötig, tiefergehende Modelle mit schätzungsbasierten, probabilistischen oder adaptiven Eigenschaften anzulegen.