In der Welt der Computergrafik und der numerischen Simulation spielen Signierte Abstandsfunktionen (SDF) eine entscheidende Rolle bei der Darstellung und Verarbeitung von Oberflächen. SDFs ermöglichen es, komplexe geometrische Formen präzise und effizient zu modellieren, was unter anderem in Anwendungen wie Physiksimulationen, Rendering oder 3D-Druck von großem Nutzen ist. Trotz der breiten Anwendung sind jedoch Herausforderungen bei der exakten Berechnung von SDFs gegeben, insbesondere wenn es darum geht, die exakte Lage der Oberfläche, das sogenannte Nullniveau, zu erhalten. Hier setzt eine innovative Technik an, die auf der Einbettung impliziter Oberflächen in neuronale Netzwerke basiert und so eine präzise SDF-Berechnung ermöglicht. Diese Methode wurde von Pierre-Alain Fayolle von der Universität Aizu entwickelt und in der renommierten „Journal of Computer Graphics Techniques“ vorgestellt.
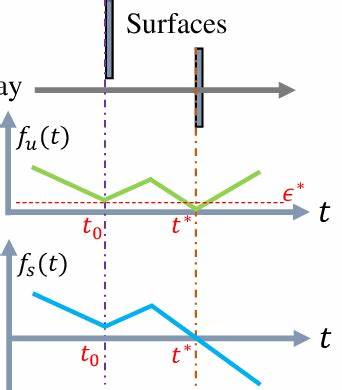
Die Grundlagen der Problemstellung beruhen darauf, dass eine implizite Oberfläche durch eine Funktion definiert ist, deren Nullstelle die Oberfläche selbst repräsentiert. Für viele Anwendungen ist es notwendig, daraus eine signierte Abstandsfunktion zu erzeugen, die nicht nur den Abstand eines Punktes zur Oberfläche angibt, sondern auch die Nähe zum exakten Nullniveau garantiert. Die Schwierigkeit liegt bei herkömmlichen Verfahren darin, dass bei der Approximation der SDF der genaue Nulllevel leicht verloren gehen kann, was zu ungenauen Darstellungen und Fehlern bei nachfolgenden Berechnungen führt. Die neu eingeführte Methode besitzt die Besonderheit, dass sie das ursprüngliche Nullniveau der impliziten Oberfläche exakt bewahrt. Das zentrale Element dieses Verfahrens ist die Konstruktion eines neuronalen Netzwerks, in dessen letzter Schicht die Ausgabe mit der impliziten Oberflächenfunktion oder einer geglätteten Version ihrer Signum-Funktion multipliziert wird.
Dadurch wird sichergestellt, dass die resultierende Funktion exakt bei Null liegt, wo auch die ursprüngliche Oberfläche definiert ist. Das Training des neuronalen Netzwerks erfolgt anhand einer Verlustfunktion, die spezielle Bedingungen charakterisiert, die eine signierte Abstandsfunktion erfüllen sollte. Eine solche Bedingung ist die Eikonalgleichung, eine fundamentale partielle Differentialgleichung, die für SDFs maßgeblich ist. Alternativ kann der Trainingsprozess auch auf eine approximative Formulierung mittels des p-Laplace-Operators zurückgreifen, die flexiblere Anpassungsmöglichkeiten bietet. Beide Ansätze zielen darauf ab, die Eigenschaften einer idealen SDF bestmöglich abzubilden und gleichzeitig die genaue Beibehaltung des Nullniveaus zu gewährleisten.
Die Anwendung neuronaler Netze in der Geometrieverarbeitung gewinnt immer mehr an Bedeutung, da sie eine flexible und leistungsstarke Methode zur Darstellung komplexer Funktionen bieten. In diesem Kontext zeigt die hier beschriebene Technik, wie die Kombination von tiefen Lernmodellen mit mathematischen Modellen aus der Differentialgleichungstheorie zu hochpräzisen Resultaten führt. Diese Verschmelzung von KI und klassischer Mathematik eröffnet neue Perspektiven für die Computergrafik. Ein weiterer großer Vorteil der Methode ist ihre Universalität und Anpassungsfähigkeit. Sie ist nicht auf spezielle Formen oder Oberflächen beschränkt, sondern kann allgemein für verschiedenste implizite Funktionen angewandt werden.
Dies macht sie besonders attraktiv für Forscher und Entwickler, die mit unterschiedlichsten geometrischen Modellen arbeiten. Die genaue Erhaltung des Nullniveaus liefert insbesondere für Anwendungen, bei denen die exakte Grenzfläche eine wichtige Rolle spielt, entscheidende Vorteile. Beispiele hierfür sind Simulationen von physikalischen Phänomenen, bei denen Oberflächeninteraktionen relevant sind, oder in der Konstruktionsphase von 3D-Modellen. Fehler in der Lage des Nullniveaus könnten dort gravierende Auswirkungen auf das Ergebnis haben. Darüber hinaus trägt die Methode durch die Nutzung differenzierbarer neuronaler Netze dazu bei, dass sie in modernste Frameworks für maschinelles Lernen und Simulationssysteme leicht integrierbar ist.
Dies ebnet den Weg für automatisierte und optimierte Workflows im Bereich der Grafikgenerierung und -verarbeitung. Ein weiterer Aspekt von Bedeutung ist die methodische Eleganz des Verfahrens. Durch die Multiplikation des Netzwerkausgangs mit der gegebenen impliziten Funktion wird eine starke Bindung an die ursprüngliche Oberfläche hergestellt, was sich in präzisen und stabilen Ergebnissen niederschlägt. Gleichzeitig behält das Netzwerk genügend Freiheit, um die übrigen Eigenschaften der signierten Abstandsfunktion durch Training zu optimieren. Diese Entwicklung zeigt einmal mehr, wie framelozende neue Ansätze in der Wissenschaft für praktische Lösungen sorgen, die zuvor mit klassischen Methoden nur schwer oder unzureichend erreichbar waren.
Das hohe Potenzial dieser Technik lässt erwarten, dass in Zukunft weitere Anwendungen und Erweiterungen entstehen werden, die auf ihr aufbauen. Pierre-Alain Fayolles Beitrag markiert somit einen wichtigen Schritt in der effizienten und exakten Behandlung von SDFs im Bereich der Computergrafik. Die Veröffentlichung in einer Open-Access-Zeitschrift macht die Informationen breit zugänglich und fördert den wissenschaftlichen Austausch in der Community. Für Entwickler, Forscher und Interessierte bietet die Verfügbarkeit des vollständigen Artikels, Mustercodes und weiterer Materialien die Möglichkeit, die Technik selbst auszuprobieren, weiterzuentwickeln und in verschiedenste Projekte zu integrieren. Die Zukunft der Signierten Abstandsfunktionen kann dank solcher innovativen Ansätze eine präzise, flexible und auf neuronalen Netzwerken basierende Lösung sein, die alle Anforderungen moderner grafischer und numerischer Anwendungen erfüllt.
In Kombination mit den stetig zunehmenden Rechenkapazitäten und verbesserten Trainingsalgorithmen verspricht diese Methode nicht nur theoretisch überzeugende Ergebnisse, sondern auch eine praktische Umsetzung in industriellen und künstlerischen Kontexten. Letztendlich ist die exakte Erhaltung des Nullniveaus bei der Berechnung von signierten Abstandsfunktionen ein bedeutendes Qualitätsmerkmal, das die Grundlage für qualitativ hochwertige Darstellungen und Berechnungen moderner visueller Systeme bildet. Die hier beschriebene Technik besitzt das Potenzial, als Standardverfahren etabliert zu werden, das den Weg in eine neue Ära der präzisen Oberflächenmodellierung ebnet.