In der heutigen digitalen Welt, in der Personalisierung den Unterschied zwischen Erfolg und Misserfolg eines Online-Geschäfts ausmacht, ist die Fähigkeit, Nutzer möglichst individuell anzusprechen, von enormer Bedeutung. Eine besonders mächtige, dabei aber überraschend zugängliche Methode, um genau diese Herausforderung zu meistern, ist die lineare Regression. Während komplexe maschinelle Lernverfahren oft mit großem Aufwand und hohen Kosten verbunden sind, bietet die lineare Regression einen einfacheren Einstieg in die Welt der datengestützten Personalisierung und A/B-Test-Optimierung. Stellen Sie sich vor, Sie betreiben einen Online-Shop und stehen vor der Wahl, auf der Startseite entweder ein Bild eines Hundes oder einer Katze anzeigen zu lassen. Ein klassischer A/B-Test könnte zeigen, dass die Hundebild-Variante im Durchschnitt zu mehr Käufen führt.
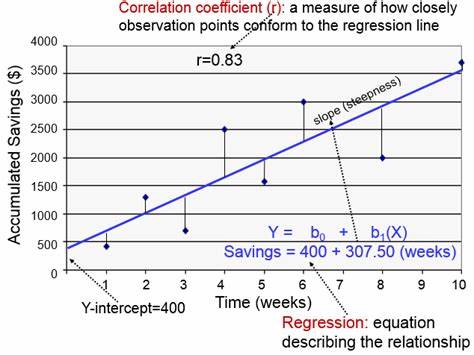
Einfach, oder? Doch solche pauschalen Ergebnisse unterschätzen häufig die Vielfalt der Besucher. Katzenliebhaber werden möglicherweise durch das Hundebild nicht angesprochen, obwohl sie einen wichtigen, wenn auch kleineren Kundensegment darstellen. Genau hier setzt die lineare Regression an, indem sie es ermöglicht, verschiedene Nutzergruppen individuell zu analysieren und zu bedienen. Grundlegend beruht die lineare Regression auf der Formel β = (X'X)⁻¹X'Y, eine Statistik-Gleichung, die uns erlaubt, den Zusammenhang zwischen einer Zielgröße, etwa dem Kaufverhalten (Y), und mehreren erklärenden Variablen, den Nutzermerkmalen (X), zu bestimmen. Die Betavektoren β geben dabei Aufschluss darüber, wie stark jede einzelne Eigenschaft das Ergebnis beeinflusst.
Durch die Aufspaltung der Daten in verschiedene Gruppen – beispielsweise Nutzer, die das Katzenbild sehen, und solche, die das Hundebild sehen – können Sie für jede Gruppe eigene β-Werte berechnen. Die Umsetzung ist, entgegen der anfänglichen Befürchtung wegen der Matrixtransponierungen und -inversionen, überraschend simpel. Ein entscheidender Schritt ist die Berechnung der sogenannten X'X-Matrix. Praktisch kann man sich das als eine erweiterte Pivot-Tabelle vorstellen, in der die Häufigkeiten von Wertekombinationen verschiedener Kategorien wie Betriebssystem und Browser miteinander kreuztabelliert werden. Dabei ist es wichtig, für die Variablen je eine Basiskategorie zu definieren und deren Zeilen sowie Spalten bei der Berechnung wegzulassen, um sogenannte „Dummy-Traps“ zu vermeiden – Probleme, welche die Berechnung der Regressionsparameter verfälschen könnten.
Das Invertieren der X'X-Matrix ist mathematisch gesehen der anspruchsvollste Teil, lässt sich jedoch mit bewährten Bibliotheken wie LAPACK leicht automatisieren. Moderne Softwarelösungen und Programmiersprachen bieten entsprechende Funktionen, sodass der Zeitaufwand und die Komplexität minimal sind. Nachdem die Inversion erfolgt ist, wird die Matrix mit der X'Y-Matrix multipliziert. Letztere entsteht aus der Summe der Verkäufe für jede Kategorie. Das Ergebnis ist der gesuchte Betavektor β, der genau angibt, wie jede Eigenschaft das Kaufverhalten beeinflusst.
Diese Methode bietet enorme Flexibilität. Statt eine Variante für alle Nutzer gleich zu zeigen, können Sie nun individuell berechnen, welche Bildversion für welchen Besucher am profitabelsten ist. Für einen Mac-Benutzer, der Firefox verwendet und sich als Katzenliebhaber eingestuft wird, kann das Katzenbild den Umsatz maximieren, während für einen Windows-Nutzer mit Chrome das Hundebild besser geeignet ist. Ein einfacher Vergleich der prognostizierten Erlöse für jede Variante entscheidet somit über die individuelle Anzeige. Ein weiterer Vorteil der linearen Regression ist ihre Skalierbarkeit.
Je nachdem, welche Variablen Sie berücksichtigen möchten – etwa Gerätekategorie, Standort, Besuchszeit oder vorheriges Kaufverhalten – lässt sich das Modell problemlos erweitern. Dadurch entsteht ein immer präziseres Bild der Kundenpräferenzen, ohne aufwendige Tests oder übertriebene Komplexität einzuführen. Die einzige Grenze ist die Rechenleistung bei sehr vielen Variablen, da die Matrixinversion mit wachsender Dimension aufwändiger wird. Neben der Optimierung von Personalisierung hilft die Analyse der Betavektoren auch dabei, weniger erfolgreiche Varianten eines Experiments zu erkennen und gegebenenfalls auszusortieren. Auf Basis der Differenz zwischen den β-Vektoren der verschiedenen Gruppen lässt sich feststellen, ob eine Variante in keinem Szenario wettbewerbsfähig ist.
Solche datengetriebenen Entscheidungen verhindern unnötige Ressourcenverschwendung und verbessern die Nutzererfahrung nachhaltig. Selbstverständlich stellt sich die Frage, ob Unterschiede zwischen Varianten statistisch signifikant sind. Für diese Analyse eignet sich der Chow-Test, der es erlaubt, die Gleichheit der Regressionskoeffizienten zwischen Gruppen zu überprüfen. Obwohl dessen Berechnung etwas komplexer ist, bieten viele statistische Softwarepakete fertige Funktionen dafür an. So können Sie Ihre Entscheidungen nicht nur auf Basis von Prognosen, sondern auch auf fundierten Wahrscheinlichkeiten treffen.
Das wirklich Bemerkenswerte an der linearen Regression für Personalisierung und A/B-Testing ist, dass sie mit relativ geringem technischem Aufwand umsetzbar ist. Sie benötigen keine ausgefeilten Machine-Learning-Systeme oder riesige Rechenzentren. Schon mit einfachen Werkzeugen und grundlegenden mathematischen Funktionen können Sie in kurzer Zeit ein leistungsstarkes Modell erstellen und direkt einsetzen. Dies ermöglicht auch kleineren Unternehmen, von den Prinzipien moderner Datenwissenschaft zu profitieren. Zudem ist die lineare Regression didaktisch wertvoll.
Sie stärkt das Verständnis für statistische Zusammenhänge und hilft dabei, anderen Teams – Marketing, Produktentwicklung oder Geschäftsleitung – die Wirkungsweise von Personalisierungsmaßnahmen transparent und nachvollziehbar zu erklären. Anders als Black-Box-Modelle öffnet sie den Blick für den Einfluss einzelner Merkmale und macht die Optimierung damit greifbar. In der Praxis beginnt der Einsatz der linearen Regression mit dem Sammeln und Aufbereiten der Daten. Achten Sie darauf, Nutzermerkmale sauber und eindeutig zu kategorisieren. Das können neben technischen Daten wie Browser und Betriebssystem auch demografische Informationen oder das Nutzerverhalten sein.
Wichtig ist, dass die Variablen möglichst wenig korreliert sind, um die Regressionsrechnung nicht zu verfälschen. Anschließend führen Sie die beschriebenen Schritte durch: Pivot-Tabellen erstellen, X'X-Matrix bilden, invertieren, X'Y summieren und schließlich die Betavektoren berechnen. Die Ergebnisse liefern Ihnen einen Maßstab, wie Nutzer unter unterschiedlichen Voraussetzungen reagieren werden. Die Umsetzung in eine Live-Personalisierung ist dann eine Frage der Integration in Ihre Webplattform, wo die entsprechenden Parameter je Nutzer dynamisch ausgewertet werden. Diese Methode verbindet statistische Genauigkeit mit praktischer Umsetzbarkeit und bietet eine enorme Hebelwirkung für Ihr Online-Geschäft.
Indem Sie nicht einfach nur Variationen A oder B anzeigen, sondern individuell für jeden Nutzer die passendste Variante ermitteln, steigern Sie die Zufriedenheit Ihrer Kunden und maximieren gleichzeitig Ihre Erlöse. Zusammenfassend ist die lineare Regression für die Personalisierung von Online-Angeboten eine effektive und effiziente Technik, die sich sowohl für Einsteiger als auch erfahrene Analysten eignet. Gerade im Umfeld immer anspruchsvollerer Kunden ist die Fähigkeit, auf individuelle Präferenzen einzugehen, ein entscheidender Wettbewerbsvorteil. Durch simpel anwendbare Mathematik lassen sich große Datenmengen in wertvolle Erkenntnisse verwandeln, die unmittelbar in besseren Geschäftsergebnissen münden. Wer die Grundlagen verstanden und erste Modelle implementiert hat, wird schnell feststellen, dass die Investition in diese Methode sich mehrfach auszahlt – durch höhere Conversion-Raten, geringere Absprungraten und letztlich auch durch ein besseres Verständnis der eigenen Kundschaft.
Insbesondere kleine und mittlere Unternehmen profitieren von der Praktikabilität der linearen Regression und ihrer Fähigkeit, ohne großen Aufwand datengetriebene Entscheidungen zu treffen. Abschließend lädt die lineare Regression dazu ein, datenbasierte Personalisierung nicht als technische Hürde, sondern als lösbare Herausforderung zu begreifen. Von A/B-Tests über Segmentierung bis hin zu Prognosen von Nutzerverhalten bietet sie einen vielseitigen Werkzeugkasten für nachhaltigen Online-Erfolg. Nutzen Sie diese Methode, um Ihre Website intelligenter zu gestalten, Kunden individueller anzusprechen und am Ende deutlich mehr aus Ihren Daten herauszuholen.