Im Bereich des maschinellen Lernens und der neuronalen Netzwerke stellt der Umgang mit diskreten Daten eine beträchtliche Herausforderung dar. Besonders bei catgorischen Verteilungen, welche aus einer endlichen Menge von Kategorien bestehen, ergeben sich Schwierigkeiten bei der Optimierung von Modellen, die auf diskreten Stichproben basieren. Die Gumbel-Softmax-Verteilung hat sich als eleganter Ansatz etabliert, dieses Problem zu lösen, indem sie eine differenzierbare Approximation diskreter Proben ermöglicht und somit eine nahtlose Integration in gradientenbasierte Lernverfahren erlaubt. In diesem Beitrag werden wir tief in die Konzepte, mathematischen Grundlagen und praktischen Anwendungen der Gumbel-Softmax-Verteilung eintauchen. Dabei betrachten wir sowohl den theoretischen Hintergrund als auch die konkreten Vorteile für moderne Machine-Learning-Architekturen.
Zunächst muss man verstehen, warum die Arbeit mit diskreten Wahrscheinlichkeitsverteilungen im Kontext von neuronalen Netzwerken so schwerfällt. Eine kategoriale Verteilung beschreibt Wahrscheinlichkeiten über diskrete Klassen, wie beispielsweise die Wahl zwischen verschiedenen Molekültypen beim Generieren von Graphstrukturen in der Chemie oder Entscheidungen über Kategorien in textbasierten Modellen. Jedoch ist es für neuronale Netzwerke essenziell, dass sämtliche Operationen differenzierbar sind, um die Gradienten mittels Backpropagation berechnen und das Modell entsprechend anpassen zu können. Diskrete Stichproben hingegen führen zu nicht-differenzierbaren Operationen, wie zum Beispiel zum argmax-Operator, da dieser keine kontinuierlichen Verläufe besitzt. Dies macht eine direkte Optimierung der Netzwerke schwierig oder gar unmöglich.
Die Idee, die hinter der Gumbel-Softmax-Verteilung steckt, ist es daher, diskrete Wahrscheinlichkeiten durch eine differenzierbare Funktion zu approximieren, die sich in das Trainingsverfahren integrieren lässt und die erforderlichen Gradienten zuverlässig liefert. Die Grundlage dieses Ansatzes entstand durch eine Kombination von zwei wichtigen Tricks: dem Reparameterization Trick und dem Gumbel-Max Trick. Der Reparameterization Trick wurde zuerst für kontinuierliche Verteilungen wie die Normalverteilung eingesetzt, um die Stochastizität der Sampling-Prozesse zu entkoppeln. Statt direkt von einer Zufallsvariable zu sampeln, lässt sich das Sampling als deterministische Funktion kombiniert mit einer stochastischen Eingangsgröße darstellen. Dies bedeutet, dass man die stochastischen und deterministischen Komponenten so trennt, dass sich die Ableitung nur über die deterministische Komponente berechnet.
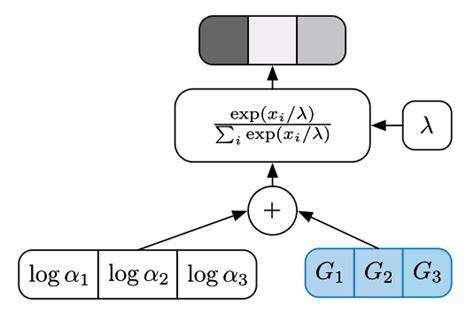
Die Anwendung auf diskrete Verteilungen erfordert jedoch eine Erweiterung, denn dort handelt es sich nicht mehr um kontinuierliche Wahrscheinlichkeiten. Hier kommt der Gumbel-Max Trick ins Spiel. Er ermöglicht die Probenziehung aus einer kategorialen Verteilung indem eine spezielle Art von „Gumbel-Rauschen“ zu den Log-Wahrscheinlichkeiten jeder Kategorie hinzuaddiert wird. Anschließend bestimmt die argmax-Funktion die für die Wahl relevante Kategorie. Die Gumbel-Verteilung wird in der Statistik häufig für die Modellierung von Extremwerten, also Maximal- oder Minimalwerten, verwendet.
Ihr Einsatz im Sampling-Prozess ist deshalb sinnvoll, da das Maximum über die Verteilungen gerade mit dieser Verteilung mathematisch gut repräsentiert werden kann. Der Nachteil des Gumbel-Max Tricks liegt darin, dass die argmax-Operation nicht differenzierbar ist. Hier setzt die Gumbel-Softmax-Verteilung an, indem sie die harte Auswahl (argmax) durch eine weiche Auswahl mittels der Softmax-Funktion ersetzt, die über die mit Gumbel-Rauschen versehenen Log-Wahrscheinlichkeiten angewandt wird. Die Softmax-Funktion ist kontinuierlich und differenzierbar, was eine wichtige Voraussetzung für die Anwendung in neuronalen Netzwerken ist. Die Gumbel-Softmax-Verteilung enthält zusätzlich einen Temperaturparameter, der das Verhalten der Verteilung steuert.
Mit hohen Temperaturen ähnelt die Verteilung eher einer glatten Wahrscheinlichkeitsverteilung, bei niedrigeren Temperaturen nähert sie sich immer mehr einer harten kategorialen Verteilung an, bei der eine einzelne Kategorie nahezu sicher ausgewählt wird. Dieser Temperaturparameter erlaubt eine stufenweise Annealing-Strategie während des Trainingsprozesses. Das bedeutet, dass das Modell zunächst mit einer hohen Temperatur trainiert wird, um stabile und robuste Lernschritte zu ermöglichen. Im weiteren Verlauf wird die Temperatur gesenkt, wodurch die Ausgabe der Gumbel-Softmax-Verteilung näher an eine echte diskrete Auswahl heranrückt. Dieser Ansatz balanciert das Spannungsfeld zwischen Lernstabilität und Genauigkeit optimal aus.
Die praktische Relevanz der Gumbel-Softmax-Verteilung ist enorm. Sie ermöglicht es beispielsweise, diskrete Entscheidungen innerhalb von Variational Autoencodern zu treffen, ohne die Gefahr des Abbruchs des Gradientenflusses. Ebenfalls bieten sich neuartige Generative Adversarial Networks (GANs) für diskrete Daten an. Für die molekulare Strukturentwicklung, Sprachmodellierung oder Bildklassifikation kann die Fähigkeit, diskrete Wahrscheinlichkeiten differenzierbar zu approximieren, immense Vorteile bringen. Zahlreiche Forschungsarbeiten und Anwendungen bestätigen den Erfolg dieser Methode.
Zudem erleichtert die Gumbel-Softmax-Verteilung die Umsetzung von Modellen, die auf diskreten Variablen basieren, erheblich, da klassische sampling-basierte Methoden kompliziert und ineffizient sein können. Im Hinblick auf die mathematischen Grundlagen sei erwähnt, dass die Gumbel-Softmax-Verteilung auch als eine spezielle Art der Concrete Distribution beschrieben wird, wie von Maddison et al. eingeführt. In beiden Arbeiten wird belegt, dass diese kontinuierliche Relaxation diskreter Wahrscheinlichkeitsverteilungen sehr gut funktioniert und zuverlässig Gradienten liefert, um effizientes Lernen zu ermöglichen. Die geometrische Interpretation spielt ebenfalls eine Rolle bei der intuitiven Verständlichkeit.
Die Wahrscheinlichkeitsvektoren der kategorialen Verteilung liegen auf einem sogenannten Simplex – man kann diesen als eine Verallgemeinerung eines Dreiecks in höherdimensionalen Räumen begreifen, wo die Eckpunkte den reinen Kategorien entsprechen. Durch das Modulieren der Temperatur werden die Wahrscheinlichkeiten von den Ecken dieses Simplex zu inneren Punkten verschoben, was die kontinuierliche Variation der Verteilung illustriert. Insgesamt stellt die Gumbel-Softmax-Verteilung eine bedeutende Errungenschaft im Deep Learning dar, die ein fundamentales Problem der Modellierung diskreter Wahrscheinlichkeiten im Kontext differenzierbarer Modelle löst. Sie hat die Tür geöffnet für neue Architekturen und Anwendungen, die bislang durch den Mangel an geeigneten Optimierungstechniken limitiert waren. Ihre Entwicklung zeigt eindrucksvoll, wie theoretische Konzepte aus der Wahrscheinlichkeitstheorie und Statistik in praktischer KI-Forschung zu bedeutenden Fortschritten führen können.
Wer sich intensiver mit dem Thema auseinandersetzt, wird erkennen, dass das Verständnis der Gumbel-Softmax-Verteilung nicht nur für wissenschaftliches Arbeiten relevant ist, sondern auch für praktische Implementierungen im Bereich des maschinellen Lernens unabdingbar wird. Die Kombination von mathematischem Tiefgang und algorithmischer Anwendbarkeit macht den Wert dieser Methode aus und wird sie in Zukunft sicher noch weiter etablieren.